J.Wheelerの遅延選択実験

• 前置き
  • 科学で扱える現象の範囲
  • オッカムの剃刀
• 実験概要
• 珍妙な仮定を持ち出す人たち
  • 前提の破綻
  • そもそもの勘違い
  • 実験との整合性
• 実験の真相
• まとめ
  • 通俗説
  • 物理学者の見解
• 参考

前置き 

当サイトの科学項目の目的も参照のこと。

科学で扱える現象の範囲 

科学で扱うためには、同じ条件では同じ現象になる(同じ数式で記述できる)ことが必須の前提となる。 その前提が崩れれば、科学法則が成立しないし、実験の再現性も失われる。 よって、科学法則を見出したり、実験で結果を確かめるためには、この前提が崩れてはならない。 言い換えると、同じ現象にならない(同じ数式で記述できない)ケースを科学で扱うためには両者には違う条件が必要となる。 尚、量子力学は確率的に結果を推定する理論であるので、ここで言う「現象」には確率も含む。

オッカムの剃刀 

実験結果を説明するために不要な仮定は置かない。 必要のない仮定を置いても、理論的考察の役にたたない。 無駄に話を難しくすれば、間違いを生みやすくなる。 メリットが全くなく、かつ、デメリットしかない不要な仮定は可能な限り排除すべきだろう。

実験概要 

以下は、大物物理学者のJ. Wheelerが提唱した実験である。 マッハ・ツェンダー干渉計の原理を応用して、次の(a)と(b)の光の干渉実験のセットを用意する。 BS1/BS2はハーフミラー（ビームスプリッター）であり、D1/D2は検出器である。

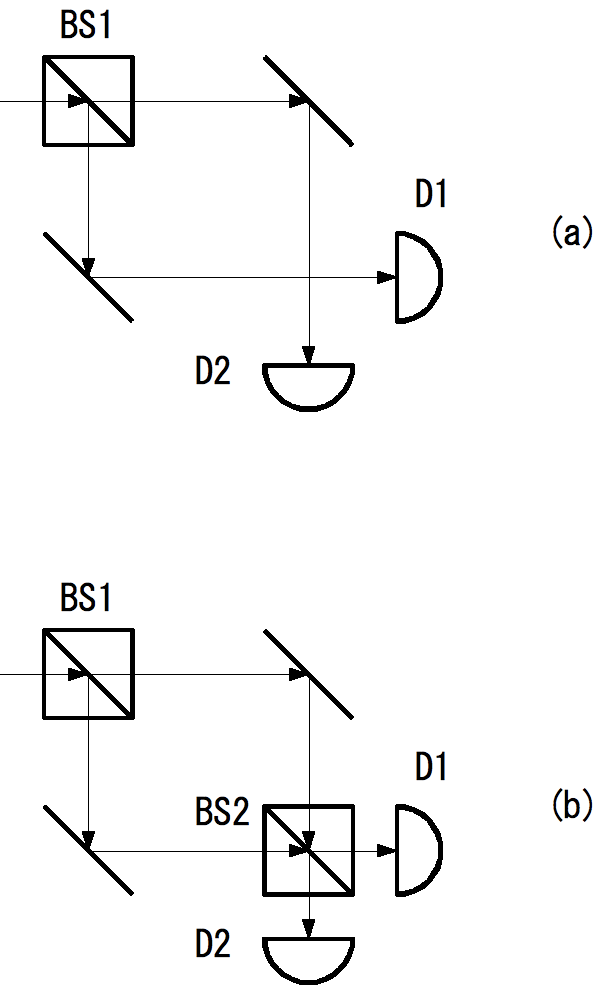
(a)と(b)の違いはBS2があるかないかだけである。 レーザー光が光源として使われ、光が検出器に到達するまでの時間のエネルギー量が量子１単位以下になるように調整されている。 D1では両経路の位相が逆相になり、かつ、D2では両経路の位相が同相になるよう、経路長が調整されている。 結果、次のようになる。

• (a)では、D1とD2の検出確率は半々
• (b)では、D1では検出されず、D2の検出確率が100%

BS1で２経路に分かれた光が再び交錯する所((b)でBS2がある所)までの経路(以下、「再交錯前経路」)において光に波動性があるのかどうか。 まず、再交錯前経路において波動性がある場合を考える。 (a)では、２つの経路を通った波が、それぞれ別々の検出器に到達するため、波の干渉が生じない。 その結果、D1とD2の検出確率は半々となる。 これは実験結果と一致する。 (b)では、２つの経路を通った波が、それぞれBS2で半分ずつに分けられ、それぞれの合成波がD1とD2に到達する。 D1では合成された波が打ち消しあうので、D2でしか光を検出できない。 その結果、D1では検出されず、D2の検出確率が100%となる。 これも実験結果と一致する。 以上の通り、再交錯前経路において波動性がある場合は(a)も(b)も実験結果と一致する。

次に、再交錯前経路において波動性がない場合を考える。 (a)では、上下の経路を半々の確率で通過することになる。 結果、D1とD2の検出確率は半々となる。 これは実験結果と一致する。 (b)でも、上下の経路を半々の確率で通過することになる。 そして、BS2を通過または透過する確率も、半々である。 結果、D1とD2の検出確率は半々となる。 これは実験結果と一致しない。 以上の通り、再交錯前経路において波動性がない場合は(b)だけが実験結果と一致しない。

• (a)の最終結果は、再交錯前経路において波動性があってもなくても説明できる
• (b)の最終結果は、再交錯前経路において波動性がないと説明できない

尚、(a)と(b)の条件は同じなので、再交錯前経路における現象は、当然、同じ現象になると推定する。 であれば、この実験結果を説明するには、(a)(b)いずれにおいても再交錯前経路の波動性が必要である。 何故なら、(a)(b)双方に再交錯前経路の波動性がない場合は、(b)の結果が説明できないからである。 逆に、再交錯前経路の波動性があれば、(a)(b)いずれの結果も矛盾なく説明できる。

さて、では、光がBS1を通過した後に、BS2を置くかどうかを決めるとどうなるか。 実際には、ビームスプリッターを高速で出し入れするのは難しいので、高速シャッター（オプティカルチョッパー）を用いて等価的装置を構成している。

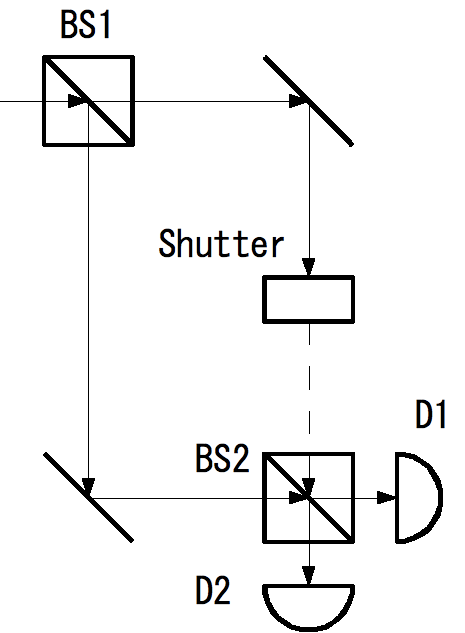
シャッターを閉じると、BS2には下の経路の光しか通らないが、BS2はハーフミラーであるのでD1とD2の検出確率は半々となる。 シャッターを開くと、BS2には両方の経路の光が通り、かつ、波の干渉により、D2でしか光を検出されない。 つまり、シャッターを閉じた場合は(a)と同じ結果が得られ、シャッターを開いた場合は(b)と同じ結果が得られるのであり、実験結果には何も変化はない。

以上の結果は波動性と粒子性の二重性と確率解釈で何の問題もなく説明できる。

珍妙な仮定を持ち出す人たち 

どういうわけか、次のような珍妙な仮定を持ち出す人がいる。

• (a)では、再交錯前経路において一方の経路を波動性のない粒子が通過する
• (b)では、再交錯前経路において両方の経路を粒子性のない波が通過する

何故、再交錯前経路においては全く同じ条件なのに違う現象と考えるのか、その理由は全く提示されない。 そして、同じ現象であると推定しても実験結果を説明するうえで何の不都合もない。 一般的な推定の原則に照らしても、実験結果に照らしても、違う現象と考える理由はどこにもない。 にも関わらず、再交錯前経路においては全く同じ条件なのに違う現象とする仮定を置くのは何故か。 その理由は全く提示されない。

前提の破綻 

確かに、次の前提条件が全て成立する場合、(a)では再交錯前経路において波動性を失うと考える必要が生じる。

• 粒子性がなければ検出器は反応しない
• 波動性と粒子性は排他的である(ある瞬間にはどちらかの性質しか示さない)
• 検出器では粒子性が生じない
• 何もない空間でも粒子性が生じない

逆に、このうちの条件がひとつでも崩れれば、再交錯前経路において波動性を失うと考える必要は生じない。 粒子性がなくても検出器が反応するか、あるいは、波動性と粒子性が両立するのであれば、波動性を維持していても検出器は反応するはずである。 検出器や何もない空間で粒子性が生じるなら、光が再び交錯する所((b)でBS2がある所)以降(以下、「再交錯後」)に波動性を失っても十分に間に合うから、再交錯前経路において波動性を失うと考える必要はない。 よって、何れの条件が崩れても、再交錯前経路において波動性を失うと考える必要性が失われる。

一方で、これらの条件を全て満足するためには、(a)(b)いずれにおいても、再交錯後に波動性を失っている必要がある。 その場合、(b)では、再交錯後の波の干渉が生じなくなり、実験結果を説明できなくなる。 以上の通り、(a)の再交錯前経路において波動性を失うとの仮定は、(b)の実験結果と矛盾しており、その前提から破綻している。

そもそもの勘違い 

「確率が50%ずつとなることが波動性では説明できない」と思うなら、それは間違いである。 それを説明するための確率解釈である。 確率解釈を否定すれば、(b)の検出確率も説明できない。 逆に、確率解釈を採用すれば、どちらの結果も問題なく説明できる。 例えば、【1ns毎に光子1個相当】の場合を考える。 その場合、(b)のD2における、ある0.5ns間と次の0.5ns間の検出確率は50%ずつとなる。 「確率が50%ずつとなることが波動性では説明できない」なら、この結果も波動性では説明できなくなる。 言うまでもなく、波動性がないと干渉は説明できない。 よって、この場合、光子の検出と干渉が両立できなくなるため、(b)の実験結果が説明できなくなる。 そもそも、(b)のD2においても、常に1個の光子が検出されるわけではない。 例えば、【1ns毎に光子1個相当】の場合も、キッチリ1ns間隔で光子を送出しているわけではない。 あくまで、1ns間の送出エネルギー量が光子1個分に等しいだけである。 光子を1個単位で選り分けることはできないので、キッチリ1ns間隔で光子を送出する実験は不可能である。 だから、ある1ns間では2個の光子が検出されることもあるし、別の1ns間では1個も光子が検出されないこともある。 平均確率が100%になるだけであって、常に1個の光子が検出されることは保証されない。 このような現象が波動性で説明できないなら、光子の検出と干渉が両立できなくなるため、(b)の実験結果が説明できなくなる。 逆に、(b)の実験結果が波動性で説明できるなら、(a)の実験結果も波動性で説明できるはずである。

実験との整合性 

さて、この珍妙な仮定においては、高速シャッターを用いる場合に当てはめると次のようになる。

• シャッターを閉じた場合は、再交錯前経路において一方の経路を波動性のない粒子が通過する
• シャッターを開いた場合では、再交錯前経路において両方の経路を粒子性のない波が通過する

この仮定では、BS1通過時にはシャッターを閉じておいて、BS1通過後からシャッター到達前までにシャッターを開けると、再交錯前経路において一方の経路を波動性のない粒子が通過するため、D1とD2の検出確率は半々となるはずである。 しかし、実際の実験では、この場合はD2でしか光を検出していない。 この矛盾する結果に対して、最初の仮定を持ち出した人は、未来が過去を決める証拠だなどと言い出す。 正常な思考力を持つ人なら、全く意味がわからないだろう。 ある仮定で実験結果が説明できないなら、真っ先に、その仮定が間違いではないかと疑うのが科学的な姿勢である。 仮定を検証することなく、さらに突拍子もない仮定を追加するのでは、疑似科学の典型的な事例である。

実験の真相 

Wheeler「光子がスリットを通過した後に光源を置くかどうか(すなわち、波動性と粒子性のどちらを観測するか)の選択を行ったとしたらどうなるだろうか?」

もしこれまでと同じように、光源があった時に粒子性を示し、光源が無い時に波動性を示せば、スリットを通過した時点ではどちらの状態か決まっていないことが言える。

つまり、波動性も粒子性も一光子に共存しているという事が言える！？

大阪大学大学院 久野・山中研究室合同発表資料

これによると、測定の仕方が量子の波の性質に影響を及ぼすかどうかを調べようとしたようだ。 具体的に言い替えると、二重スリット実験を分かりやすく説明で説明した二重スリット実験で粒子がどちらのスリットを通過したか調べると干渉縞が発生しなく原因について、次のどちらによるのかを調べようとしたようだ。

• どちらのスリットを通過したか調べることで量子が波の性質を失う
• 波の性質を保持しているが、それとは別の原因で干渉縞が消える

波の性質を失うことによって干渉が発生しなくなるのならば、スリット（この実験では１つ目のビームスプリッターに相当）を通過する段階で波の性質を失っていなければおかしい…………本当に？ 干渉領域より遙か手前で波の性質を確認できても、干渉領域に達した段階で波の性質を保持している証拠にはならないはずである。 それはともかく、次のような実験を行なえば、１つ目のビームスプリッターを通過した時点で波の性質を保持しているかどうかは確認できる。

1. 最初は、２つ目のビームスプリッターを抜いておいておいて、粒子性を測定する装置にしておく。
2. 光が１つ目のビームスプリッターを通過した後、再交錯する所に到達する前に、２つ目のビームスプリッターを入れて、波動性を測定する装置に切り替える。
3. これで干渉が発生すれば、粒子性を測定しようとしても、最初のビームスプリッターを通過するときに波の性質を持っている。

つまり、１つ目のビームスプリッターを通過した段階で波の性質を保持しているかどうかという物理現象より後に、測定の仕方を「遅延」選択しているのだ。 実際には、ビームスプリッターを高速で出し入れするのは難しいので、高速シャッター（オプティカルチョッパー）を用いて等価的装置を構成している。

これにより、どのように測定しようとしても、１つ目のビームスプリッターを通過した段階で波の性質を保持していることは確認された。 少なくとも「波を測定しようとしたか、粒子を測定しようとしたかに関係なく、経路が別れた直後は波としての性質を維持している」とは言えるだろう。 しかし、測定の仕方が量子の波の性質に影響を及ぼさない（もっと厳密に言うと、量子は、その時々で、波になったり粒子になったりするのではなく、波としての性質と粒子としての性質が一体不可分の物と表現すべきだろうか）ことが確認された……………と言えるのだろうか？

まとめ 

通俗説 

分かりやすい二重スリット実験の説明で説明した二重スリット実験のスリットを通過した後は次のいずれかになると主張する人がいる。

• 経路を特定しようとすると波動性のない粒子になる
• 経路を特定しないと（粒子性のない）波になる

もちろん、このように考える合理的理由は何もない。 しかし、何故か、彼らはこのような珍妙な仮定を採用する。 この仮定で遅延選択実験を行うと、最初のビームスプリッター（二重スリット実験のスリットに相当）を通過する時点では経路を特定するセットにするか、特定しないセットにするか、未だいずれかを選択していないにも関わらず、次のような結果となる。

• 経路を特定しようしても、しなくても、最終的かつ結果的に経路を特定するセットになっていれば、波動性の有無は不明で粒子性のみ観測される
• 経路を特定しようしても、しなくても、最終的かつ結果的に経路を特定しないセットになっていれば、二つの経路を通過する波動性＝干渉（と粒子性）が観測される

最初の仮定を採用すると、この実験結果は、説明が困難である。 しかし、彼らは、未来の選択に合わせて量子が粒子になったり波になったりすると主張する。 つまり、珍妙な仮定に更なる珍妙な仮定を重ねて、この結果が未来が過去を決める証拠だと言う。

物理学者の見解 

大阪大学大学院の久野・山中研究室合同年末発表会によれば、Wheelerは次のいずれが正しいかを検証しようとした。

• スリットを通過した後は次のいずれかになる
  • 通過スリットを特定しようとすると波動性のない粒子になる
  • 通過スリットを特定しないと（粒子性のない）波になる
• 通過スリットを特定しようとするかどうかによる変化はない（波動性と粒子性を併せ持つ）

実験を行うと、最初のビームスプリッター（二重スリット実験のスリット）を通過する時点では経路を特定するセットにするか、特定しないセットにするか、未だいずれかを選択していないにも関わらず、次のような結果となる。

• 経路を特定しようしても、しなくても、最終的かつ結果的に経路を特定するセットになっていれば、波動性の有無は不明で粒子性のみ観測される
• 経路を特定しようしても、しなくても、最終的かつ結果的に経路を特定しないセットになっていれば、二つの経路を通過する波動性＝干渉（と粒子性）が観測される

前者の仮定を採用すると、この実験結果は、説明が困難である。 よって、前者の仮定は間違いで、後者の仮定が正しいと推測される。

この実験結果から確実に言えることは、Dr.Quantumによる二重スリット実験トンデモ解説とは違い、量子の「振る舞い」は「自分が見られている」かどうかによって変化しないということである。 つまり、「まるで、自分が見られていることに気づいたかのように」「観測された電子は、観測される前とは違う振る舞いをした」は遅延選択実験の結果と整合しない。 あまりにもバカバカしい珍説を敢えて検証し、当然予想される通りその珍説が正しくないことを証明したという以上の意味はないようである。

具体的トンデモ論については遅延選択実験トンデモ解説で紹介する。

参考 

• 遅延選択量子消しゴム実験