観測問題

• 概要
• 広義の観測問題
• 狭義の観測問題

概要 

観測問題とは、平たく言えば、波動性と粒子性の二重性の整合を取ろうとしたときに立ちはだかる問題。 波的な性質についてはシュレーディンガー方程式に従う波動関数で記述できる。 しかし、粒子的な性質はそれだけでは記述できない。 波動関数から確率的に導くことはできるが、確定的な値は導けない。

広義の観測問題 

量子力学において観測が問題になると言われるとき，関連するのは次の３つの条件である．

(Ａ)固有値⇆固有状態リンク

(Ｂ)孤立系のシュレーディンガー方程式にしたがう状態変化

(Ｃ)測定が行われると測定値が得られるという経験的事実

条件(Ａ)は状態と性質を結びつけるひとつの見解として，わざわざ明示されないほど自明な事柄として初期の量子論から広く物理学者に採用されているものであり，条件(Ｂ)は量子力学の基本原理として理論に組み込まれている． 条件(Ｃ)は量子力学とは独立しているが，むしろ経験科学が成立するための共通認識として前提されるべき事柄であろう． ところが，この3つの条件はお互いに整合的ではないのである．

---

３つの条件(Ａ)，(Ｂ)，(Ｃ)はそれぞれ重要であり，じつのところどの２つの組み合わせも整合的であるのだが，３つを同時に仮定することはできない． 本章では，この困難をいかにして克服するかという問題が，いわゆる「量子力学の観測問題」の核心であるという立場で議論を進めていくことにしよう．

「量子という謎」(ISBN-10:4326700750,ISBN-13:978-4326700752,著:白井仁人・東克明・森田邦久・渡部鉄兵)P.7,8

補足すると、条件(Ａ)は波動関数の計算値(固有状態)と可観測量(固有値)が一対一で対応していることを意味している。 ３つの条件(Ａ)，(Ｂ)，(Ｃ)が全て成立すると仮定すると、計算上は値が確定しないにも関わらず、測定値は確定しているという矛盾が生じてしまう。 「３つを同時に仮定することはできない」とは、そういうことである。

条件(Ｂ)，を否定する，とりわけ射影公準によるもうひとつの状態変化を認めると，条件(Ａ)，(Ｃ)と整合的となり，本章で定式化した観測問題は解消される．

「量子という謎」(ISBN-10:4326700750,ISBN-13:978-4326700752,著:白井仁人・東克明・森田邦久・渡部鉄兵)P.12

条件(Ａ)の否定は、いわゆる隠れた変数理論である。 標準理論では、条件(Ｂ)を否定する射影公準(射影仮説)を採用し、観測に伴って波動関数の収縮が起こるとしている。

狭義の観測問題 

しかし，射影公準の主張する波束の収束はいつ起きているのか． いいかえれば，射影公準で述べられている「測定後」とはいつの時点を指しているのだろうか．

「量子という謎」(ISBN-10:4326700750,ISBN-13:978-4326700752,著:白井仁人・東克明・森田邦久・渡部鉄兵)P.12

射影公準(射影仮説)における「観測」を明確に定義するのは困難である。

射影仮説は,量子論が,実験事実と合致しかつ無矛盾な理論体系になるために必要であるからこそ導入された公理なのである.

---

射影仮説には,次の2つの役割がある:
(A)異なる測定値に対応する状態ベクトルの間の干渉をなくす
(B)干渉の無くなった2つの状態ベクトルのうちのどちらかを抜き出す

---

要するに,どちらか定まらないものから,どちらか一方だけを選び取るためには,いつも定まった値をとるようなダイナミックスに従うものが必要なのである. しかるに,この世界の全てが量子論のユニタリー時間発展に従うと考えると,そのような,常に定まった値をとるダイナミックスに従うものが存在しなくなってしまうので,困るのである. 射影仮説は,このやっかいな問題を断ち切る役割も担っているのだ.

量子測定の原理とその問題点 by 東京大学大学院総合文化研究科広域科学専攻相関基礎科学系＆東京大学大学院理学系研究科物理学専攻：清水明教授

射影仮説は「実験事実と合致しかつ無矛盾な理論体系になるために必要」で、「どちらか定まらないものから,どちらか一方だけを選び取る」。 これは、言い替えると、「実験事実と合致しかつ無矛盾な理論体系になるため」には、「どちらか定まらないものから,どちらか一方だけを選び取る」ことが必要であることを意味する。 そして、「この世界の全てが量子論のユニタリー時間発展に従うと考える」と「どちらか定まらないものから,どちらか一方だけを選び取る」のに必要な「常に定まった値をとるダイナミックスに従うもの」がなくなるなら、「この世界の全てが量子論のユニタリー時間発展に従うと考える」と「実験事実と合致しかつ無矛盾な理論体系」になっていない。 つまり、「常に定まった値をとるダイナミックスに従うもの」を仮定して、射影仮説を適用しないと「このやっかいな問題を断ち切る」ことはできない。 しかし、では、その「常に定まった値をとるダイナミックスに従うもの」とは一体何なのか？ 量子力学の理論では、「観測」「測定」と呼称されるが、それが何なのかは明確に定義されていない。

「観測」の定義の困難さはシュレーディンガーの猫の思考実験が的確に表しているとされる。 しかし、マクロと相互作用する段階で可観測量が確定すれば、この問題はあっさりと解決する。 理想測定であれば、量子測定理論の知見により、Heisenberg cutで遮断して射影仮説を適用できる。

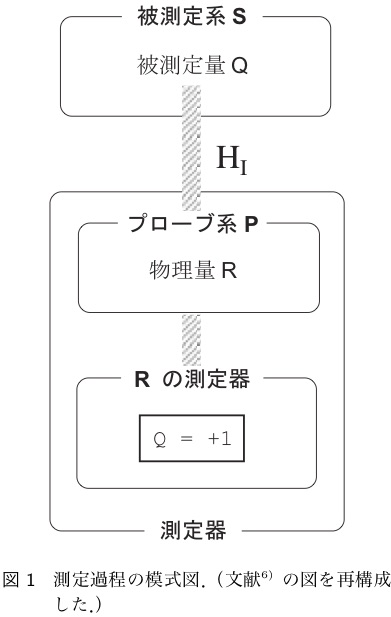
図1のように，被測定系Sのある物理量Qを測る場合，Sを測定器の一部(プローブ系Pと呼ぶことにする)と相互作用させ，Qの情報を，Pのある物理量Rに「コピー」してくる. ここで，「コピー」と言ったのは，Qの値とRの値が相関するようにする，という意味であり，そっくり写し取るなら理想的だが，そうでなくても，何か関連付けば良い. そして，測定器の中には，このRの値を測る部分が付いている.Rの値は，Qの値と相関しているので，このRの値からQの値を推定することができる. その推定の仕方は，測定器の構造により決まるが，Rの測定値から，その推定のルールにのっとって求めたQの推定値を，ディスプレイとか目盛りとかに表示するのが測定器の動作原理である.

このように分解して考えると，Rを測る過程は理想測定と見なせるので，射影仮説が使える.(逆に言えば，公理より，理想測定と見なせる過程が存在するので，Rの測定が理想測定になるようにPを選ぶ!) つまり，理想測定と見なせる境目までは，量子論に従う系の一部として扱い，そこから先を考えることは，射影仮説により遮断する. それが，一般の測定過程の分析の仕方の処方箋である. この境目(「Heisenberg cut」と呼ばれる)の位置には任意性があるが，先の方にずらす分には，まったく同じ結果を与えるので，要するに，充分に大きな系を量子論に従う系として扱っておけば，結果には任意性は出ないのである.

量子測定の原理とその問題点 by 東京大学大学院総合文化研究科広域科学専攻相関基礎科学系＆東京大学大学院理学系研究科物理学専攻：清水明教授

---

どの系にこれらを適用するかが問題なのです。

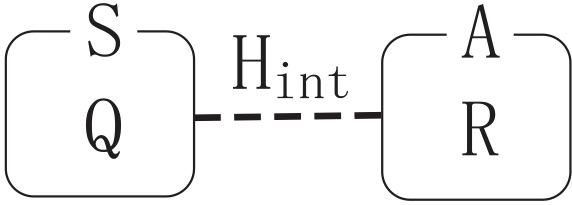
どこに適用するかで大きな違い(R. J. Glauber, 1963)

• 被測定系Sに対して適用したのでは、実験と合わない場合がある
• Sと測定器Aの合成系に対して適用すれば、実験と合う整合した理論に なる
• そうすれば、測定器の誤差や測定の反作用も、きちんと計算できる

→R. J. Glauberが現代的な量子測定理論の扉を開いた(1963)

---

SとAの合成系をひとつの量子系として扱い「メーター変数」Rを測る

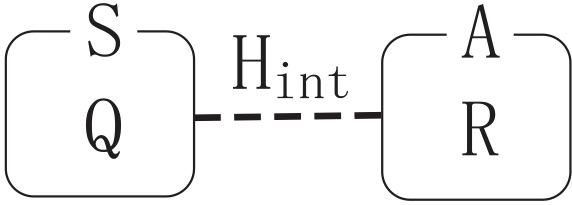
1. SとAの相互作用により、合成系の状態が変わる→シュレディンガー方程式を合成系に適用
   • RとQの間に相関がある状態になる
2. その状態の、QではなくRを、別の測定器(または観測者)で測る
   • 射影仮説を合成系の状態に適用(射影演算子はPˆQ(q)ではなくPˆR(r))
   • 測定後の状態が定まる(測定の反作用が求まる)
3. Rの測定値rから、Qの値qを推定する
   • 有限の誤差が出る(測定誤差の大きさが求まる)

---

考えてみると、次のようになっているわけです:

A′は、別の測定器でもいいし、観測者の目でもいい。 このような構造を、von Neumann chainと呼びます。

量子論を使うときには、どこかに境目(Heisenberg cut)を設けて、

• その左側を量子系として、量子論の諸原理を適用する
• 右側は、左側に対する理想測定を行うデバイス

とするわけです。

---

von Neumannはこの性質を、psychophysical parallelismと呼びました。

結局、ある所にHeisenberg cutを設けることができる(その右側が左側に対する 理想測定を行うと見なせる)ならば、

• cutの位置を、それよりも右側に移動することはできる
• 左側に移動するのは、できるとは限らない

Modern Theory of Quantum Measurement and its Applications by 東京大学大学院総合文化研究科広域科学専攻相関基礎科学系＆東京大学大学院理学系研究科物理学専攻：清水明教授

測定する側は、測定される側に一定の影響を与える。 これを避ける方法はない。 しかし、測定される側がマクロの物質で量子力学的性質が極めて弱い場合、測定する側から受ける影響は極めて小さい。 その場合は、測定する側と測定される側の境界にHeisenberg cutを設定できる。 Heisenberg cutより観測者に近い側が測定結果に与える影響は無視して差し支えない。 ようするに、Heisenberg cutより測定対象側だけで測定結果が決まると見なして差し支えない。 つまり、観測者の意識を特別視するまでもなく、測定対象(と測定器の一部)だけで結果が確定するのである。 この思考実験についても、量子測定理論では次のように解釈される。

以上のことから，射影公準によれば，波束の収束は放射性物質とガイガーカウンター（の一部）の相互作用が終了する時刻にはすでに起こっており，この時刻で猫の運命は決まる． この観点からは，巨視的な猫の状態がどのように変化するのかは，測定終了後にどのような増幅過程が進行するのかという技術的な事柄にすぎない．

「量子という謎」(ISBN-10:4326700750,ISBN-13:978-4326700752,著:白井仁人・東克明・森田邦久・渡部鉄兵)P.15

この場合、測定される側だけで、結果が決まっていると見なして差し支えない。 つまり、検出器がα粒子を検出した段階で、猫の生死が確定すると考えられる。 測定される側は、測定する側の影響をほとんど受けないのだから、当然、観察者の意識の影響を受けるはずもない。

と、説明すると「そもそもミクロとマクロの境界はどこにあるのか」という疑問が生じるかもしれない。 たしかに、次のように考えるとミクロとマクロの境界問題は非常に厄介である。

しかし、次の図のようにミクロとマクロは明確に区別できないと想定すると、この境界問題はあっさり解決する。

量子力学的性質がほとんど無視できる大きさの領域においては結果は確定していると見做して差し支えない。 尚、量子デコヒーレンス等でも同様の説明は可能である。