量子力学

• 主流学説と通俗説の違い
• 主な年表
• 歴史的経緯
  • 行列力学の成立まで
  • 波動力学の成立まで
  • 標準理論へ
    • 解釈
    • 波と粒子の実在性について
    • 観測者の意識
  • 隠れた変数理論について
• 参考文献

主流学説と通俗説の違い 

相対性理論においては、主流学説＝通俗説と勘違いした人は、ほぼ全員、その通俗説を批判する。 しかし、量子力学では、不思議なことに、主流学説＝通俗説と勘違いして、かつ、通俗説を信じる人が少なくない。 この違いが生じる理由は良く分からないが、どちらも、主流学説＝通俗説とする勘違いを無批判に受け入れている。

確かに、実験では従来理論で到底説明のつかない結果が得られている。 しかし、量子力学の標準理論は、その実験結果に辻褄が合うように構築しているだけであって、実験結果を説明するうえで不要な仮定は置いていない。 そこを正しく理解できない人は「○○なんて突拍子もないことを量子力学は言っている」と言い出す。 実際には、突拍子もないのは実験結果の方であり、量子力学の標準理論は実験と整合させているだけであって何ら突拍子もないことを言っていない。 そこが正しく理解されたとしても、実験結果がどう突拍子もないのかが正しく理解されないことも多い。

量子力学の通俗説はかなり根深い。 専門の学生を名乗る人物でさえ、通俗説を真に受けていることが少なくない。 しかし、常識で考えて、物理学者が馬鹿げた仮説を無批判に受け入れるわけがない。 そう思える状況があったとしたら、真相は、次に２つのどちらかである。

• 実は、物理学者も否定しているのだが、何故か、通俗説では物理学者が支持したことになっている
• 一見、非常識に見えるが、それを受け入れるべき明確な根拠がある

疑問に思ったら、先ず、物理学者がどんな根拠に基づいてそう主張しているのかを調べてみるべきだろう。 ちゃんとした根拠が示されないなら、その情報を真に受けるべきではない。 そのような根拠のない情報は、実は、物理学者自身の言葉ではないことが多い。 「○○さんが、こう言っていた」という話が捏造されているのである。

そこで、このサイトでは、次のような原則に従って集めた情報を掲載している。

• なるべく信頼できそうな物理学者の発信する情報を掻き集める
• 歴史的経緯についても調べてみる
• 根拠のない仮説には、遠慮なくオッカムの剃刀を適用する（無根拠なら可能性を広げるのが原則）
• 前３原則に従った記述のみに留め、自ら独自仮説を提示することは絶対にしない

主な年表 

年	行列力学	波動力学	隠れた変数理論
1890	リュードベリの公式(ヨハネス・リュードベリ)
1900	プランクの法則(マックス・プランク)
1903	土星型原子模型(長岡半太郎)
1905	光量子仮説(アルベルト・アインシュタイン)	(同左)	(同左)
1911	ラザフォード散乱に基づいた原子模型(アーネスト・ラザフォード)
1913	ボーアの量子条件(ニールス・ボーア)
1916	ゾンマーフェルトの量子条件(アーノルド・ゾンマーフェルト)
????	対応原理(ニールス・ボーア)
1922	コンプトン効果	(同左)	(同左)
1924		物質波(ルイ・ド・ブロイ)
1925	量子数のない関係式(ヴェルナー・ハイゼンベルク)
1925	位置と運動量の交換関係(マックス・ボルン)
1925	ハイゼンベルクの運動方程式(ヴェルナー・ハイゼンベルク)
1925	「量子力学について」(マックス・ボルン、ヴェルナー・ハイゼンベルク、エルンスト・パスクアル・ヨルダン)
1926		シュレーディンガー方程式(エルヴィン・シュレーディンガー)
1926		「ハイゼンベルグ-ボルン-ヨルダン-の量子力学と私の力学との関係について」(エルヴィン・シュレーディンガー)
1926		「衝突過程の量子力学」(マックス・ボルン)
1927	「量子論的運動学および力学の直観的内容について」(ヴェルナー・ハイゼンベルク)
1927		確率解釈(マックス・ボルン)
1927			二重解の理論(ルイ・ド・ブロイ)
1927		電子線の回折実験(クリントン・デイヴィソンほか)
1932	「量子力学の数学的基礎」(ジョン・フォン・ノイマン)	(同左)	(同左)
1952			量子ポテンシャル理論(デヴィッド・ボーム)
1964			ベルの不等式(ジョン・スチュワート・ベル)
1967			「ブラウン運動の動力学理論」(エドワード・ウィリアム・ネルソン)
1967			コッヘン・シュペッカーの定理
1982			CHSH不等式の破れ(アラン・アスペ)

歴史的経緯 

歴史的経緯を確認すると、量子力学の標準理論は、測定時の可観測量を求めるための数式でしかなく、そこに至る過程における世界がどうなっているかの一切を記述していないことが分かる。 もちろん、標準理論と数学的に矛盾しない過程における世界を考察した理論を構築できる可能性は否定できない。 しかし、量子力学の標準理論では、過程の記述を意図的に放棄しており、測定時の可観測量の確率的期待値を求めるためだけのツールとしての数式を提示しているに過ぎない。 過程における世界を標準理論は一切を語らないのである。

標準理論は過程の一切を語っていないにも関わらず、過程を標準理論として説明する人がいるから、事態はややこしくなる。 当然のことながら、標準理論と矛盾しない過程の理論を打ち立てることは可能である。 しかし、過程の理論を打ち立てた時点で、それは標準理論ではなくなる。 次の３つをごっちゃにすると混乱の元である。

• 標準理論
• 標準理論には含まれないが、標準理論と矛盾しない理論
• 標準理論と矛盾する理論

これらを混同すると、標準理論と矛盾することを標準理論として語ったり、標準理論にない制限を標準理論の制限として語ったりすることになる。 それは量子力学の珍妙な通俗説の第一歩となる。 ネット等で一般人が言及する過程の理論のほとんどが、標準理論と致命的に矛盾するか、標準理論にない制限を標準理論の制限として扱っている。 Dr.Quantumによる二重スリット実験トンデモ解説などは、標準理論と致命的に矛盾する通俗説の最たるものだろう。

行列力学の成立まで 

初期の量子力学の課題は原子内部での電子の振る舞いをどう記述するかである。 行列力学は、一言で言うなら、壊れない安定した原子モデルのための理論である。 そして、それは、ラザフォード散乱や原子の発光および吸収スペクトル等の原子に関する実験結果と整合するように作られている。 しかし、一方で、マスクウェルの方程式の元になる電磁気学の実験結果等とは必ずしも整合を取ろうとしていない。

アーネスト・ラザフォードは、ラザフォード散乱により、原子核の存在を確認し、その周囲に電子が存在することを証明した。 しかし、マクスウェルの方程式によると、プラスの電荷の周りをマイナスの電荷が回転する場合は、電磁波が放出して、電子の運動エネルギーが失われて一瞬で原子が崩壊してしまう。 それに対して、ニールス・ボーアは、リュードベリの公式で示されるように水素の真空放電のスペクトルが飛び飛びになる事実を元に、電子の軌道は量子条件を満たす軌道に限られ、その場合は電磁波を放出しないという仮説を発表した。 しかし、ニールス・ボーアは、そうなる理由を全く説明していない。

ボーアやゾンマーフェルトの議論は、原子物理学的な現象の背後に何らかの法則が存在することを示唆するが、その内容は、ニュートン力学を部分的に利用したつぎはぎだらけのもので、一貫性がない。 そこで、ボルンやハイゼンベルグらがまず行なったのは、そうした議論から、一貫性を損なう要因を取り除くことだった。 「電子は安定した楕円軌道を描いて運動するが、時折、別の楕円軌道にジャンプする」と言ってみたところで、それが、何を意味するか全く理解できない。 そもそも、原子の内部で電子がどのように運動しているかを観測によって確かめることは技術的に困難である。 理論の体系化を阻害する元凶は、安定した軌道運動の突然のジャンプという異質な概念が混在していることのように思える。 ならば、「軌道を描いて運動する」という考え方そのものを排してしまおうというのが、行列力学の出発点となる。

「量子論はなぜわかりにくいか」(ISBN-10:4774188182,ISBN-13:978-4774188188,著:吉田伸夫)P.60

ボーアやゾンマーフェルトの量子条件を適用すると、原子がエネルギーを受け取ったり放出したりした時に「安定した軌道運動の突然のジャンプ」が必要となる。 行列力学では、そのことに対する理論的説明を試みるのではなく、「軌道を描いて運動する」という考え方を放棄することで解決を図っている。 尚、行列力学でも可観測量(位置、運動量との物理量)を考慮するが、その意味は次のとおりである。

ならば、軌道という概念を排し、実験・観測で裏付けられる量だけを扱う行列力学では、q_nnは、状態nにある電子の位置を繰り返し測定した時の平均値、あるいは、統計的な期待値と見なすべきだろう。

「量子論はなぜわかりにくいか」(ISBN-10:4774188182,ISBN-13:978-4774188188,著:吉田伸夫)P.62

ボルンやハイゼンベルグら、次のようなことを元にして可観測量を求める理論の体系化を試みた。

• 対応原理（量子数が極めて大きい極限では量子力学と古典力学の計算は一致する）
• 原子の安定状態ではエネルギー量は変化しない
• リュードベリの公式を満たす量子条件(ゾンマーフェルトの量子条件)

その結果、位置と運動量の交換関係と呼ばれる式が求められ、それを元にハイゼンベルクの運動方程式が求められた。 ハイゼンベルクの運動方程式を元に、ボルン、ハイゼンベルグ、ヨルダンによって行列力学が確立する。

そうして最終的に，1925年の11月，ボルン-ハイゼンベルグ-ヨルダンの連名による“量子力学について”(Zur Quantenmechanik Ⅱ)なる論文が完成されることになる。 この論文では，今日行列力学として知られる全内容が提示され，ユニタリー変換による物理量の対角化，さらに摂動論にまでわたっている。

「シュレーディンガー選集1波動力学論文集」(ISBN-10:4320031245,ISBN-13:978-4320031241,著:田中正・南政次,監修:湯川秀樹)P.2

結果、行列を用いた計算で可観測量が確率的に求められるようになった。 尚、波動性と粒子性の二重性と良く言われるが、行列力学では量子の波動性は一切考慮していない。 粒子性についても、測定時の可観測量は考慮しているが、その軌道等の過程を意図的に理論から外しており、粒子性の完全な記述は行なっていない。 このように行列力学は、原子内の電子の状態遷移を定式化するために考案されたものであって、量子の波動性や粒子性を記述するために考案されたわけではない。 その際、電子や光子のエネルギー最小単位については考慮されているが、意図的に粒子的な振る舞いを記述から外しているので、これらを粒子として扱っているとは言い難い。 当然、波動性については全く考慮していない。

先にこの歴史的事実に言及せず、真っ先に波動性と粒子性の二重性を説明することは、量子力学の理解の致命的な妨げとなろう。 行列力学を一般人にも分かりやすいように説明することは困難である。 しかし、如何にして標準理論が過程への言及をバッサリ切り捨てたのか、その経緯を理解してもらうためには、その歴史的事実を説明する必要がある。

波動力学の成立まで 

アインシュタインは、光電効果の実験結果を元に、光がエネルギーの最小単位を持つとする光量子仮説を発表した。 さらに、アーサー・コンプトンは、光が粒子的振る舞いをするコンプトン効果を発見した。 ルイ・ド・ブロイは、波と考えられていたものに粒子性が認められるなら、これまで粒子と考えられていたものにも波動性があるのではないかと考えた。 電子を波と考えると、ボーアやゾンマーフェルトの量子条件は原子核の周りに電子の波の定常波ができるケースとして説明できる。 そして、λ＝h/mvと仮定すると、定常波ができるケースはボーアの量子条件と数式が完全に一致した。 アインシュタインの論文を通じてルイ・ド・ブロイの物質波の概念を知ったシュレーディンガーは、その波の振る舞いをシュレーディンガー方程式として定式化し、波動力学を提唱した。 そして、シュレーディンガーは、論文「ハイゼンベルグ-ボルン-ヨルダン-の量子力学と私の力学との関係について」において、行列力学と波動力学が数学的に等価であることを証明した。 その後、クリントン・デイヴィソンらは電子線の回折実験で電子に波動性があることを実証した。

波動力学は、行列力学のような特殊な制約等にしばられず、古典力学の範囲で量子力学を記述しようとしたものである。 そして、量子の波動性に関する限りでは、古典力学の枠内での記述に成功している。 行列力学の確立に関わったボルンも、論文「衝突過程の量子力学」の中で非周期系(ようするに、原子核の周り以外)で波動力学の優位性を認めている。 さらに、波動力学は、行列力学と比べて、物理的にどのような現象が起きているのかわかりやすい。

波動力学の論文が発表された時点で、既に、霧箱の中の電子は線状の痕跡を残すことが知られていた。 これは、電子が、粒子状の性質を維持したまま、霧箱の中を移動していることを示す。 シュレーディンガーは、波が物質の実態であるという波動一元論の立場をとり、霧箱の中の電子のような粒子として観測されるものは一点に凝集した波だとして、凝集した状態を持続的に維持可能であると予想していた。 しかし、ハイゼンベルクの論文「量子論的運動学および力学の直観的内容について」において、凝集した波は時間とともに広がってしまうことが明らかにされている。 結局、シュレーディンガーは、波が一点に凝集した状態を持続的に維持可能な波動一元論を完成することはできなかった。

ボルンは解決策として確率解釈を提唱した。

Bornによる一番初めのφ関数の確率解釈を要約すれば次のように言うことができる． すなわち，|φ|²dτは体積要素dτの内部にその粒子を見出すことの確率密度の尺度を与えるが，その際粒子は各瞬間にあるきまった位置とあるきまった運動量の両者をもっている一つの質点として古典的な意味で考えられている． つまり， Schrödingerの見解とは対照的に，φは物理系を表すものでもなければ，またその物理的属性を表わすものでもなく，もっぱら後者についてのわれわれの知識を表わすにすぎない．

---

こうした数々の成功にもかかわらず，Bornの最初の解釈は，電子の回折のような回折現象の説明に適用された場合には惨憺たる失敗に終わることが明らかになった． たとえば，２重スリットの実験では，Bornの最初の解釈の意味するところによれば，両方のスリットを開いたままでスリットの背後の記録用のスクリーン上で感光して黒くなるところは，一方のスリットだけを開いたときに別々に得られる２種類の個々の黒点の重ね合せになるはずだということになる． 実験による事実としては，両方のスリットを開いたままにした時の回折パターン中には全く黒くならない領域が存在し，しかもその同じ領域は一方のスリットだけが開いている場合には黒く濃くなっている，ということになる． この実験事実はまさしくBornの最初の言い方による確率解釈への反証になっている． しかも，この２重スリットの実験は輻射の強度を減少していって，装置全体を一時に通過する粒子(電子，光子等)が１個だけという強度の強さででも実行可能である． そうである以上，数学的な解析から，明らかにそれぞれの粒子に付随しているφ-波は自分自身と干渉しており，この数学的な干渉はスクリーン上でのそれらの粒子の物理的分布によって現実化されている，ということになる． したがって，このφ関数なるものは，もしもそれが古典的意味での粒子に関して言われるものであるとするならば，物理的に実在するあるものでなければならず，単にわれわれの知識の一つの表現に過ぎないものではないはずである． しかし，そうだとすれば先に挙げた五つの困難によってあらゆる解決への試みは打ちくだかれる.

事実、HeisenbergはBornのアイディアをすぐさま受け入れたものの，これらのφ-波がSchrödinger方程式に従って時間と共に発展しかつ空間中を伝搬していくという事実を考えれば，それらを単に一つの数学的仮構とみなすよりはむしろそれらに何らかの種類の物理的実在性を付与することが必要であると考えた． 後年になってHeisenbergの記したところによれば，当時の彼はこういった確率の波を，“Atistorelesの哲学におけるδύναμις[可能性]の概念－後のラテン語の訳語によればpotentiaの概念－の定量的定式化”として理解していたという． Heisenbergはつづけていう“それは，事象は決して専断的なやり方で決定されるのではなく，ある事象が生起する確率ないしは‘傾向’がある種の実在性をもつという考え方である． 物質という厳然たる実在性とアイディアないしはイメージという知的な実在性の中央に実在のある種の中間的な層を考えるというこの考え方は，Atistoreles哲学において決定的な役割を演じる． 現代の量子論においてこの概念は新しい形態をとる：それは定量的には確率として定式化され，数学的に表現可能な自然法則に従うのである．”

「量子力学の哲学　上」(ISBN-10:4314004029,ISBN-13:978-4314004022,著:マックスヤンマー,訳:井上健)P.54-55

ただし、「波動関数を粒子の誘導場(Führungsfeld)と解釈」しても実験結果を説明するには波に実在性が必要だとハイゼンベルクは指摘している。 二重スリット実験の真相で説明した通り、二重スリット実験では、単位量の電子や光子の波どうしが干渉を起こしている。 このことは、波が単なる存在確率を示す概念に留まらないことを示している。 言い換えると、存在確率という概念が波を作り出しているのではなく、確率規則が波を存在確率と見なす概念なのである。 ようするに、波そのものは存在確率以外の何かなのである。 ただ、波と粒子との関係を論じるときには存在確率にだけ着目しようと言ってるだけなのだ。

波動力学を一般人にも分かりやすいように説明することは容易である。 しかし、一般人向けの説明は通俗説が多く、適切な説明は非常に少ない。 とくに、波動力学の最も重要な課題である空間的な広がりについてちゃんと説明したものが少ない。 空間的な広がりを持つ波と広がりのない粒子の違いが説明されていないことが多く、それゆえに両者の整合性をどう取るかの課題が明確にされていないことが多い。

また、波動性と粒子性の２つの性質を持つことが不可思議だと説明されることがあるが、これは古典力学の範囲で十分に説明可能なことである。 量子力学において、波動性と粒子性の２つの性質を持つことは古典力学の範囲で十分に説明可能だが、全ての実験結果と整合させようとすると古典力学の枠内に収まらなくなる。 古典力学で扱われる現象は、充足理由の法則(一般に因果律と呼ばれるもの)に従い、かつ、局所的な現象である。 しかし、量子力学では充足理由の法則と局所性を両立させることができない。 そこが量子力学の最も不可思議な所である。

尚、単位量の電子や光子でも波動性が生じることは、理論的には予測されていたが、長らく証明されていなかった。 二重スリット実験の真相で説明した通り、後に、二重スリット実験にて最小単位の電子や光子でも波としての性質があることが実証された。

標準理論へ 

行列力学と波動力学は、ディラックやヨルダンによって１つの理論に統合される。

1925年になって解決がもたらされた． Heisenbergのあたえた手がかりはBorn, Heisenberg, Jordanによって，そしてすぐそれに続いてDiracによって，量子論の新しい体系を造りあげられることができた． それは物理学のものとなった最初の完結した量子論の体系である． それよりも少し遅れてSchrödingerは全く異なった出発点から波動力学を見出した． それは同じ結果をあたえたし，まもなく，Heisenberg, Born, JordanおよびDiracの体系と同等なものであることが明らかにされた． DiracとJordanはこの２つの理論を，Bornによる量子論的な自然記述の統計的解釈に基づいて，１つの理論，“変換理論”に融合することに成功した． この理論では，うえの２つの理論はたがいに補足しながら１つに結合され，物理的な問題を数学的にきわめて簡単にとりあつかうことが可能とされている．

「量子力学の数学的基礎」(ISBN-10:4622025094,ISBN-13:978-4622025092,著:J.v.ノイマン,訳:井上健・広重轍・恒藤敏彦)p.5

しかし、それは、ノイマンから見ると数学的な厳密さに欠けていた。

しかし，それはまだ数学者を満足させる程まで論理的な厳密さをもって築き上げられた体系ではなかった．

「量子力学の数学的基礎」(ISBN-10:4622025094,ISBN-13:978-4622025092,著:J.v.ノイマン,訳:井上健・広重轍・恒藤敏彦)序

---

うえにふれたDiracの方法論は，その明晰さと優美さによって今日量子力学に関する大部分の文献にまさるものであるが，決して数学的厳密さの要求をみたしていない． －－たとえ数学的厳密さの要求が理論物理学で普通に行われている程度にまで当然かつ正当にゆるめられるとしても，その事情は変わらない．

---

このような考えの進め方はDiracとJordanによって量子的事象の明快な理論に仕上げられたのであるが，ここではこれ以上立ち入らないことにする． その理論ではδ(x),δ'(x)……のような“普通でない”しろもの－－それは普通のありふれた数学の枠からはみだしている－－が決定的な役割を果たしている．

「量子力学の数学的基礎」(ISBN-10:4622025094,ISBN-13:978-4622025092,著:J.v.ノイマン,訳:井上健・広重轍・恒藤敏彦)p.2,21

ディラックのδ関数は当時の「普通のありふれた数学の枠からはみだしている」ものであった。 ただし、和訳者の注釈において、後日、超函数の理論として「普通のありふれた数学の枠」になったことが指摘されている。

尚、ノイマンはディラックのδ関数を数学的フィクションと評した（関数:Functionと創作:Fictionを掛けた駄洒落）が、それは、決して、ディラックの功績を酷評しているわけではない。 δ関数だけではなく「理論物理学で普通に行われている程度」が数学的に厳密さを欠いていることを指摘している過ぎず、ディラックの功績に対しては数学者が求めるレベルには達していないとしても「その明晰さと優美さによって今日量子力学に関する大部分の文献にまさるもの」と敬意を示している。

数学的厳密さを求めたノイマンは、自ら、新たな手法で行列力学と波動力学の統一理論を構築した。

それで，２つの理論を統一する他の方法（Schrödingerの）へ移ることにする．

「量子力学の数学的基礎」(ISBN-10:4622025094,ISBN-13:978-4622025092,著:J.v.ノイマン,訳:井上健・広重轍・恒藤敏彦)p.21

---

このような不満足な状態を是正するために，Neumannはそれまで物理学者には縁の遠かったHilbert空間の理論を基礎におくことによって，論理的に一貫し，数学者にも受け入れられる形に量子力学を再構築することに成功した．

「量子力学の数学的基礎」(ISBN-10:4622025094,ISBN-13:978-4622025092,著:J.v.ノイマン,訳:井上健・広重轍・恒藤敏彦)序

---

つまり，John von Neumannによって，量子力学はHilbert空間におけるHermite作用素の算法として定式化されうること，ならびにHeisenbergとSchrödingerの両理論はこの算法の特定の表示にすぎないこと，が証明された。

「量子力学の哲学　上」(ISBN-10:4314004029,ISBN-13:978-4314004022,著:マックスヤンマー,訳:井上健)P.33-34

ノイマンは射影仮説(いわゆる波動関数の収縮)を導入し、後述するNO-GO定理により自然が“充足理由の法則”(一般に因果律と呼ばれるもの)を「超越する」としている。

そのようなふるまいの根拠としてとにかく２つのことが考えられる；

Ⅰ．我々の集団に属する個々の系S₁,……,S_Nは種々の状態にあることができ，集団［S₁,……,S_N］はその相対的な頻度によって定義される． この場合に物理量に対して鋭い値がえられないのは，われわれの無知のためである； 実際，どの状態に対して測定をしたかを知らないのであり，したがってどの値がえられるかをいうことはできない．

Ⅱ．個々の系S₁,……,S_Nはすべて同じ状態にあるが，しかし自然法則が因果的でない． そのときは，われわれの無知が分散の原因なのではなく，“充足理由の法則”を超越する自然そのものが原因である．

Ⅰ．の場合は一般に知られているが，重要でありかつ新しいのはⅡ．の場合である． そのような場合が存在することについて人々がはじめ懐疑的になるのは確かであろうが，しかし，この場合が現れるか現れないかの判断を可能にする客観的な基準をわれわれは見出すであろう． はじめ，そのような場合が考えられること，および，それが意味をもつことに対して，きびしい反論がなされうるようにみえる． しかしわれわれは，そのような反論は成り立たず，いくつかの困難（たとえば量子力学における）からの唯一のぬけ道はⅡ．であると信ずるのである．

「量子力学の数学的基礎」(ISBN-10:4622025094,ISBN-13:978-4622025092,著:J.v.ノイマン,訳:井上健・広重轍・恒藤敏彦)p.240,241

このノイマンの数学的手法が今日の標準理論の原型として採用されている。

解釈 

射影仮説は、間接的に推測される波動性と測定結果の粒子性を計算上で無理やり辻褄を合わせたものと見ることもできる。 射影仮説を用いた計算では、計算結果が実験結果と尽く一致する。 しかし、計算上の辻褄は合っているが、射影仮説が実際の現象を表しているかと言えば、必ずしも、そうとは言い切れない。 標準理論においては、過程について言及しない行列力学の作法が維持されており、結果を確率的に求めることしかできない。

もっと極端に言えば、量子力学の標準理論は過程の現象である波動性も粒子性も考慮していないのである。 …と言うと少々言い過ぎかもしれないが、標準理論は、数学的な計算手法を提供しているだけであって、その物理的意味まで記述していない。 波動性に見える数式は、計算方法として用意しているだけであって、それが現象としての波動性を示しているかどうかについて標準理論は一切言及しない。 また、粒子性に見える結果についても、計算結果として示しているだけであって、それが粒子性によってもたらされた性質であるかどうかについて標準理論は一切言及しない。 ただ、現実には、波動性や粒子性と解釈できる現象が推測され、それは標準理論の数学的枠組みとも矛盾しないため、量子力学では波動性や粒子性について言及される。 しかし、波動性や粒子性は標準理論の概念には含まれていないので、波動性や粒子性に言及した時点で標準理論とは呼べなくなる。 もちろん、標準理論は量子の波動性や粒子性を否定しているわけでもない。 しかし、波動性や粒子性に言及すると、それは標準理論の外側に一歩踏み出した話となる。

ようするに標準理論の言っていることは「数学的にはこうなりますが現実の現象がどうなっているかは知ったこっちゃありません」である。 そして、過程の現象について実証された理論も現存せず、また、過程の現象を実証することも原理的に不可能である。 標準理論に関して可能性のある解釈として過程の現象に言及することが関の山であるため、過程の現象に言及したものは量子力学の解釈と呼ばれる。

波と粒子の実在性について 

次のように主張する者もいる。

• 波動関数は確率の波であって実在しない
• 多数の粒子の可能性が重なり合って実在している

しかし、それは標準理論ではなく、そうしたことへの言及は量子力学の解釈の問題となる。 標準理論での扱いは次のとおりである。

• 波動関数は確率を表すが、その実在については明示しない
• 可観測量は測定時に決定するが、過程の粒子性については明示しない

では、標準理論から一歩進んで、個々の解釈として、それぞれの実在を論じるとどうか。 まず、波動性については、先に説明したとおり、「波動関数を粒子の誘導場(Führungsfeld)と解釈」することは波の実在性を否定することにはならない。

粒子については、数式上では、多数の粒子の可能性が重なり合った状態を記述している。 しかし、標準理論は、あくまで計算上での辻褄を合わせているだけであって、その実在についてまでは示していない。 そして、それが実在を記述しているのかどうかは諸説あろう。 二重解の理論のように、標準理論と数学的に等価な理論において単一の粒子の実在を想定する理論もある。

観測者の意識 

ノイマンが意識解釈を提唱したと主張する者がいる。 意識解釈は、主観的な知覚が結果を決めるとする解釈である。

物理学講師の吉田伸夫氏は、ノイマンが自著にて「人間のような意識を持った観測者」が測定すると波動関数が収縮することに言及しているとしながらも、 実は、ノイマンは、あくまで数学的に状態変化の式を記しているだけ シュレディンガーの猫 - 科学と技術の諸相 として、ノイマンが積極的に意識解釈を主張したとする考えを否定している。 「量子力学の解釈問題―実験が示唆する『多世界』の実在」の著者であるColin Bruce氏も、ノイマンが積極的に意識解釈を主張したとすることには、その著作の中で懐疑的な見解を示している。

ノイマンが「量子力学の数学的基礎」第６章で述べていることは非常にわかりにくいが、良く読めば意識解釈を肯定していないこと分かるだろう。 第６章の内容を簡単に箇条書きする次のようになる。

• 観測と主観的な知覚は結びついている
• 物心並行論は科学の基本的な要請である
• 物心並行論では、測定する側とされる側の境界は任意の場所に設定できる
• ノイマンが提唱した数学的手法では境界を任意の場所に設定できるから物心並行論を満足している

第１に，観測すること，あるいは，それに結びついた主観的な知覚の過程は，物理的環境にとって新しいなにか（Wesenheit）であって，これに帰着させることができないということは，それ自体としては全く正しい．

---

しかし，われわれの問題にするのが水銀の器までか，温度計の目盛りまでか，網膜までか，あるいは脳までか，ということにかかわりなくいちどは，これこれが観測者によって知覚されたといわなければならないのである．

「量子力学の数学的基礎」(ISBN-10:4622025094,ISBN-13:978-4622025092,著:J.v.ノイマン,訳:井上健・広重轍・恒藤敏彦)P.333-334

確かに、ノイマンは測定と主観的な知覚の関係について言及しており、両者が切り離せないことを指摘したものと見て良いだろう。 しかし、これだけでは、ノイマンが意識解釈を提唱したことにはならない。 ノイマンの主張を知りたければ、その後の記述がどのように書かれているかを読まなければならない。

第１に，観測すること，あるいは，それに結びついた主観的な知覚の過程は，物理的環境にとって新しいなにか（Wesenheit）であって，これに帰着させることができないということは，それ自体としては全く正しい． というのは，主観的な知覚はわれわれを制御のきかない(どんな制御の試みもすでにそれを前提としているから)個人の精神的な内的生活へと導くからである(さきの議論を参照)． しかしながらつぎのいわゆる物心平行論（Prinzip vom psycho-physikalishen Parallelismus）は科学的世界観にとって基本的な要請である． すなわち，実際は物理外の過程である主観的な知覚過程を，あたかもそれが物理的世界において生じたかのように記述すること，すなわち，その過程の部分を客観的な環境の中の，通常の空間内における物理的過程に対応させることが可能でなければならないということである

「量子力学の数学的基礎」(ISBN-10:4622025094,ISBN-13:978-4622025092,著:J.v.ノイマン,訳:井上健・広重轍・恒藤敏彦)P.333

ここで、ノイマンが「物理的環境」「に帰着させることができない」「制御のきかない個人の精神的な内的生活へと導く」「主観的な知覚」と対比させて「科学的世界観にとって基本的な要請」である物心並行論の必要性を論じていることに注目してもらいたい。

さて、ノイマンは、100年に1人と言われる偉大な数学者として知られており、その論理的思考力も極めて高いであろうから、自身が科学者ではないことを十分に弁えているだろう。 であれば、ここで、「科学的世界観にとって基本的な要請」でないものを「科学的世界観にとって基本的な要請」と断言するとは考えにくい。 もちろん、「科学的世界観にとって基本的な要請」となる理由を論理的に丁寧に説明したうえであれば、新たな定義を持ち出す可能性はないとは言えない。 しかし、ノイマンは、ここではそうした説明を一切していない。 これでは、自身が科学者ではないことを弁えていない限り、新たな定義を持ち出したと考えることは難しい。 とすれば、「科学的世界観にとって基本的な要請」は、ノイマンが独自に定義した考えではなく、既に、科学者の間で共通認識とされている考えを引用した(つもりだ)と考えるべきだろう。 また、科学者ではないからといって、論理的思考力も極めて高いであろうノイマンが、「科学的世界観にとって基本的な要請」を180°真逆に取り違えるとは考えられない。 よって、ここでは、以上を踏まえて物心並行論とは何かを考える。

一般に、物心並行論とは、物理現象と精神は並行しており、精神が物理現象に影響を与えないとするものである。 つまり、これは、意識解釈とは真逆である。 ノイマンは、物心並行論を満足するには「物理外の過程である主観的な知覚過程を，あたかもそれが物理的世界において生じたかのように記述する」必要があることに言及している。 つまり、これは、「物理外の過程である主観的な知覚過程を，あたかもそれが物理的世界において生じたかのように記述」できなければ、物心並行論に反してしまう、すなわち、精神が物理現象に影響を与えてしまうと言っているのである。 すなわち、「主観的な知覚過程」を他の物理現象とは全く違う別の現象と捉えると、意識解釈が必須になり物心並行論に反すると指摘しているのである。 以上の結果、結論として、物心並行論の原理の内容は次のようになると説明されている。

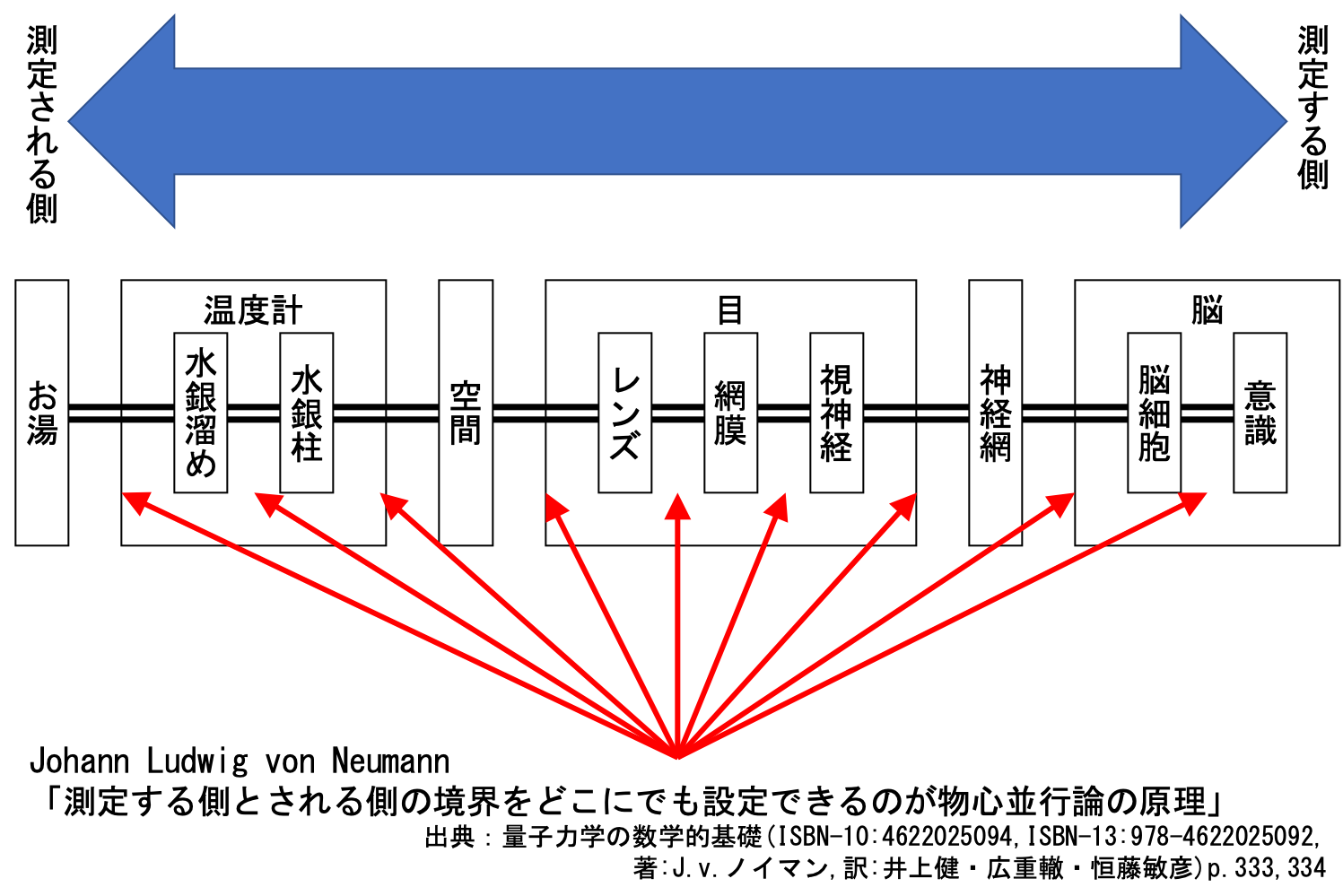
この説明はわかりにくく、測定する側とされる側の境界をどこにでも設定できることが物心並行論の原理だと主張している理由は説明文からは読み取り難い。 しかし、常識で考えれば、意識解釈を前提とした場合、観察者の意識だけが特別な存在であり、測定する側とされる側の境界は意識とそれが認識する対象の間に固定されるはずであろう。 逆に、観察者の意識も他の物理現象と対等であるならば、当然、図の全ての箇所は対等となるはずである。 ノイマンの言う物心並行論が後者を指すものであることが明らかであるから、ノイマンは物心並行論が意識解釈を前提としないものであることを説明しているものと考えられる。

以上の通り、確かに、ノイマンは、一連の現象から意識を持った観測者の「主観的な知覚過程」が切り離せないことには言及している。 しかし、一方で、「主観的な知覚過程」を特別視すると、理論が意識解釈に依存とすることになり、「科学的世界観にとって基本的な要請」に適合しなくなることにも言及している。 ただし、ノイマンには、意識解釈を積極的に否定する意図があったかどうかは不明である。 しかし、持論に意識解釈が必須ではないこと、すなわち、持論が意識解釈に依存しないことを積極的に示しそうとしたことは疑う余地がない。 平たく言えば、ノイマンの主張は「意識が物理現象に影響を及ぼすとは考えにくいから、意識だけを特別扱いすべきではない、意識も物理的過程に組み込んで他の現象と対等に扱わないといけない」ということである。 よって、ノイマンが意識解釈を提唱したとする主張は歴史的に明らかに誤った主張である。

意識解釈を支持する人たちの間では、ノイマンが言及したことは可観測量が決定される箇所であり、それは限りなく意識に近い側でなければならないとノイマンが主張したことになっている。 しかし、ノイマンが「量子力学の数学的基礎」第６章で述べていることは全く違う。

• ノイマンが言及したことは、測定する側とされる側の境界であって、可観測量が決定される箇所ではない
• ノイマンは、境界はどこにでも任意に設定できるとしており、限りなく意識に近い側でなければならないとは言っていない

ノイマンのこの説明は、量子測定理論ではさらにHeisenberg cutという考えに拡張される。 任意に設定できる境界のうち、測定する側が測定される側に与える影響が無視できる程度に小さい箇所をHeisenberg cutという。 この場合、可観測量はHeisenberg cutよりも測定される側で決定されていると考えて差し支えない。 つまり、このノイマンの説明は、可観測量が決定される箇所を意識に近づけているのではなく、むしろ、意識から遠ざけているのである。

隠れた変数理論について 

アインシュタインらは、標準理論では結果を確率的にしか予測できないが、物理現象としては常に確定した値をもっているとした隠れた変数理論を提唱した。 一方で、ノイマンは、書籍「量子力学の数学的基礎」で、標準理論に適合する隠れた変数理論が成立しないことを証明した(不可能性を示す定理をNO-GO定理と言う)。 ノイマンのNO-GO定理には様々な批判があり、しばらくは決着がつかないままであったが、今日では、ノイマンはNO-GO定理が全ての隠れた変数理論を否定するわけではないことがわかっている。 また、隠れた変数理論の否定とノイマンの言う「物心並行論の原理」を併せるとシュレーディンガーの猫のような問題を引き起こすと考えられていたが、今日では、量子測定理論の知見によりHeisenberg cutを設定することによりこのような問題が生じないことが分かっている。 いずれにせよ、ノイマンは、隠れた変数理論を否定的に証明した（と本人は思っている）のだから、射影仮説を採用するのは極めて自然な判断だろう。 というのも、隠れた変数理論が否定されるなら、射影仮説なしで理論と実験結果の辻褄を合わせることは非常に困難だからである。 だから、実験結果と辻褄の合う理論に限れば、次の２つ以外の理論はほぼ見かけない。

• 射影仮説と等価な何かを仮定する
• 隠れた変数理論

多世界解釈においても、知覚可能な世界のみを抽出した結果は射影仮説と等価となる。 多世界解釈から多世界を差し引いたものはconsistent historiesと呼ばれ、射影仮説がデコヒーレンスに置き換わっただけに過ぎない。 隠れた変数理論には、二重解の理論とその派生理論以外にも、アインシュタインが支持した統計解釈や時間対照的な解釈などがあるようである。 多世界解釈も、原理から確率を外そうとした点では隠れた変数理論の一種とみなせる。 いずれにせよ、実験結果と辻褄の合うものに限れば、前者でも後者でもないものは皆無である。 前者か後者であれば、二重スリット実験もきちんと説明できる。

有名なEPR論文の触発されたジョン・スチュワート・ベルは、充足理由の法則(一般に因果律と呼ばれるもの)に従う２つの現象の相関確率の限界を示すベルの不等式を提唱した。 局所的隠れた変数理論は２つの現象の測定結果に相互作用が働かない限りベルの不等式を満たすが、量子力学の標準理論は相互作用の有無に関わらずベルの不等式を破る。 もしも、局所的な相互作用が働き得ない実験でベルの不等式を破らないのであれば、量子力学の標準理論は相互作用が働かない限りベルの不等式を満たすように修正する必要があった。 後日、アラン・アスペらの実験により、局所的な相互作用が働き得ない実験の結果がベルの不等式を破ることが判明した。 この結果、局所的隠れた変数理論が否定されることになった。 ただし、ベルの不等式の破れが意味することは、充足理由の法則の破れなのか、局所性の破れなのかは定かではない。 というのも、局所的な相互作用が働き得ない条件であっても、非局所的な相互作用が働いている可能性は否定できないからである。 相互作用が働いていれば充足理由の法則を満たしていてもベルの不等式は破れ得る。 もしも、非局所的な相互作用が働いているとすれば、それは局所性の破れを意味する。 だから、この実験結果は、充足理由の法則か局所性のいずれかが破れていることを示している。 よって、充足理由の法則が破れている標準理論も、局所性を満たさない非局所的隠れた変数理論も、いずれも、ベルの不等式の破れと矛盾しない。 ちなみに、ベルの不等式は量子もつれの相関性を利用して検証しているが、充足理由の法則が破れるなら量子もつれに相関性が生じる仕組みの説明が困難となる。 量子もつれに相関性がなければ、ベルの不等式の検証は不可能であり、そもそも、量子もつれとして特別視されることもなかった。 よって、アラン・アスペらの実験は、充足理由の法則の破れではなく局所性の破れを実証したと解釈した方が自然であろう。

尚、井元信之氏は、 決定論的量子力学? ボーム理論はどこまで行くか?(大阪大学基礎工学研究科 井元信之) - 高知工科大学 にて、局所性の制限はブラックボックスの外からのaccessible(アクセス可能)な現象のみに適用されるのであって、ブラックボックスの外からのaccessible(アクセス可能)でない所で非局所性が現れても相対性理論には反しないとしている。 また、この実験についてベルの不等式を破ることが完全に証明されたとは言えないとする批判もいくつか存在する。

さらに、コッヘン・シュペッカーの定理では、標準理論において全ての可観測量に決まった値を割り振ることはできないとされている。 しかし、この定理を回避した隠れた変数理論も可能であるとされている。

最初の頃は、隠れた変数理論は、標準理論よりも遥かに妥当な理論であったのだろう。 この頃、多くの物理学者が隠れた変数理論をまじめに研究しなかったことは非常に残念である。 アインシュタインが隠れた変数理論に固執したのは、それが定性的に最も素直な解釈だったからだろう。 しかし、今日では、当初考えられていたような素直な形での隠れた変数理論が実現不可能であることがわかっている。 隠れた変数理論が正しくない証明は困難であるが、実験等と辻褄の合う隠れた変数理論を構築しようとするとかなり歪な理論になってしまう。 隠れた変数理論を安易に否定することはできないが、執拗なまでに固執すべき理由は今日では失われたと考えて良いだろう。

まとめよう。 定性的に見れば、射影仮説は、非常に奇妙な仮説に思える。 しかし、様々な実験結果や数学的研究結果を踏まえると、隠れた変数理論もそれと同じか、あるいは、それ以上の奇妙な理論となる。 そして、実験結果と辻褄の合う理論のみに限れば、その両者以外の選択肢はありそうもない。 つまり、選択肢が複数あって、そのどちらも非常に奇妙なのである。

－コペンハーゲン解釈の「量子力学と古典力学が混在している世界」、多世界解釈の「すべてが量子力学で表される世界」、ボーム解釈の「すべてが古典力学で表される世界」。 この三つの量子の世界の解釈について、それぞれ印象を語っていただきました。 三つのうちのどれに分がある、とお考えですか。

少し言いましたように、今のところ実験結果からは、三つの解釈のどれがどれくらい正しいかということは言えません。

「SF小説がリアルになる　量子の新時代」(ISBN-10:4022732873,ISBN−13:978-4022732873,著:佐藤文隆/井元信之/尾関章)kindle版p.174-175

これは、例えるなら、カレー味のウ○コかウ○コ味のカレーかという究極の選択と変わらない。 悪い意味で２つの選択肢の優劣は付け難く、できればどちらも選ばない方が良さそうである。 しかし、選ばないという選択がないなら、どちらを選んだとしても五十歩百歩である。 以上を踏まえれば、射影仮説を計算上のツールとして扱って現実に起きていることを棚上げするコペンハーゲン解釈が最も理性的な判断に見える。

参考文献 

• 「量子論はなぜわかりにくいか」(ISBN-10:4774188182,ISBN-13:978-4774188188,著:吉田伸夫)
• 「量子という謎」(ISBN-10:4326700750,ISBN-13:978-4326700752,著:白井仁人・東克明・森田邦久・渡部鉄兵)
• 「量子力学の哲学　上」(ISBN-10:4314004029,ISBN-13:978-4314004022,著:マックスヤンマー,訳:井上健)
• 「量子力学の哲学　下」(ISBN-10:4314004274,ISBN-13:978-4314004275,著:マックスヤンマー,訳:井上健)
• 「シュレーディンガー選集1波動力学論文集」(ISBN-10:4320031245,ISBN-13:978-4320031241,著:田中正・南政次 ,監修:湯川秀樹)
• 「量子力学の数学的基礎」(ISBN-10:4622025094,ISBN-13:978-4622025092,著:J.v.ノイマン,訳:井上健・広重轍・恒藤敏彦)
• 「新版量子論の基礎」(ISBN-10:4781910629,ISBN-13:978-4781910628,著:清水明)