波動関数トンデモ解説
はじめに
本ページは波動関数の一部である。
実例
「箱の中の古典的なサイコロの目の確率」を用いた誤謬(故意なら詭弁)
サイコロを用いたトリックの概要
「系を観測をすると、その波動関数(または状態ベクトル)は収縮し、その変化はシュレディンガー方程式に従わない」と聞いて、前世紀の「観測問題」に目覚めてしまって、「波動関数とは?収縮とは?」と懊悩してしまっている物理学徒は、まず箱の中の古典的なサイコロの目の確率を考察してみて下さい。
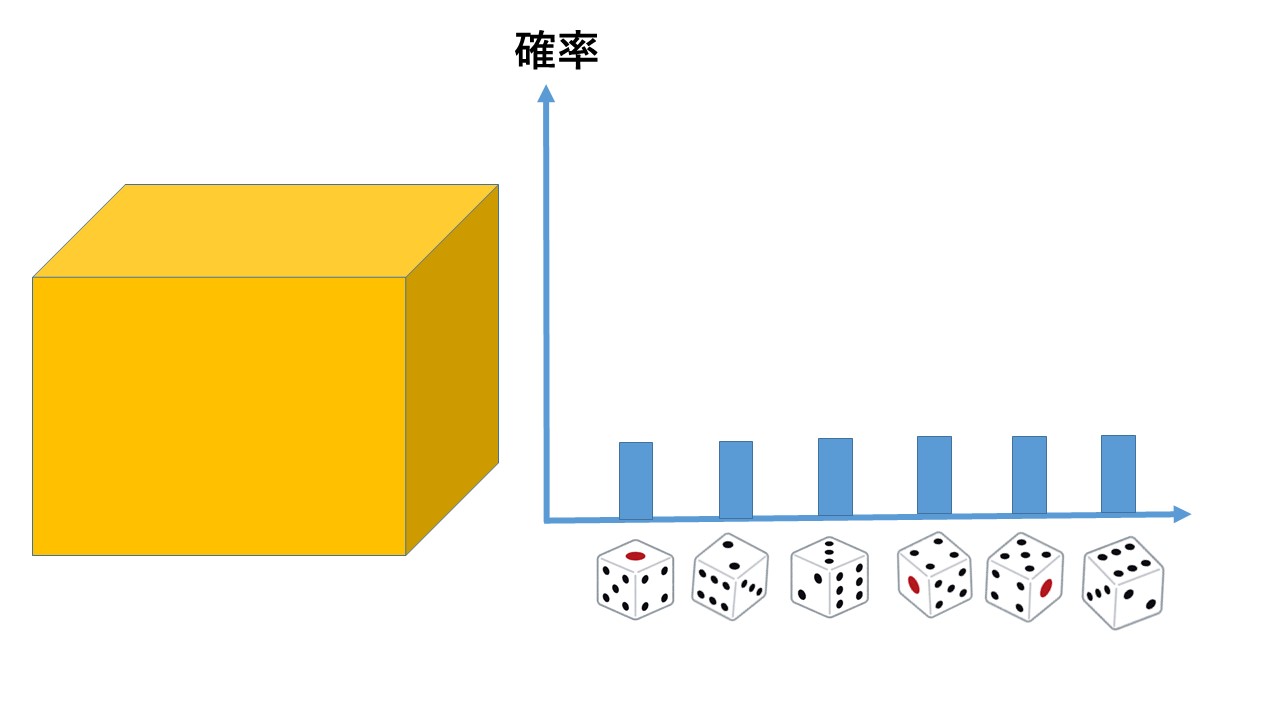
収縮の結果を人間が認識するまでには次の2つの過程がある。
- 古典力学の枠を超える確定過程
- 確定値を認識する過程
ここで説明が必要なことは、当然、前者の過程である。 しかし、この人の説明は前者の説明をせず、後者の方に注目を集めることで、前者を闇に葬り去っている。 自ら論点整理できない人はこのトリックに簡単に騙されてしまう。 しかし、自ら論点整理できる人であれば必要な説明が完全に抜け落ちていることが容易に見抜けるはずである。
「波動関数の収縮は知識、情報の増加でしかない」の誤り
知識、情報の増加でしかない「収縮」はシュレディンガー方程式を満たすわけがないのです。
2020年10月19日午前9:53(Masahiro Hotta) - twitter
これは量子であろうと古典(含む隠れた変数理論)であろうと同じで、確率の概念そのものに「収縮」が内在していることを説明する例です。 問題はありません。
2020年10月20日午後5:37(Masahiro Hotta) - twitter
古典的なサイコロでもそれを観測した人にとって確率分布は収縮するので意識は必要ですよね。 例えば、箱の中を見ていない人にとってはまだ確率分布の収縮は起きないので、観測者依存性は古典でもあるわけです。
2020年10月20日午後5:51(Masahiro Hotta) - twitter
一般に確率には意識の存在は不可欠で、それで収縮が起きるのですから。
「箱の中の古典的なサイコロの目の確率」では、周辺環境も含めた初期値(位置、速度、回転、弾性、形状、その他)は一意の値を持ち、それらが決まれば結果も一意に決まる。 天文学的な数の面があれば分子運動や量子力学的効果による揺らぎが多少結果に影響を及ぼすかもしれないが、サイコロ程度の6面体ではそうしたゆらぎはほぼ無視できる。 もちろん、初期値の測定には誤差があるし、計算式も完全ではないことがあるので、結果を人間が正確に予測できるとは限らない。 しかし、ラプラスの悪魔であれば結果を正確に予測可能であるから、初期値が確定した時点で結果が確定することは疑いの余地がない。 この結果は測定の影響を受けない。 例えば、サイコロの目が3となるべき所、これが測定の影響で4に変わることはあり得ない。 測定によって何ら結果が変わらないなら、測定を単なる「知識、情報の増加でしかない」として扱って差し支えない。
一方で、ノイマンは自著の中で、量子力学ではこのような測定の影響を受けない決定論が不可能だと証明している。
Bohmの測定の理論では問題の隠れた変数は観測される系の状態に依存するばかりでなく,また測定装置の状態にも依存するものと仮定された. そうした類の隠れた変数はVon Neumannによって考察されたことのないものである以上,Bohmとしては隠れた変数は量子力学と両立しないというVon Neumannの証明は使えないと主張することができた.
「量子力学の哲学 下」(ISBN-10:4314004274,ISBN-13:978-4314004275,著:マックスヤンマー,訳:井上健)P.340
この確定過程が古典力学の枠を超えることへの疑義があったからこそ、EPR論文やシュレーディンガーの猫やベルの不等式が生まれたのである。 もしも、波動関数の収縮が古典力学の枠内で説明できるなら、これらの論争は存在し得ない。 そして、検証実験の結果、この確定過程が古典力学の枠を超えることが実証された。 よって、波動関数の収縮は、明らかに古典力学の枠を超える確定過程であって、単なる「知識、情報の増加でしかない」ものではない。
以上の通り、波動関数の収縮と「箱の中の古典的なサイコロの目の確率」は、単なる「知識、情報の増加でしかない」かどうかにおいては性質が真逆である。 また、波動関数が「知識、情報」のみを表わすだけで物理的現象を一切記述していないとの考え方もHeisenbergらによって早くから否定されている。
Bornによる一番初めのφ関数の確率解釈を要約すれば次のように言うことができる. すなわち,|φ|2dτは体積要素dτの内部にその粒子を見出すことの確率密度の尺度を与えるが,その際粒子は各瞬間にあるきまった位置とあるきまった運動量の両者をもっている一つの質点として古典的な意味で考えられている. つまり, Schrödingerの見解とは対照的に,φは物理系を表すものでもなければ,またその物理的属性を表わすものでもなく,もっぱら後者についてのわれわれの知識を表わすにすぎない.
こうした数々の成功にもかかわらず,Bornの最初の解釈は,電子の回折のような回折現象の説明に適用された場合には惨憺たる失敗に終わることが明らかになった. たとえば,2重スリットの実験では,Bornの最初の解釈の意味するところによれば,両方のスリットを開いたままでスリットの背後の記録用のスクリーン上で感光して黒くなるところは,一方のスリットだけを開いたときに別々に得られる2種類の個々の黒点の重ね合せになるはずだということになる. 実験による事実としては,両方のスリットを開いたままにした時の回折パターン中には全く黒くならない領域が存在し,しかもその同じ領域は一方のスリットだけが開いている場合には黒く濃くなっている,ということになる. この実験事実はまさしくBornの最初の言い方による確率解釈への反証になっている. しかも,この2重スリットの実験は輻射の強度を減少していって,装置全体を一時に通過する粒子(電子,光子等)が1個だけという強度の強さででも実行可能である. そうである以上,数学的な解析から,明らかにそれぞれの粒子に付随しているφ-波は自分自身と干渉しており,この数学的な干渉はスクリーン上でのそれらの粒子の物理的分布によって現実化されている,ということになる. したがって,このφ関数なるものは,もしもそれが古典的意味での粒子に関して言われるものであるとするならば,物理的に実在するあるものでなければならず,単にわれわれの知識の一つの表現に過ぎないものではないはずである. しかし,そうだとすれば先に挙げた五つの困難によってあらゆる解決への試みは打ちくだかれる.
事実、HeisenbergはBornのアイディアをすぐさま受け入れたものの,これらのφ-波がSchrödinger方程式に従って時間と共に発展しかつ空間中を伝搬していくという事実を考えれば,それらを単に一つの数学的仮構とみなすよりはむしろそれらに何らかの種類の物理的実在性を付与することが必要であると考えた. 後年になってHeisenbergの記したところによれば,当時の彼はこういった確率の波を,“Atistorelesの哲学におけるδύναμις[可能性]の概念-後のラテン語の訳語によればpotentiaの概念-の定量的定式化”として理解していたという. Heisenbergはつづけていう“それは,事象は決して専断的なやり方で決定されるのではなく,ある事象が生起する確率ないしは‘傾向’がある種の実在性をもつという考え方である. 物質という厳然たる実在性とアイディアないしはイメージという知的な実在性の中央に実在のある種の中間的な層を考えるというこの考え方は,Atistoreles哲学において決定的な役割を演じる. 現代の量子論においてこの概念は新しい形態をとる:それは定量的には確率として定式化され,数学的に表現可能な自然法則に従うのである.”
「量子力学の哲学 上」(ISBN-10:4314004029,ISBN-13:978-4314004022,著:マックスヤンマー,訳:井上健)P.54-55
二重スリット実験の真相で説明した通り、二重スリット実験では、単一の粒子の持つ波どうしが干渉を起こしている。 このことは、「知識、情報」に留まらない何らかの物理現象が干渉を起こしていることを示している。 コペンハーゲン解釈は、波動関数による「知識、情報」にのみ着目して該当する物理現象の存在について言及しないだけであり、該当する物理現象の存在を否定しているわけではない。 もちろん、波動関数がその正体を正確に記述しているとは限らない。 しかし、既に説明した通り、波動関数がその正体とは全く無関係な記述ではないことも疑う余地はない。 よって、波動関数の収縮も単なる「知識、情報の増加」に止まらない、何らかの物理現象を反映した記述である。
波動関数の収縮とは射影仮説における次の(A)+(B)を指す。
射影仮説には,次の2つの役割がある:
(A)異なる測定値に対応する状態ベクトルの間の干渉をなくす
(B)干渉の無くなった2つの状態ベクトルのうちのどちらかを抜き出す
量子測定の原理とその問題点 by 東京大学大学院総合文化研究科広域科学専攻相関基礎科学系&東京大学大学院理学系研究科物理学専攻:清水明教授
値が確定済の「箱の中の古典的なサイコロの目」には明らかに(B)が欠けている。 よって、波動関数と値が確定済の「箱の中の古典的なサイコロの目」は、論点において類似性が全く認められない。 尚、「異なる測定値に対応する状態ベクトルの間の干渉」は量子の波動性を生み出すものであり、これは収縮前には必ず存在する性質である。 収縮前にある性質が収縮後に失われるのだから、これは単なる「知識、情報の増加」ではない。
百万歩ほど譲って、収縮によって物理現象に全く変化がなく、それが単なる「知識、情報の増加」だったとしよう。 だとすると、観測によって主観的認識が不定から確定に変化する様子は、波動関数も「箱の中の古典的なサイコロの目の確率」も大差ない。 つまり、「箱の中の古典的なサイコロの目の確率」によって元の話が全く分かりやすくなっていないのである。 よって、この場合は例え話を持ち出す必要は全くなく、収縮が物理現象ではない単なる「知識、情報の増加」を示していることを説明すれば事足りる。 しかるに、この人は、例え話による印象操作を利用して、単なる「知識、情報の増加」と考えられる理由の説明を有耶無耶にしてしまっている。 必要な説明をすれば「本当にそうなのか?」という疑問が当然発生するだろうが、本来すべき説明をすっ飛ばして印象操作で誤魔化しているために、本来生じ得る疑問を闇に葬っているのだ。 これは、主張内容が正しいかどうか以前の問題として、真っ当な説明が全くできていないことを示している。 やっていることは時蕎麦と変わらない。 「1、2、3、4、5、6、7、8、おっちゃん、今何時でえ?」 「へい、9つ(現代の午前0時)で!」 「10、11………」 お後がよろしいようで。
そもそも、ご本人が次のように発言している。
質問:「量子力学、何を考えてて、何を求めてんのかがわかんない」
回答:「位置も運動量も決まっている粒子のような局所的な実在は存在しないことが実験で分かったので、そういう実在が決して出てこない理論を考えてて、実験で計測できる観測値の出現確率を求めるのが、量子力学。」
ご本人が、位置も運動量のような可観測量は決まった値を持たないと認めている。 にも関わらず、測定すると決まった値が得られる。 決まった値を持たないものを測定すると、何故か、決まった値が出てくるのである。 それが波動関数の収縮(射影仮説)である。 よって、ここで説明すべきことは決まった値を持たないものを測定して決まった値が出てくる過程であって、その結果として出てきた決まった値を人間が認識する過程ではない。
尚、隠れた変数理論なら、値が確定済のサイコロの「知識、情報の増加」に例えて差し支えない。 しかし、局所的隠れた変数理論はベルの不等式の検証実験で否定されているから、やはり、古典力学の枠を超える現象であることには変わりない。 また、隠れた変数理論なら「『収縮』はシュレディンガー方程式を満たすわけがない」は全く意味不明である。 例えば、ド・ブロイの二重解の理論なら、波動関数の計算の対象は波動性だが、測定の対象は粒子性である。 計算対象と測定対象が違うから「収縮」のように見えるだけで、実際は収縮などしていないのである。 つまり、隠れた変数理論では、「シュレディンガー方程式を満たすわけがない」ような状態変化は生じていないのだから、「『収縮』はシュレディンガー方程式を満たすわけがない」なる説明が出てくる余地はない。
「箱の中の古典的なサイコロの目の確率」は例え話に偽装した全く別の何か
各目の出る確率は1/6で、一様分布でしたが、箱をとってサイコロを観測して3の目が出ていれば、確率分布は3の目にだけ集中して他の目は零になります。 これが「確率分布の収縮」であり、そして当たり前ですが、この確率変化はニュートン方程式に従いませんよね。
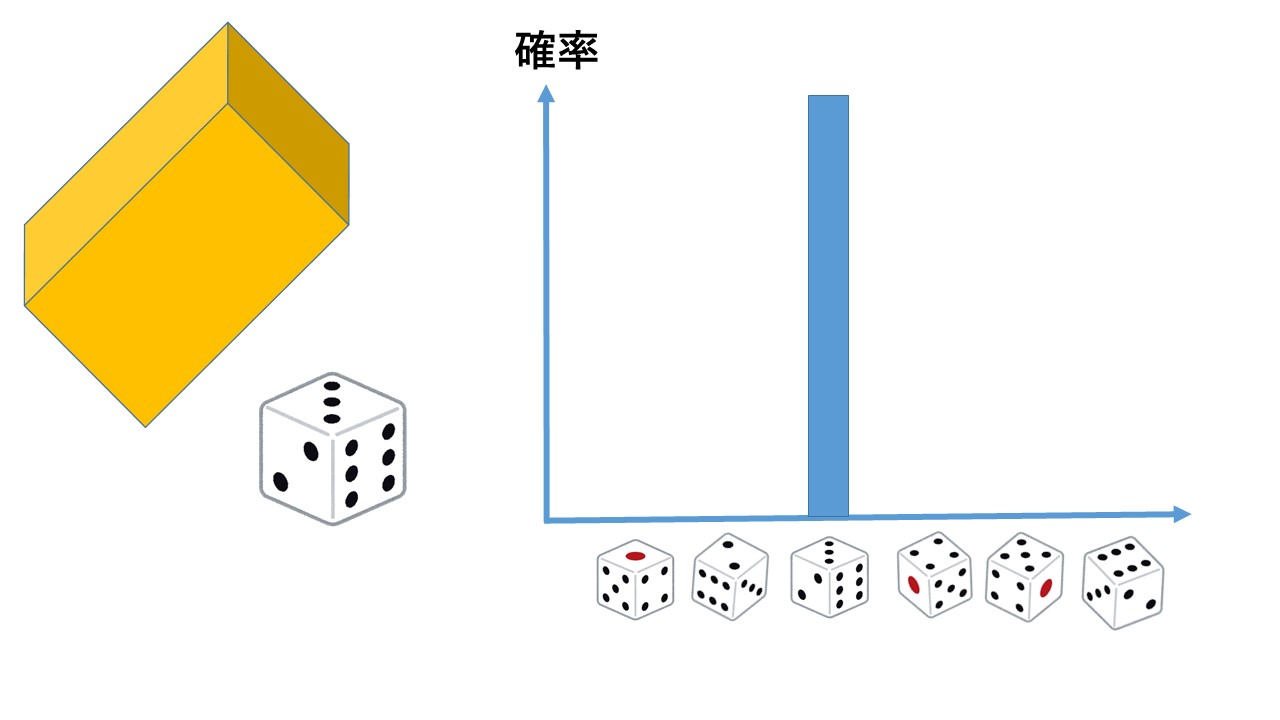
2020年10月19日午前9:49(Masahiro Hotta) - twitter
波動関数や状態ベクトルは、物理量の確率分布の集合と数学的に等価な概念に過ぎません。 ですから古典的なサイコロでも起きた「確率の収縮」が「波動関数の収縮」に対応するわけで、不思議なことでもありません。
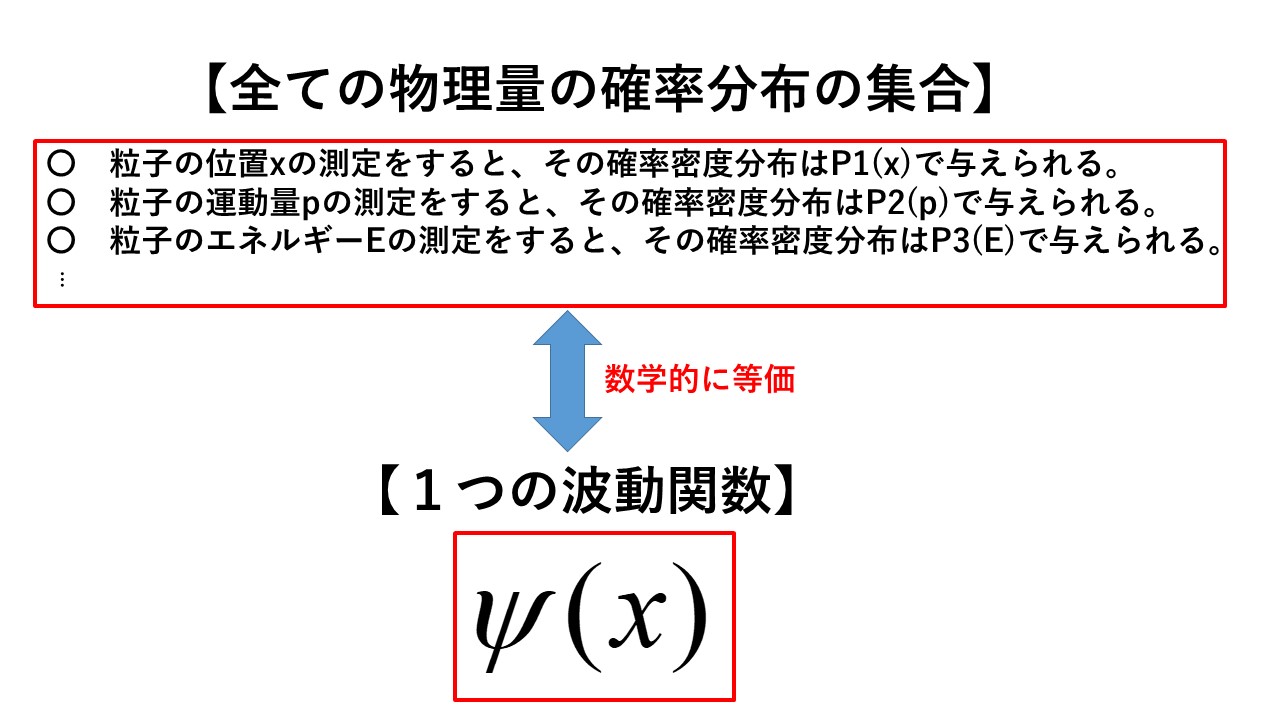
良い例え話は次の2つを満足する必要がある。
- 論点部分では良く類似している
- 論点部分以外は簡略化されている
前者を満たさない場合は例え話に偽装した全く別の何かである。 論点部分以外も同じなら例え話ではなくて、そのまんまであろう。 論点部分以外が煩雑になっていたら、元の話で説明した方がわかりやすい。
「箱の中の古典的なサイコロの目の確率」には、箱をかぶせた後の話しか書かれていないので、サイコロを振る(その後に落ちて止まる)ことが暗黙の了解に含まれているかどうか定かではない。 しかし、いずれにしても、「箱の中の古典的なサイコロの目の確率」は例え話としての必須条件を満たしていない。
- サイコロを振ることが暗黙の了解に含まれているならば、「波動関数や状態ベクトル」の収縮にはそのような明確な物理的操作が説明されていない
- サイコロを振ることが暗黙の了解に含まれていないならば、「波動関数や状態ベクトル」の収縮に相当する現象が含まれていない
前者であるならば、サイコロを振ることによって「箱の中の古典的なサイコロの目」が確定する。 一方で、波動関数の方はサイコロを振る行為に該当する物理的操作、すなわち、何が波動関数の収縮を引き起こすかが説明されていない。 今日ではその物理操作は明確になっているのだが、少なくとも当該tweetの中には一切説明がない。 それこそが物理学徒が懊悩している部分であろうから、それこそが論点である。 しかるに、当該tweetではその説明が一切為されていない。 よって、波動関数と「箱の中の古典的なサイコロの目」は、論点部分の明確さが全く違うのであり、論点において類似性が全く認められない。
後者であるならば、「箱の中の古典的なサイコロの目」は最初から確定した値を持っている。 一方で、波動関数の方は収縮前は確定した値を持っておらず、収縮後に確定した値を持つ。 よって、この場合も、波動関数と値が確定済の「箱の中の古典的なサイコロの目」は、論点において類似性が全く認められない。
宙に浮いて回転し続けていた(特殊な)サイコロが急に落下して決まった値に確定する、というような例えであれば適切な例え話となろう。 この場合、物理学徒が懊悩する内容は、当然、「何故急に例外的な落下現象が生じたか」である。 この点について一切説明せず、かつ、例え話に偽装した何かを用いて、その何かにのみ当てはまる性質があたかも元の話にも当てはまるかのような印象操作を行うなら、それは紛うことなき誤謬(故意なら詭弁)である。 これは「認識段階では既に値が確定していると仮定すれば数学的には辻褄が合う」という説明の仮定部分から目を逸らして未説明部分を闇に葬っているにすぎない。 やっていることは時蕎麦と変わらない。 「1、2、3、4、5、6、7、8、おっちゃん、今何時でえ?」 「へい、9つ(現代の午前0時)で!」 「10、11………」 お後がよろしいようで。
論点部分が全く違う「例え話」は、例え話だけが持つ性質があたかも元の話にも当てはまるかのような印象操作を与える誤謬(故意なら詭弁)である。 以上は、何も難しいことは言っていない。 論点整理すれば誰でも容易に理解できることである。
「収縮に意識の存在は不可欠」の誤り
一般に確率には意識の存在は不可欠で、それで収縮が起きるのですから。
現代科学は実験に基づいた科学である。
- 実験に合う唯一の理論は信じ難くても正しい
- 実験に合わない理論は受け入れ易くても間違い
それを否定したら量子力学は成立しない。 故に、収縮に意識が必要であるかどうかは、実験で検証しなければならない。
しかし、人間が検証した時点で人間の認識を伴う現象になるため、人間の認識を伴わない現象がどうなるのを人間が検証することはできない。 だから、人間が議論することができる現象には必ず人間の認識が伴う。 しかし、それは意識が必要な根拠とならない。 何故なら、次のいずれが正解かを検証していないからである。
- 認識がある場合には収縮が起きるが認識がない場合は収縮が起きない
- 認識があってもなくても等しく収縮が起きる
前者が正しければ収縮には意識が必要だが、後者が正しければ収縮には意識は必要である。 人間の認識を伴わない現象がどうなるのを人間が検証することはできないのだから、どちらが正しいかを検証できない。 よって、人間の意識が必要だとは結論づけられない。
収縮に人間の意識が必要ならば、シュレーディンガーの猫等で紹介したHeisenberg cutも説明が困難になる。 よって、間接的証拠から、収縮には人間の意識は不要である可能性が高い。
「観測問題」
前世紀に散々言及された「観測問題」は、現在では量子力学に存在しないことは分かっています。 波動関数は確率の束だとしっかり腹に落として、量子力学の理解を深めましょう。
確かに今日では観測問題は解決済事項である。 しかし、それは波動関数が単なる「知識、情報の増加」だからではなく、何が波動関数の収縮を引き起こすかが明らかになっているからである。 また、既に説明した通り、コペンハーゲン解釈は、波動関数による「確率の束」にのみ着目して該当する物理現象について言及しないだけであり、該当する物理現象の存在を否定しているわけではない。
「ろくに論理を詰め」ていないのは誰か
多世界解釈推しの科学哲学好きな物理屋の中には、ろくに論理を詰めず、ふわふわと多世界解釈をメタ科学化して人文系を騙す話を書く方もいるのですが、
以上説明した通り、「ろくに論理を詰め」ていないのはこの人の方である。
標準理論であるコペンハーゲン解釈に基づいた量子力学では、1つの電子の多数の異なる歴史が量子状態(波動関数)として線形的に重なります。 干渉効果はこの異なる歴史の状態ベクトルの足し合わせ係数が起こしています。 電子が波に「化けて」、水面の波のように干渉を起こしているわけではありません。
2020年11月2日午前10:25(Masahiro Hotta) - twitter
ですから、「電子は粒子なのか波なのか」という問いは、現代の量子力学としては「粒子」が正解です。 波の性質としてみなされてきた干渉効果ですが、1つの電子が辿る異なる歴史の間の干渉効果と言えます。 重ね合わさる各歴史の中では、その電子は波になんかに化けていません。
2020年11月2日午前10:28(Masahiro Hotta) - twitter
ですから、前期量子論における「電子は粒子でもあり、波でもある」と主張をする相補性の概念は、現代の量子力学の観点から言うと、とてもミスリーディングなものと言えます。
多世界解釈は、その真偽はともかく、元になったHugh Everett Ⅲの"Relative State" Formulation of Quantum Mechanics(1957)も含めて、査読付きの専門誌に掲載された論文である。 それに対して、「1つの電子が辿る異なる歴史の間の干渉効果」なる学説は、一体、何処の専門誌に掲載された論文に書いてあるのか。 多世界解釈と似たようなことを言っているように聞こえるが、そのような仮説は聞いたこともない。 根拠も示さずに独自の仮説を唐突に唱えるなら、それこそ「ろくに論理を詰めず、ふわふわと」「メタ科学化して人文系を騙す話」でしかあるまい。
驚きのHotta解釈
Hotta解釈に解説する通り、彼の解釈は次のようなものらしい。
| 物理的変化 | 標準理論 | 二重解の理論 | 多世界解釈 | Hotta解釈 |
|---|---|---|---|---|
| 干渉性の喪失 | 測定時 | 測定時 | 測定時 | 測定時 |
| 結果の確定 | 測定時 | 常時 | 測定時 | 認識時 |
この珍説のおかしさはHotta解釈にて詳細に説明する。
彼らは、波動関数は物理的実在で、その収縮も物理的過程と考えたいと思っていました。 でも現在では、波動関数は情報の束で実在ではないというのが合理的です。
2019年11月22日午前7:42(Masahiro Hotta) - twitter
21世紀の現在では、古典力学のような実在を扱う理論とは異なり、量子力学は情報理論の一種であるという認識です。 波動関数の収縮は、観測者にとっての知識の増加に伴う確率分布の変化に過ぎません。
「量子力学の哲学 上」(ISBN-10:4314004029,ISBN-13:978-4314004022,著:マックスヤンマー,訳:井上健)P.54-55によれば、「波動関数は情報の束で実在ではない」との考えはBornが確立解釈を発表した直後に否定されている。 確かに、Bornの最初の確率解釈では「φは物理系を表すものでもなければ,またその物理的属性を表わすものでもなく,もっぱら後者についてのわれわれの知識を表わすにすぎない」とされていた。 しかし、「Bornの最初の解釈は,電子の回折のような回折現象の説明に適用された場合には惨憺たる失敗に終わることが明らかになった」のである。 二重スリット実験における干渉縞は「波動関数は情報の束で実在ではない」とする考えと明らかに矛盾する。 だから、Heisenbergは「これらのφ-波がSchrödinger方程式に従って時間と共に発展しかつ空間中を伝搬していくという事実を考えれば,それらを単に一つの数学的仮構とみなすよりはむしろそれらに何らかの種類の物理的実在性を付与することが必要である」と考えたのである。 「波動関数は情報の束で実在ではない」との考えこそが100年近く前に放棄された古臭い遺物にすぎない。 21世紀の現在では、「情報理論の一種」として「観測者にとっての知識の増加」のみを計算対象とするのは、物理的実在を計算や理論の対象としないだけであって、物理的実在を否定しているわけではない。
確かに、波動関数が物理的現象そのものを記述したと考えるのは早計である。 しかし、波動関数が何らかの物理的現象と相関した関数であることには疑いの余地がなく、波動関数の背後にある何らかの物理的現象を否定することはできない。 ただ、波動関数ではその物理的現象の正体に言及できないだけなのである。
背後にある何らかの物理的現象を追求することには、多くの物理学者は否定的立場を取る。 何故なら、その労力が無駄になると予想されるからである。 だから、それを伝える目的で、波動関数が物理的現象そのものを記述していないことを「波動関数は実在ではない」と表現する物理学者はいる。 その場合は、当然、波動関数の背後にある何らかの物理的現象までは否定していない。 一方で、Hotta解釈のように、100年近く前に否定されたことを未だに主張する者もいる。
以下も参考に。
このページへのご意見は節操のないBBSにどうぞ。
総合案内
科学一般
疑似科学等
- 疑似科学
- 数学や科学への無理解
- 疑似科学を批判する疑似科学
- STAP細胞論文捏造事件
- CCS地震原因説
- 地球温暖化懐疑論
- 疑似科学者列伝