二重スリット実験(疑似科学からの脱洗脳)
最初に
量子力学の二重スリット実験について、ここでは次のようなトンデモ理論でよく採用されている説明手順と同じ手順で説明を試みる。
ただし、トンデモ理論と同様の誤りは採用しない。 同じ説明手順で科学的に正しい説明をするとどうなるかを示すのがこのページの目的である。 真っ当な説明を求める方は二重スリット実験の真相を参照のこと。 真っ当な説明を動画で手っ取り早く見たい方はYouTubeへどうぞ。
尚、ノーベル物理学賞を受賞した朝永振一郎氏による光子の裁判も、科学的には間違っていないが、粒子性と波動性を混同した説明により疑似科学的誤解を産む一端を担っている。
当サイトの科学項目の目的も参照のこと。
科学で扱える現象の範囲
科学で扱うためには、同じ条件では同じ現象になる(同じ数式で記述できる)ことが必須の前提となる。 その前提が崩れれば、科学法則が成立しないし、実験の再現性も失われる。 よって、科学法則を見出したり、実験で結果を確かめるためには、この前提が崩れてはならない。 言い換えると、同じ現象にならない(同じ数式で記述できない)ケースを科学で扱うためには両者には違う条件が必要となる。 尚、量子力学は確率的に結果を推定する理論であるので、ここで言う「現象」には確率も含む。
オッカムの剃刀
実験結果を説明するために不要な仮定は置かない。 必要のない仮定を置いても、理論的考察の役にたたない。 無駄に話を難しくすれば、間違いを生みやすくなる。 メリットが全くなく、かつ、デメリットしかない不要な仮定は可能な限り排除すべきだろう。
実験セット
二重スリット実験では、一度別れた後に再び合流するような経路を設け、そこに位相の揃った波を通して干渉縞を観測する。 光の二重スリット実験では、基本原理通りに、光路を遮る衝立に平行な2本の切り込み(スリット)を設けて、その先のスクリーン上で干渉縞を観測する。

電子の二重スリット実験では「スリット」ではなく電子線バイプリズムが用いられた。
これは、1ミクロンの金属糸で左右の経路を分断したものであり、金属糸がプラスに荷電してマイナス荷電の粒子の軌道を中央寄りに曲げる働きがある。
マクロの(巨視的)世界
以下、人間が視認できる大きさで実験する。
マクロの単一スリット
人間が視認できる大きさの粒子を多数射出すると単一スリットでは次のような結果が得られる。

人間が視認できる波を射出すると単一スリットでは次のような結果が得られる(尚、明るさはエネルギーに比例する)。

波の場合は、粒子と違い、横に広がる。
マクロの二重スリット
人間が視認できる大きさの粒子を多数射出すると二重スリットでは次のような結果が得られる。

人間が視認できる波を射出すると二重スリットでは次のような結果が得られる(尚、明るさは…以下同文)。

波の場合は、粒子と違い、横に広がったうえで、干渉縞が生じる。
ミクロの(微視的)世界
以下、電子や光子を射出して実験する。
多数粒子射出
ミクロの単一スリット
粒子10万個相当(あまりに数が多すぎると肉眼では輝点が潰れてグラデーション状に見えるので、輝点が判別可能で、かつ、確率分布が良く分かる程度の数にした)の単一スリット実験では次のような結果が得られる。

電子線バイプリズムを用いた実験では、単一スリットは中央ワイヤーがない状態に相当し、その状態での粒子10万個相当の結果は次のようになる。

ミクロの二重スリット
粒子10万個相当の二重スリット実験では、次のような結果が得られる。

粒子10万個相当の電子線バイプリズムを用いた実験では、次のような結果が得られる。

トンデモ説明では、この後、何を確認するのか論点整理しないままいきなり単一粒子射出の話に進むのだが、ここではその前にきちんと論点を整理しておく。
この実験結果は、波動性を持たない粒子でも粒子性を持たない波でも説明できない。 しかし、波動性と粒子性を併せ持つなら説明可能である。(波動性と粒子性の二重性)
粒子性を持たない波では、輝点のない滑らかなグラデーションになるはずであり、輝点の密度で濃淡が表現されるこの実験の結果は説明できない。


では、波動性を持たない粒子ではどうなるか。 まず、原理通りの実験装置では、2つのスリットを通った電子の経路が交錯しないので、スリットの形に応じた2本の線しかできないはずであり、この実験の結果は説明できない。

ただし、実験セットのスケールが適切に設定されていれば、スリットの間隔等に比べて着弾を表示する点(以下、「輝点」)の直径の方が遥かに大きいため、実際には、2本の線はくっついてしまい、2本あることを判別することはできない。
一方で、電子線バイプリズムを用いた実験では、2つの経路が交錯するので、一定確率で電子同士が衝突し、軌道が変更されることが予想される。 しかし、それによって干渉縞が生じることは理論的にあり得ない。
顕微鏡等の光学機器メーカーのオリンパスによると肉眼で見える限界は0.1mm程度のようである。
肉眼で見える大きさは0.1mm(100μm)程度、ちょうど細い髪の毛の太さぐらいである。これ以下のものは肉眼で見ることはできない。
距離や視力によってはもう少し小さいものも肉眼で判別できるかもしれないが、極端な近距離での観察を除外し、かつ、個人差の影響を受けない範囲に限れば、概ね0.1mmと考えて良いだろう。 よって、輝点が0.1mmより小さければ肉眼では見えないことになる。 実際には肉眼で見えているから、輝点の直径は0.1mm以上あると考えられる。 輝点の集合体であることが判別できるなら、輝点の平均間隔は輝点の直径よりも大きいはずである。 尚、干渉縞のような場合、輝点の密度が高い部分でも輝点の集合体であることが判別できるなら、輝点の平均間隔はもっと大きくなる。
一方で、電子の大きさはどれくらいだろうか。 電子の大きさについては、現在、明確にはわかっていない。 電子の大きさに関連するとされる数値も様々なものがある。 ここでは、光の散乱を想定したトムソン散乱断面積(約6.65×10-29m2)を参考に用いる。 球形を前提とすると面積から直径は約9.2×10-15mと計算できる。 輝点の平均間隔が0.1mm=1×10-4m以上あるとすると、輝点の平均間隔は電子の直径の1億倍以上あることになる。 また、多数粒子を射出すると言っても、完全に同時に射出するわけではないので、実際には奥行方向にも間隔がひろがることになる。 以上を踏まえると、実験空間上での電子の密度はスカスカであると言える。 このようなスカスカ状態では、電子同士が衝突することは極めて稀であろう。
ただし、電子は荷電粒子であるため、電子同士が直接接触しなくても、クーロン力で反発し、軌道に影響を与える。 とはいえ、電子は極めて高速に射出されるため、ちょっとやそっとの力では目に見えるほどの大きな軌道変化にはならない。
これらの電子は、5万ボルトに加速されています。 すなわち、光の速度の約40%であり、毎秒12万キロメートル、一秒で地球の周りを3周も回る速度です。 長さ1メートルの電子顕微鏡の中は、1億分の1秒で、あっという間に通過してしまいます。
クーロン力は距離の2乗に反比例するので、電子同士がかなり接近しなければ、クーロン力による影響は無視できるだろう。 実験空間上での電子の密度がスカスカすぎることを考慮すると、無視できないほど大きく軌道を変化させる確率は極めて低いと予想できる。
仮に、軌道変化が生じる確率を大きめに見積もったとしても、射出方向の確率が一様であるなら、軌道が変化した場合の確率もほぼ一様と予想されるため、干渉縞が説明できない。 電子同士の衝突やクーロン力による反発以外の第三の要因があると仮定しても、それでは干渉縞が縦縞になることや等間隔(完全な等間隔ではないが実験装置のスケールではほぼ等間隔と言って差し支えない)になることが説明しづらい。
以上から、電子線バイプリズムを用いた実験において、波動性を持たない粒子では、中央ワイヤーがない場合と同様に、ほぼ一様な確率分布となるはずであり、やはり、この実験の結果は説明できない。

つまり、単一粒子射出で実験するまでもなく、多数粒子射出でも既に次のいずれでも説明のつかない結果が出ているのである。
- 波動性を持たない粒子
- 粒子性を持たない波
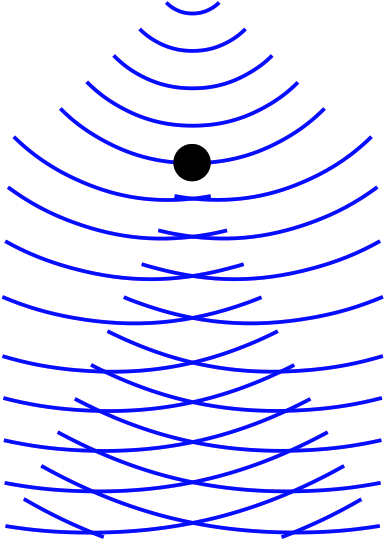
この結果は、電子や光子が、波動性と粒子性を併せ持つからだと考えるのが最も自然であろう。 二重解の理論とその派生理論では、波動性が粒子軌道に影響を与えることでこの実験結果を見事に説明している。
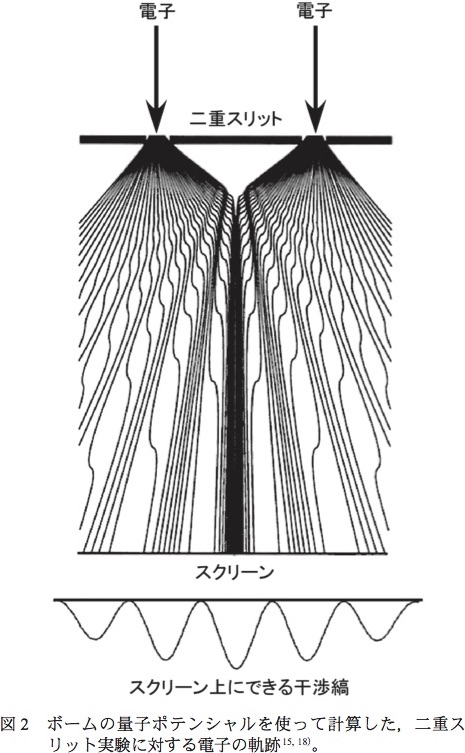
波動関数のわかりやすい説明(林久史) - 日本女子大学 理学部 物質生物科学科
単一粒子射出
ここで、単一の粒子でも波動性を併せ持つのかどうかが次の課題となる。 尚、波動力学で原子モデルを説明するためには、単一の粒子でも波としての性質が必要になる。 また、光についても単一の粒子でも波の性質を示すと考えられていた。
問題は、波のような性質をもたらすほど光子の数は多くないことである。
つまり、ある一瞬には、室内の光子数は10の12乗個程度しかない。 これは、1立方ミリメートル当たり10個程度ということであり、空気分子が10の16乗個程度であるのと大きな違いである。
「量子力学の解釈問題―実験が示唆する『多世界』の実在」(ISBN-10:4062576007,ISBN-13:978-4062576000,著:ColinBruce,訳&注:和田純夫)P.35
空気分子の数と比べて論じるのは乱暴なので、もう少し補足説明する。 「1立方ミリメートル当たり10個程度」を単純計算すると、光子と光子の平均間隔は0.46mmくらいであろうか。 それに対して、可視光線で最も長い波長は約800nmである。 以上により、この場合の光子と光子の平均間隔は波長の575倍となる。 常識で考えれば、複数の粒子が波を形作るなら、粒子と粒子の平均間隔は波長よりかなり短くなければならないはずである。 しかし、実際の光子と光子の平均間隔は波長の500倍以上も開いている。 これでは、複数の粒子が波を形作るとは考えにくい。
このように、かなり以前から、単一の粒子でも波の性質を示すと考えられていたようだ。 この推論を具体的に裏付ける実験が単一粒子射出の二重スリット実験である。
粒子がほぼ1個ずつ射出されるように実験装置を調整した結果、二重スリット実験では、次のような干渉縞が得られた。

同様に、粒子がほぼ1個ずつ射出されるように実験装置を調整した結果、電子線バイプリズムを用いた実験では、次のような干渉縞が得られた。

これは、単一の粒子であっても波動性と粒子性を併せ持つことを示している。
| 量 | 大きさ | |
|---|---|---|
| 粒子 | 分割可能な最小単位を持つ(量子性) | ある一定以下の大きさを持つ(局在性) |
| 波 | いくらでも細かく分けられる(連続性) | 任意に大きさを変えられる |
参考:初めて学ぶ物理学 量子論 by 筑波大学物理学系素粒子理論研究室金谷和至教授
1点に集約される性質と、空間的な広がりを持つ性質が両立する…とは、何とも奇妙な話である。 しかし、二重スリット実験の結果は、1点に集約される性質と、空間的な広がりを持つ性質が両立することを示している。
通過スリット特定
トンデモ説明ではこの段階で通過スリットの数を論じ始める。 しかし、それは、適切な論点整理ができていないが故の、迷走する考え方である。
ここで真っ先に論じるべきことは、通過スリットの数ではなく、波動性の有無である。 干渉縞が生じるための条件は複数ある。 そのうち、波動性以外の条件は実験環境によって左右される。 純粋に電子や光子が持つ性質だけで決定される条件は波動性だけである。 つまり、電子や光子が波動性を持たなければ、実験環境をどう変化させようとも、後から波動性を生み出すことはできない。 他の条件は実験環境を変えることで成立させる余地があるが、波動性だけは実験環境でどうにかすることができない。 だから、最も重要な条件は波動性の有無であり、それを真っ先に論じなければならない。
そして、波動性の有無を論じれば、通過スリットの問題も自動的に解決する。 というのも、波は空間を広がって伝搬するからである。 空間を広がって伝搬すれば、極めて間隔の狭い2つのスリットの両方を通らないと考える方が不自然である。 そして、干渉縞が生じているのだから、波が2つのスリットを通ることは疑う余地がない。 ある仮定が容易に実現できて、かつ、その仮定が正しい時だけに辻褄が合うなら、その仮定を疑う理由は何もない。 というように、波動性があれば、何の問題も残らない。
一方で、通過スリットの数が幾つであろうとも、波動性がなければ干渉縞が生じない。 通過スリットの数に結論が出ても、それだけでは条件が不十分であり、干渉縞が成立しない。 以上のとおり、どちらを真っ先に論じることが解決の近道であるかは一目瞭然だろう。
- その論点だけで自動的に万事解決する論点=波動性の有無
- その論点だけでは問題が解決しない論点=通過スリットの数
ようするに、波動性の有無より先に通過スリットの数を論じることが迷走の第一歩なのである。
「粒子が2つのスリットを同時に通った」とする根拠は皆無
トンデモ説明ではこの段階で「粒子が2つのスリットを同時に通った」などと言い出す。 そのような奇怪な仮定を何のために導入するのか意味不明である。 干渉縞は、波動性が作り出したものであって、粒子性が作り出したわけではない。 干渉縞の構成要素が輝点であることは粒子性によるものだが、干渉縞の密度の濃淡は波動性が作り出したものである。 だから、干渉縞が生じた事実をもってしても、そのような変わった粒子を想定する理由にはならない。 干渉縞の生成を説明するためには、粒子の着弾場所が干渉縞風の確率分布に従うことを説明する必要がある。 しかし、「粒子が2つのスリットを同時に通った」としても、その説明ができるわけではない。
百歩譲って、仮に、粒子が2つのスリットを通ったと仮定するなら、常に、輝点は2つセットで現れるはずである。
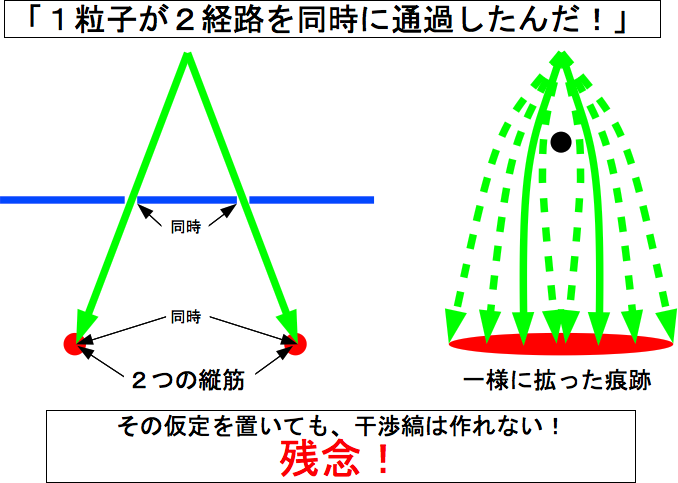
しかし、実際には、輝点は同時に1つしか現れない。 だとすると、実際に現れた輝点とペアになるもう片方のスリットを通った粒子はどこに消えるのだろうか。 その答えはDr.Quantumによる二重スリット実験トンデモ解説や粒子が2つのスリットを通ったと主張する人たちの描く図にある。 それらの図では、なんと、2つのスリットを通った粒子は常に同じ場所に誘導されるように描かれている。 しかし、粒子が干渉縞風の確率分布に誘導される作用が働くなら、粒子が2つのスリットを通らずとも干渉縞の発生を説明できる。
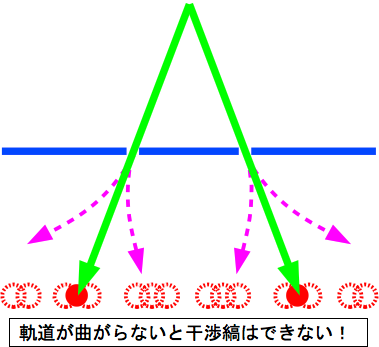
そして、そうした誘導作用がなければ、粒子が2つのスリットを通ったとしても、干渉縞が生じる余地はない。


さらに言えば、粒子が2つのスリットを通ったとしても、そうした誘導作用を説明することはできない。 つまり、粒子が2つのスリットを通ったと考えなければならない理由が存在しないのである。 しかも、粒子が2つのスリットを通った仮定すると、粒子が干渉縞を描く場所に誘導される作用の他に、2つのスリットを通った粒子が常に同じ場所に誘導されるという、より奇妙で説明困難な作用を想定しなければならない。 以上まとめると、次のようになる。
- 粒子が2つのスリットを通ったと考えなければならない理由が存在しない
- 粒子が干渉縞風の確率分布に誘導される作用があれば、干渉縞の説明には事足りる
- 粒子が干渉縞風の確率分布に誘導される作用がなければ、干渉縞を説明できない
- 粒子が2つのスリットを通ることは、その誘導作用とは全く無関係
- 粒子が2つのスリットを通ったと考えると、単一スリット通過にはない説明困難な作用が必要となる
- 2つのスリットを通るなら、2経路の粒子が常に同じ場所に誘導される作用を想定しなければならない
- 粒子が一方のスリットを通った場合には、常に同じ場所に誘導される必要はない
ある仮定が正しいと考える理由がなく、かつ、その仮定が説明困難な作用を必要とするなら、その仮定を棄却することが科学的に正しい推測である。 よって、粒子が2つのスリットを通ったとする仮定は棄却される。 以上の通り、「粒子が2つのスリットを同時に通った」という発想の元になる物が何もないし、そう考えても何の辻褄も合わせられず、余計に説明困難なことを増やしてしまう。 それなのに、何故、「粒子が2つのスリットを同時に通った」などと言い出すのか、全く意味不明である。
そして、トンデモ説明では、唐突に、「どちらのスリットを通ったか確かめる」と言い出す。 しかし、どのような条件で何の通過スリットを特定するのかは明確にしない。 このページでは、当然、どのような条件で何の通過スリットを特定するのか論点を明確にする。
二重スリット実験では、波の通過スリットを特定する意味はない。 何故なら、波が一方のスリットしか通過しないなら、二重スリット実験の条件を満足せず、当然のごとく干渉縞が生じないからである。 実験の過程を検証したいなら、実験の前提を維持しなければ意味がない。 実験の前提が覆っては、実験過程の検証にはならないのである。 だから、二重スリット実験では、波が二つのスリットを通過する条件を維持しなければならない。 波が二つのスリットを通過する条件が維持されるなら、当然、波は両方のスリットを通るはずである。 であれば、波の通過スリットを特定する意味はない。 以上のことから、二重スリット実験で通過スリットを特定すべきなのは波ではなく粒子である。 二重スリット実験の条件を維持する限り、波の通過スリットを特定できるわけがない。 二重スリット実験で特定可能なのは粒子の通過スリットだけである。 この整理がきちんとできていないと頓珍漢なことになる。
詳細は二重スリット実験の真相に記載するが、次のいずれの方法でも、粒子の通過スリットを特定しようとすると、波長等の波の性質に致命的な影響を与えるため、二重スリット実験の前提を維持できない。
- ファインマンの思考実験
- 反跳運動量
- 片側検出器
- 運動量に「影響しない」監視装置
言い換えると、二重スリット実験の前提を維持する限り、粒子の通過スリットを特定できない。 また、片側経路屈折方式や後測定方式では、波長等の波の性質に致命的な影響を与えないが、粒子の通過スリットを特定する実験セットになっていない。 干渉分離方式では、経路測定による擾乱を補正できる場合は、補正前のデータに干渉縞が生じていなくても、実験をやり直さずに取得済みのデータを補正するだけで干渉縞を取り出すことが可能である。 このことは、干渉縞が生じない場合も波としての干渉が生じていることを示唆している。 ただし、経路情報と補正情報はどちらか1つしか得ることができないという相補性が成立している。
以上から、結論として言えることは、粒子の通過スリットを特定する有効な方法はないということである。 当然、「粒子が2つのスリットを同時に通った」などという奇怪な仮説を証明できないことは言うまでもない。
経路を特定しても2本線にはならない
ちなみに、マクロの物質と相互作用を起こすような経路測定方法を用いない限り、経路測定段階では射影仮説を適用できず、スクリーンに到達するまでは波が1点に凝集することはない。 仮に、経路を測定した時点で波が一点に凝集するとしても、ハイゼンベルクが論文「量子論的運動学および力学の直観的内容について」で指摘した通り、凝集状態を持続的に維持することはできないため、スクリーンに到達するまでの過程で波は時間とともに広がってしまう。 結果、経路を特定する場合は、次のような結果になり、前述のような波動性を持たない粒子特有の2本線になることはない。

もしも、粒子特有の2本線になるとすれば、シュレーディンガーの提唱した波動一元論が正しいことになる。 波動一元論が正しければ確率解釈は無用の長物となり、量子力学の標準理論は根底からひっくり返ってしまう。 量子力学の標準理論が正しいと仮定するなら、粒子特有の2本線になることは絶対にありえない。
ネット上には2本線になると主張している事例が少なくないが、いずれも、説明者の想像に基づいた図は書かれていても、実験データを全く示していない。 その証拠に、理論上の確率分布と一致しない、手作業で作成したとしか思えない様な雑な図しか示されていない。 実験データや正確な計算でシミュレーションした場合は、このような雑な図になろうはずもない。 また、2本線の間隔が理論上予測される間隔に比べて極端に大きすぎることも実験データではないことを示している。
通常、スリット間隔は1μm〜数10μmで、放射源からスリットまで、または、スリットからスクリーンまでの距離は数10cm〜1m程度である。 肉眼で観測可能な干渉縞を描こうとするなら、スリット間隔はあまり広くできないし、放射源からスリットまで、または、スリットからスクリーンまでの距離もあまり小さくできない。 ここで放射源とスリットを結んだ直線上の経路を通ると仮定すれば、2本線の間隔は非常に狭いものとなる。 一方で、顕微鏡等の光学機器メーカーのオリンパスによると肉眼で見える限界は0.1mm程度のようである。
肉眼で見える大きさは0.1mm(100μm)程度、ちょうど細い髪の毛の太さぐらいである。これ以下のものは肉眼で見ることはできない。
言い換えれば、2本線が肉眼で見えているなら、それらの線の太さは0.1mm(100μm)程度以上あるはずである。 以上を踏まえると、2本線の間隔を広めに見積もっても次の様な図にしかならないはずである。

少なくとも、これよりも2本線の間隔が広い場合は、説明者の想像に基づいた図であることを疑う余地はない。 尚、遅延選択量子消しゴム実験は、経路を特定する場合の実験データが示されている少ない例だが、2本線にはなっていない。
経路を特定しても波動性は失われない
なんと、トンデモ説明では、通過スリットを特定できないことを説明した後、唐突に次のように言い出す。
- 「経路を特定する実験セットにしたとき(見ているとき)は波動性が失われる」
- 「経路を特定しない実験セットにしたとき(見ていないとき)は粒子性が失われる」
前者は、おそらく、干渉縞が生じないことが波動性が失われた証拠だと誤認しているからだろう。 確かに、経路を特定する実験セットでは干渉縞が生じない。 しかし、それは波動性が失われた証拠にはなり得ない。 よく勘違いする人がいるが、ある命題が真であることは、対偶も真であることを保証するが、裏や逆が真であることを保証しない。
- 元の命題
- 「干渉縞が生じれば波動性がある」=真
- 対偶
- 「波動性がなければ干渉縞は生じない」=真
- 裏
- 「干渉縞が生じなければ波動性はない」=以下で検証
- 逆
- 「波動性があれば干渉縞が生じる」=以下で検証
これは論理学の基礎である。 裏が真であるかどうかを知るには、元の命題ではなく、裏や逆(裏と逆はお互いに対偶関係になっている)を検証しなければならない。 では、裏「干渉縞が生じなければ波動性はない」は成立するか。 干渉縞が生じるためには、次の全ての条件を満足しなければならない。
- 波動性がある
- スクリーンの位置に応じて経路差が変化する
- 双方の波の偏波(偏光)が揃っている
- スクリーンの位置と経路間位相差が一対一で対応している
- 実験セットの位置関係が安定している
- 波の波長が安定している
- 波の位相が安定している(単一粒子射出の場合は経路分岐後に限る)
- 実験セットのスケールが適切に設定されている
1つ目の条件は言うまでもない。 もちろん、1つ目の条件が成立しなければ、他の条件も成立しない。
2つ目の条件が成立しない場合として、例えば、2つのスリットからの距離差が等しい所に(双曲線状に)スクリーンを配置すれば、経路差が定数となって干渉縞は生じない。
3つ目の条件が成立しない場合として、偏波(偏光)が完全に直交している場合や逆方向の完全円偏波(偏光)である場合等が考えられる。 その場合、両者の強度が等しければ、干渉結果は偏波(偏光)の形(直線、楕円、円)や向きにのみ現れ、合成波の強度は変化しない。 結果として、干渉は生じても干渉縞は生じない。
4つ目の条件が成立しない場合は、同じ場所で強め合う干渉縞と弱め合う干渉縞が互いに相殺しあって、干渉縞が見えなくなる。 この条件が成立しない一例として、サブの3条件のいずれかが成立しない場合が考えられる。 理論的にはそれ以外の状況でも3つ目の条件が成立しない場合があるが、かなり特殊な状況となるので考慮する必要はなかろう。
さらに、5つ目の条件が成立しないと、目視では干渉縞を観測できなくなる。 例えば、スリットの間隔が広すぎたり、スリットからスクリーンまでが近すぎると干渉縞の間隔が小さくなりすぎて肉眼では見えなくなる。 逆に、干渉縞の間隔が広すぎると、スクリーンに表示される範囲では強度変化が観測できなくなることもある。 こうしたスケールのミスは、結果を具体的計算で予測していない場合に犯しやすい。
これらの条件が1つでも崩れると干渉縞は生じない。 つまり、波動性があっても、他の条件が1つでも崩れると干渉縞は生じない。 波動性があっても干渉縞が生じないケース、言い換えると、干渉縞が生じないのに波動性があるケースが存在するなら、干渉縞が生じないことは波動性がない証拠とならないことは明らかだろう。 つまり、干渉縞が得られないことは、波動性の肯定的証拠が得られないことを示しているだけであって、否定的証拠が得られたことを意味しない。 干渉縞が生じることは波動性の有力な証拠となる。 しかし、ここで説明したとおり、干渉縞が生じないことは波動性がない証拠にはならないのである。 J.Wheelerの遅延選択実験等の結果からは、粒子の経路を特定するかどうかに関わらず、波動性が現れていることが明らかである。 例えば、遅延選択量子消しゴム実験において、粒子の経路を特定可能な実験セットにすると、二つの経路の位相関係が乱されて、干渉縞が見えなくなる。

ただし、この実験セットでも、粒子の経路情報を検出しなければ(粒子の経路情報を検出した後では手遅れ)、位相の乱れの量の情報(D1と相関する場合は位相の乱れが±90度未満、D2と相関する場合は位相の乱れが±90度以上、各記号の意味および原理説明は遅延選択量子消しゴム実験を参照)を得ることができる。 位相の乱れの量の情報に基づいてR01(D0の検出結果のうちD1と相関する結果のみを抽出したもの)を分離抽出すると次の干渉縞が現れる。

同様にR02(D0の検出結果のうちD2と相関する結果のみを抽出したもの)を分離抽出すると次の干渉縞が現れる。

これは、2種類の干渉縞が相殺しあって見えなくなっていること、すなわち、水面下で波の干渉が起きていることを示唆している。 ただし、粒子の経路情報を断念しなければ、位相の乱れの量の情報を得ることができない。 いずれにせよ、干渉縞が観測できないにも関わらず水面下で波の干渉が起きているケースがある以上、干渉縞が観測できないことが波動性が失われた証拠にはならないことは明らかである。 よって、「経路を特定する実験セットにしたとき(見ているとき)は波動性が失われる」と考える理由は全くない。
経路を特定しなくても粒子性が現れる
後者の「経路を特定しない実験セットにしたとき(見ていないとき)は粒子性が失われる」仮定に至っては、そのような奇怪な仮定を何のために導入するのか意味不明である。 そもそも、実験では輝点の密度の濃淡によって干渉縞が生じているのだから、経路を特定しない実験セットにしたときにも明らかに粒子性の発現が見て取れる。 経路を特定するか否かに関わらず、マクロと相互作用を起こす測定を行う以上は、必ず、粒子性が発現するのである。
まとめ
この実験では、少なくとも、スリットを出てからスクリーンに到達するまでは波の性質を持つ必要があるが、それ以外での波の性質の有無を問う必要がない。 また、この実験では、少なくとも、スクリーンに到達してから結果を観測するまでの間に粒子の性質を持つ必要があるが、それ以外での粒子の性質の有無を問う必要がない。 以上の通り、経路を特定する実験セットにしたときに波の性質を失うと考える必然性はないし、経路を特定しない実験セットにしたときに粒子としての性質を失うと考える必然性もない。 そして、経路を特定するかどうかによって波になったり粒子になったりするという仮定を置いても、実験結果を説明するうえでは全く何の役に立たない。 つまり、経路を特定するかどうかによって波になったり粒子になったりするという発想の元になる物が何もないし、そう考えても何の辻褄も合わせられない。 経路を特定するかどうかによって波になったり粒子になったりすると仮定するとJ.Wheelerの遅延選択実験や遅延選択量子消しゴム実験等と辻褄が合わない。 それなのに、何故、「経路を特定する実験セットにしたとき(見ているとき)は波動性が失われ、経路を特定しない実験セットにしたとき(見ていないとき)は粒子性が失われる」などと言い出すのか、全く意味不明である。 このような全く必然性のない奇怪な仮説を持ち出して、かつ、実験結果がその仮説と整合しないときに更なる奇怪な仮説(「未来が過去を変えた」等)を持ち出すことは疑似科学特有の特徴である。 当然、「経路を特定する実験セットにしたとき(見ているとき)は波動性が失われ、経路を特定しない実験セットにしたとき(見ていないとき)は粒子性が失われる」などという奇怪な仮説を証明できないことは言うまでもない。
ちなみに、コペンハーゲン解釈では、測定していないとき(マクロとの相互作用がないとき)に物理的にどうなっているかは追求しないことになっている。 しかし、そこで採用されている標準理論の数式上の処理では、測定していないとき(マクロとの相互作用がないとき)は空間に広がった波であり、測定しているとき(マクロとの相互作用があるとき)も粒子状に凝集した波である。 この場合、測定していないとき(マクロとの相互作用がないとき)は粒子状に凝集していないという意味で粒子性を持たないが、測定しているとき(マクロとの相互作用があるとき)も波動性を持っている。 一方、隠れた変数理論では、常に波動性と粒子性を併せ持つ。 このように、量子力学の解釈のうち、真っ当なものに限れば次のようになる。
- 測定によって粒子性の有無が変わるとする解釈はあっても、経路を特定するかどうかで性質が変わるとする解釈はない
- どの解釈でも波動性は常時持ち続けており、一時的にでも波動性を失うとする解釈はない
最後に
量子力学の実験結果には古典力学に適合しないものがある。 しかし、二重スリット実験の結果には、古典力学に適合しない性質は見られない。 既に説明した通り、二重スリット実験の結果だけで良ければ、その他の実験結果について説明しない限り、古典力学の枠組みで十分に説明可能である。
誤った説明の例
以上の説明を次のようなトンデモ解説と比較してもらいたい。
- Dr.Quantumによる二重スリット実験トンデモ解説
- ネット上の二重スリット実験トンデモ解説
- 論理破綻例(「哲学的な何か、あと科学とか」 )
- 何と言うかアレ(南●さん)
- 「二重スリット実験を批判」?
- 「波長がずれるだけで二本線にはならない」?
- このページの参照元
科学 疑似科学を批判する疑似科学 J.Wheelerの遅延選択実験 二重スリット実験の真相 Dr.Quantumによる二重スリット実験トンデモ解説 ネット上の二重スリット実験トンデモ解説 波動性と粒子性の二重性
このページへのご意見は節操のないBBSにどうぞ。
総合案内
科学一般
疑似科学等
- 疑似科学
- 数学や科学への無理解
- 疑似科学を批判する疑似科学
- STAP細胞論文捏造事件
- CCS地震原因説
- 地球温暖化懐疑論
- 疑似科学者列伝