二重スリット量子消しゴム検証実験の提唱

• はじめに
• Double-slit quantum eraser（量子消しゴム実験）の検証実験
  • 実験手法
  • 結果の解析
  • 実験の解説
  • 補足
  • まとめ
• メイキング・オブ・検証実験

はじめに 

このページで説明する実験手法に関する知的財産権は放棄するものとする。 二次的利用についても同様とする。

Double-slit quantum eraser（量子消しゴム実験）の検証実験 

量子力学のある種の実験において、どちらの経路を通ったかを示す目印＝Which Path Marker(以下、「ＷＰＭ」)を付けると、実際にＷＰＭを観測しなくても、干渉縞が生じなくなるとされている。

しかし、二重スリット量子消しゴム実験にも書いた通り、「ＷＰＭ」が本当にＷＰＭとして機能するのかどうかは眉唾物である。 もしも、ＷＰＭとして機能するのであれば、いずれか一つの経路の波が射影仮説による「波束の収縮」後の可観測量を決めることになる。 それでは、二重スリット実験の真相で説明した通り、二重スリット実験の干渉縞が説明できなくなる。 干渉縞が生じるためには、可観測量が複数の経路の波の合成波で決定される必要があるが、それではＷＰＭとして機能し得ない。

以上の通り、「ＷＰＭ」が本当にＷＰＭとして機能するとは到底考え難い。 そこで、「ＷＰＭ」が本当にＷＰＭとして機能するかどうかを検証する実験を提唱する。

実験手法 

Double-slit quantum eraserの実験手法を一部流用する。

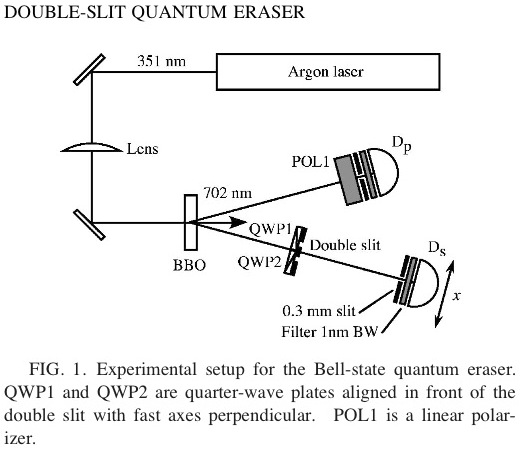
論文中のFIG.1の図を以下のように置き換える。

• POL1は使用しない
• QWP1,QWP2は偏光板に置き換え、それぞれの偏光方向を90°ずらす。

D_Pでは偏光の回転方向(量子力学的にはスピン)を検出する。 ただし、D_Sの検出結果と相関できないデータは破棄する。 その際、D_Sを少しずつ(x)ずらした状態で何度もデータを取り、横軸をx、縦軸を検出比としたグラフを描く。

結果の解析 

• x値に関わらず、検出比が常に50%:50%となるなら、「ＷＰＭ」がＷＰＭとして機能している。
• 検出比がx値によって変動するなら、「ＷＰＭ」はＷＰＭとして機能していない。

実験の解説 

「ＷＰＭ」がＷＰＭとして機能するならば、可観測量はいずれか一つの経路の波によって決定される。 ２つの経路上に置いた偏光板により、いずれの経路の波も直線偏光となる。 直線偏光は、同じ強さの逆回転の円偏光に分解できるので、偏光の回転方向(量子力学的にはスピン)の検出比は50%:50%となる。 以上により、「ＷＰＭ」がＷＰＭとして機能するならば、検出比は常に50%:50%となる。

可観測量が複数の経路の波の合成波で決定されるならば、当然、「ＷＰＭ」はＷＰＭとして機能しない。 ２つの経路の波の合成波は、２つの経路の距離差によって、右円偏光、左円偏光、直線偏光、あるいは、それらの中間の偏光(楕円偏光)となる。 右円偏光であれば右円偏光が100%検出され、左円偏光であれば左円偏光が100%検出される。 直線偏光であれば、先ほどの説明通り、検出比は50%:50%となる。 楕円偏光であれば円偏光と直線偏光の中間の検出比となる。 そして、２つの経路の距離差はx値によって決まるため、x値と検出比には相関関係が生じる。 この場合は、検出比がx値に応じて変動することとなる。 それは、ちょうど、次の図のような形となろう。

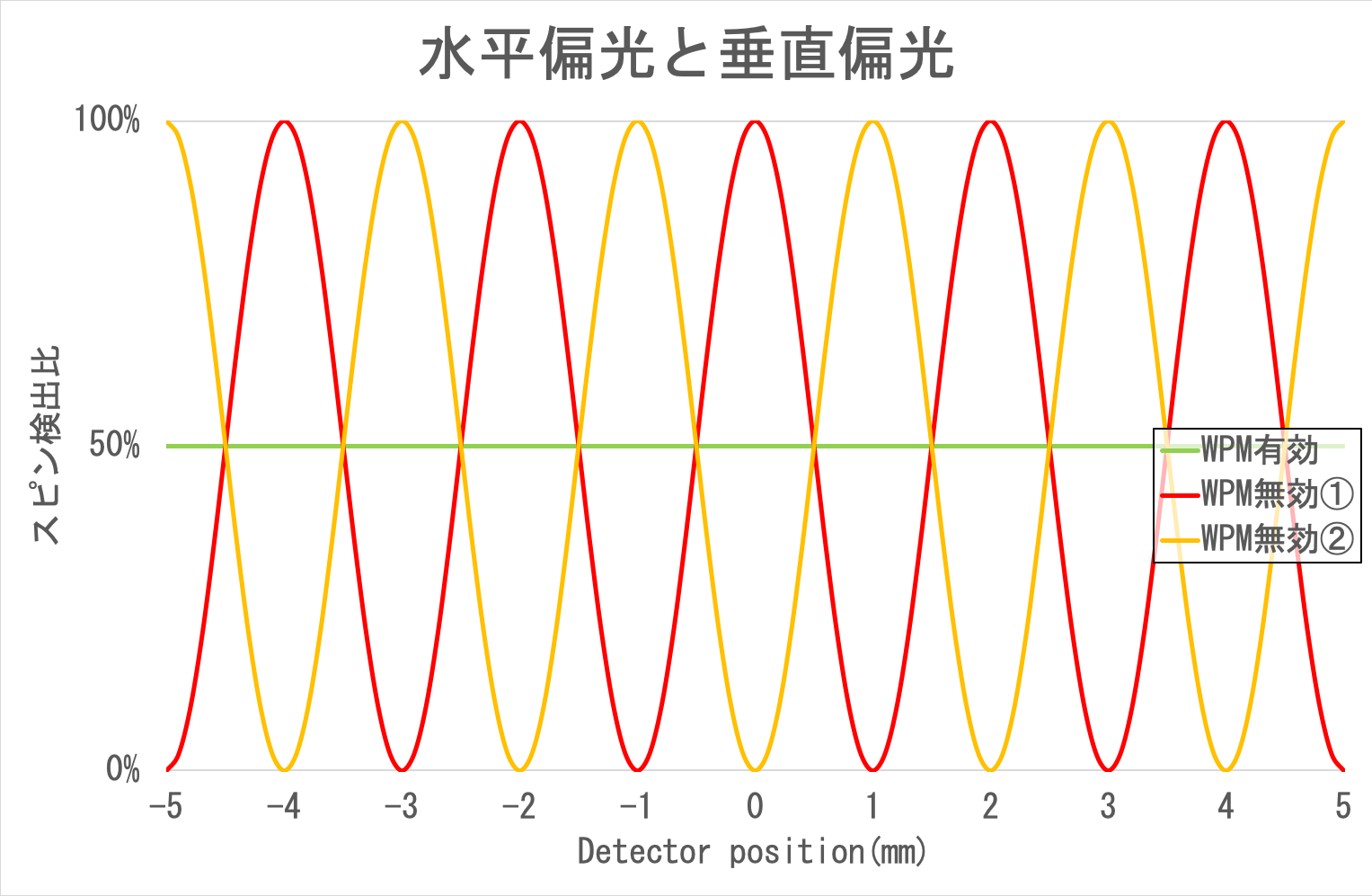
補足 

「この実験セットでは偏光フィルタを追加しないとＷＰＭは検出できない。 ということは、このこの実験セットではＷＰＭが付加されていない。 偏光フィルタを追加すると実験環境が変わるので検証にならない」 と実験の不備を指摘する人がいるかもしれない。 それならば、「ＷＰＭ」を逆向き円偏光と直交直線偏光の中間的偏光にすれば良い。

ここで「ＷＰＭとして機能するのは円偏光の時だけで、楕円偏光ではダメだ」と言い出す人がいるかもしれない。 しかし、それは、二重スリット量子消しゴムは、現実には実現不可能だと認めているに等しい。 というのも、現実には全く歪みのない完全な円偏光で実験することはできないからである。 たとえば、wave plateの長さがほんの少し違うだけで、円偏光に歪みが生じる。 また、実験空間がわずかでもwave plateのような性質(偏光方向による伝搬速度の違い)を持っていれば、それによっても円偏光に歪みが生じる。 このような円偏光に歪みを生じさせる要因は多々考えられ、それによって、僅かながら偏光が楕円化してしまう。 だから、現実には、完全な円偏光ではなく、わずかに歪んだ楕円偏光で実験することになる。 ここで、もしも、楕円偏光では経路情報(Which Path Information)を得られないのであれば、現実的には「ＷＰＭ」が本当にＷＰＭとして機能しないことになり、この検証実験を提唱するまでもなくなってしまう。 逆に、二重スリット量子消しゴムが現実に可能だとするなら、スピンの検出確率に一定程度の差があれば楕円偏光でも差し支えないと考える必要がある。

例えば、双方のスリットを通過した光が、それぞれ、次のようになるよう細工する。

• 右回り水平楕円偏光
• 左回り垂直楕円偏光

これならば、偏向板を設けずとも左右の波をスピンで確率的に区別することが可能となる。 そして、左右の合成波は直線偏光か楕円偏光となる。 ここで、一方のスリットを通過した波のみの場合のスピンの検出比がＰ(%)：１００－Ｐ(%)であると仮定する。 尚、Ｐ(%)は、楕円が円に近いほど100%もしく0%に近づき、楕円が直線に近いほど50%に近づく。 この場合、測定結果がいずれか一方の波のみで決定されるなら次の結果になる。

• いずれかのスリットをＰ(%)の確率で通過したと特定できる
• x値毎の平均は、x値とは無関係に50%:50%となる。

測定結果が双方の合成波で決定されるなら次の結果になる。

• 通過スリットは確率的にも予測できない
• x値毎の平均は、x値によってＱ(%)：１００－Ｑ(%)から１００－Ｑ(%)：Ｑ(%)まで干渉縞風に変化する

仮に、Ｑが４０％か６０％であれば、次のようなグラフになる。

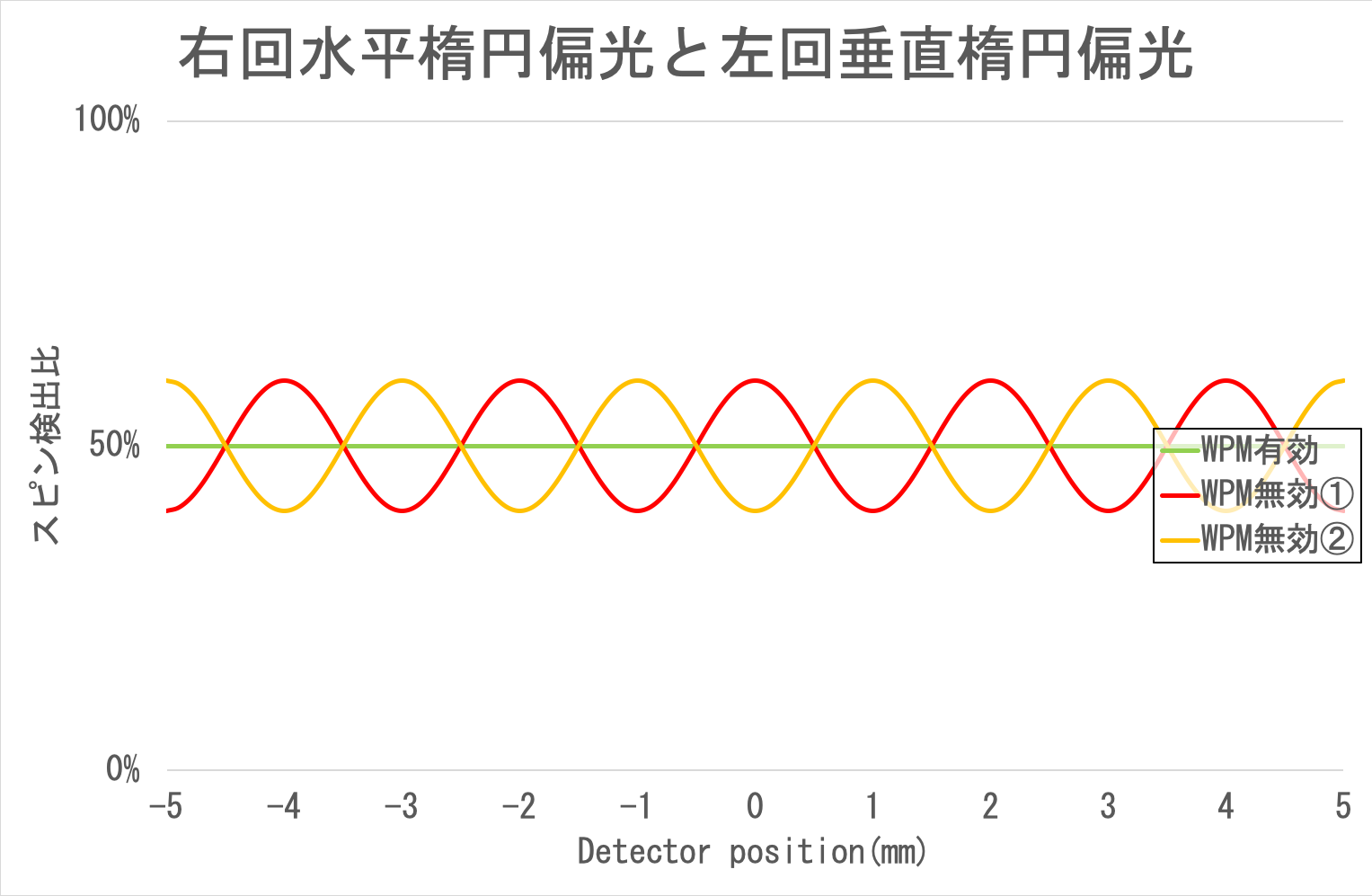
尚、Ｑ(%)は、Ｐ(%)とは逆に、楕円が円に近いほど50%に近づき、楕円が直線に近いほど100%もしく0%に近づく。 結果、完全な円偏光になれば、通過スリットの予測確率が100%になる一方で、その真偽、すなわち、本当にＷＰＭとして機能しているかどうかの検証は不可能になる。 逆に、完全な直線偏光になれば、通過スリットの予測確率が50%になる（つまり、全く予測できていない）。 完全な円偏光でも、完全な直線偏光でもない、楕円偏光であれば、通過スリットの予測確率はソレなりとなり、その真偽、すなわち、不完全ながらもＷＰＭとして機能しているかどうかの検証が可能となる。

まとめ 

この実験では、スピンの検出比だけでなく、合計検出頻度についてもグラフ化して、干渉縞が消えていることを確認する必要がある。 もしも、干渉縞が通常の二重スリット実験のように現れるなら、この検証実験は失敗である。 以下、干渉縞が消えていることを前提に説明する。

もしも、「ＷＰＭ」がＷＰＭとして機能していないなら、紛い物のなんちゃってＷＰＭでも干渉縞が消えていることになる。 つまり、本物のＷＰＭでなくても干渉縞が消えるなら、量子消しゴム実験が干渉縞とＷＰＭの因果関係の証拠とならないことを示している。 尚、その場合は、干渉縞としての模様が生じなくても偏光の形で干渉の痕跡が生じていることを示しているため、干渉縞を生じないことが「波の性質が失われた」ことを意味しないことも証明する。

もしも、「ＷＰＭ」がＷＰＭとして機能していたとすれば、二重スリット実験の干渉縞との理論的整合性を考える必要がある。 また、その場合は、干渉縞の有無とＷＰＭの因果関係についても、確定的に論じるには不十分であろう。

メイキング・オブ・検証実験 

Double-slit quantum eraserにおいて「ＷＰＭ」がＷＰＭとして機能するならば、 この実験の「簡易版」 とやらでも「ＷＰＭ」がＷＰＭとして機能するはずである。 ところで、「簡易版」ではＷＰＭをどのように検出するのだろうか…とぼんやり考えていた。 その前に「簡易版」ではどのような干渉が起きているか整理しなければと考えた所で、「簡易版」でフルセットの検出方法を使ったらどうなるかと思いついた。

「ＷＰＭ」がＷＰＭとして機能するならば、D_PやD_Sで一方の経路を通った光だけを検出しなければならない。 それならば、「簡易版」で同じ検出方法を用いても一方の経路を通った光だけを検出しなければおかしい。 そして、「簡易版」では、一方の経路を通った光は必ず直線偏光となる。 だから、「ＷＰＭ」がＷＰＭとして機能するならば、「簡易版」で同じ検出方法を用いた場合には、検出比が常に50%:50%となるはずである。

逆に、一方の経路を通った光だけを選別できず、両経路の合成を検出するとすればどうなるか。 先に述べた通り、両経路の合成は、場所により、円偏光だったり、楕円偏光だったり、直線偏光だったりする。 であれば、場所によって検出比が変化するはずである。

以上により、場所によって検出比が変化するかどうかを確認すれば、「ＷＰＭ」がＷＰＭとして機能するかどうかを確かめられる。 ということに気づいた。 ここまで約３分。 ほんの軽い思いつきであって、知的財産権を主張するほどの高度な思考結果ではない。 説明文をまとめるのに２時間くらいかかったかな？