二重スリット量子消しゴム実験(旧)

• 最初に
• 一般化した原理説明
  • 経路情報の付加
    • 概略
    • 経路印を付加する対象は波か？粒子か？
    • 経路を特定する対象は波か？粒子か？
  • 経路情報の消去
  • 干渉縞との関連性
  • 原理まとめ
• Double-slit quantum eraser（量子消しゴム実験）
  • 実験セットの説明
    • 基本実験装置
    • 経路情報の検出
    • POL1とQWP1とQWP2を置く
    • POL1なしにQWP1とQWP2を置く
  • 実験の解説
    • 経路情報について
    • 干渉について
    • まとめ
    • 簡易版？
• 誤った説明の例

最初に 

ここのページは二重スリット量子消しゴム実験の古いバージョンである。

一般化した原理説明 

二重スリット実験の真相で説明した二重スリット実験において、スリット通過時は経路印(which path marker)のみを付加してスクリーン直前で経路情報(which path information)を検出する方式、および、経路印を消去して通常の二重スリット実験に戻す原理について説明する。

経路情報の付加 

概略 

次の図のように、何らかのフィルター類を用いて、２つの経路を通過した後に経路印をつける。

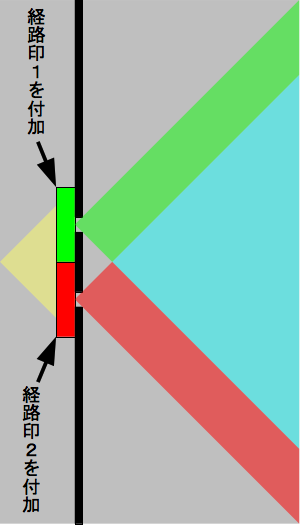
この経路印をスクリーン直前で検出すれば経路情報が得られる…というのが、スクリーン直前で経路情報を検出する理屈である。 経路印を付加した場合は、実際に経路情報を測定しなくても干渉縞が消えるとされる。 ただし、干渉縞が消えるだけであって、波の干渉がなくなるわけではない。

経路印を付加する対象は波か？粒子か？ 

スリットで経路印を付加する対象は、波なのか？それとも、粒子なのか？ 一般に、経路印として用いられるのは偏光等であるので、経路印を付加する対象は波であろう。

経路を特定する対象は波か？粒子か？ 

仮に、波の経路を特定するものとする。 二重スリット実験では、両方のスリットを通過した波がスクリーンに到達するので、スクリーン直前には両方の波の合成波が到達する。 だから、二重スリット実験の条件を満たしていれば、合成波には両経路の経路印が混じり合うことになる。 混じり合った２つの波を分離することはできないはずなので、スクリーンに到達した波の経路印は一方の経路だけの経路印とはならない。 もしも、検出結果が一方の経路の経路印を示すのであれば、その場合は次のいずれかのとおり、事実上、片方の経路が塞がれていることになる。

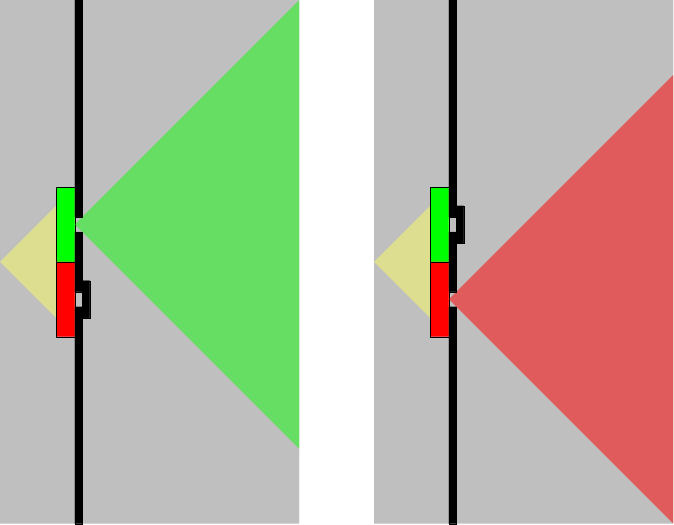
であれば、この方法では、二重スリットの条件を維持したまま経路情報を得ることができない。 単一スリットになるのであれば、経路を特定する意味はない。

仮に、粒子の経路を特定するものとする。 波に付加した経路印で粒子の経路が特定できると仮定するなら、粒子の通過した経路と同じ経路を通過した波のみによって可観測量が決まることになる。 一方、二重スリット実験では、両方のスリットを通過した波の合成波が、粒子の位置や運動量等の可観測量を決定する。 でなければ、干渉縞が説明できない。 片方のスリットを通過した何かだけで粒子の位置や運動量が決まるなら、干渉縞が生じる余地はない。 干渉縞が生じるためには、双方のスリットを通過した何かを合成したものが粒子の位置や運動量を決める必要がある。 そして、その「何か」とは言うまでもなく波である。 であれば、検出結果は、両方の経路を通過した波の経路印の影響を受けるはずであり、一方の経路のみの経路印を検出することはできないはずである。 それでは粒子の通過スリットを特定できない。

いずれにせよ、経路印を検出すれば経路情報を得られるという話は極めて疑わしい。 経路情報を得ることのできない見掛け倒しの経路印モドキを付加しているだけである。

経路情報の消去 

次の図のように、何らかのフィルター類を用いて、それまでに付加されていた経路印の内容に関わらず、いずれも同じ印が付加されるようにする。

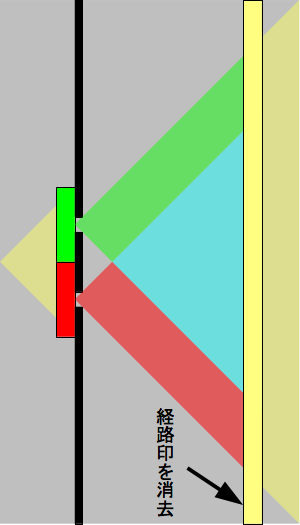
いずれも同じ印が付加されるということは、その印から経路を特定できなくなるので、経路情報を消去したに等しい。 この場合には、干渉縞が復活するとされる。

干渉縞との関連性 

一見すると、次のようにも見える。

• 経路印を付加すると干渉縞が消える
• 経路印を消去すると干渉縞が復活する

しかし、経路印なるものを付加しようとすれば、波のパラメータが変わるので、干渉結果に影響を与えるのは当然である。 しかも、干渉縞が消える場合も、波としての干渉が失われるわけではない。 後で説明する実験の「本格版」では直線偏光の偏光の向きとして、「簡易版」では円偏光か直線偏光か、及び、偏光の回転方向として干渉が生じる。 そして、その干渉は綺麗に揃った模様となっているはずである。 ただし、波の強度は干渉結果に関わらず一定となる。 通常の方法では、その干渉結果が視覚的に得られないから、干渉縞が観測できないだけに過ぎない。 二重スリット量子消しゴム検証実験の提唱に書いたようなやり方であれば、その干渉結果を視覚的に得ることができる。

つまり、経路印なるものを付加しようとしたことで、波のパラメータが変化し、その結果、干渉が波の強度変化以外に現れるようになっただけに過ぎない。 また、経路印なるものを消去しようとすると、さらに波のパラメータが変化し、その結果、また、干渉が波の強度変化に現れるようになる。 これは、経路印なるものが本当に経路印として機能しているかどうかとは関係がない。

原理まとめ 

この方法は、隠れた変数理論の検証としては、役に立たない。 というのも、隠れた変数理論の検証に用いるには、波が両経路を通過し、かつ、その波に影響を与えないよう、粒子の経路を特定する必要があるからである。

また、経路印を付加することと干渉縞の消失に因果関係があるのか、それとも、偶然そう見えるだけの現象なのかは、慎重に検討する必要があるだろう。

Double-slit quantum eraser（量子消しゴム実験） 

一部でDouble-slit quantum eraserが話題になっているようだ。 この実験は、経路特定と干渉消失の強い相関関係を示唆する目的の実験であるが、両者の因果関係を示唆する結果は出ていない。 何も知らない素人が見ると「経路特定が干渉消失の原因である」と誤読しかねないが、実験結果が意味することは逆である。

実験セットの説明 

基本実験装置 

図（論文中のFIG.1）にも示されているように、D_Sを少しずつ(x)ずらした状態で何度もデータを取っているため、横軸をx、縦軸を検出数としたグラフを描くことが出来る。 そして、このグラフが干渉パターンを描くかどうかが検証される。

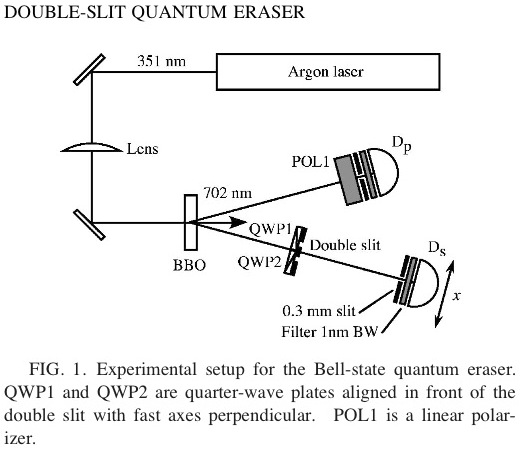
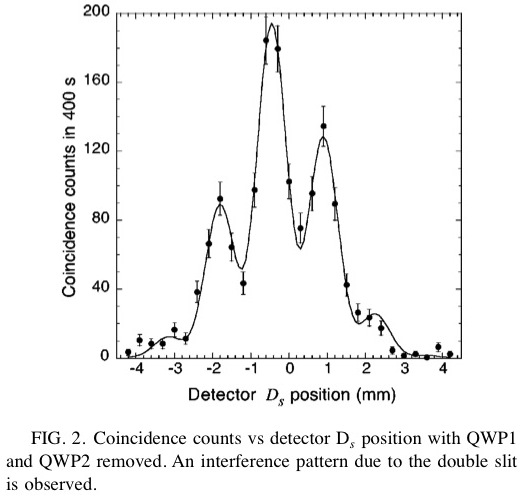
まず、POL1,QWP1,QWP2の全てがない状態では通常の二重スリット実験と同じとなる。 よって、グラフは典型的な干渉縞パターンとなる（論文中のFIG.2）。

経路情報の検出 

次の部分に実験セットの概要が説明されている。

QWP1 and QWP2 are quarter-wave plates with fast axes at an angle of 45°. The circular quarter-wave plates were sanded (tangen- tially) so as to fit together in front of the double slit.

Double-slit quantum eraserP.033818-5

wave plateは垂直偏波と水平偏波で速度が変わる光学装置であって、quarter-wave plateは位相シフトがπ/2となるwave plateを指す。

偏波(偏光)の垂直成分と水平成分の位相関係を操作すると円偏波(偏光)にしたり、楕円偏波(偏光)にしたり、直線偏波(偏光)にしたり、回転方向が逆の円偏波(偏光)にしたりできる。 その原理はそれほど難しくはないが、説明は非常に面倒である。 簡単に説明してみよう。 θを変化させると座標(cosθ,sinθ)は回転する。 このX成分とY成分の位相を変化させると、楕円運動になったり、線分運動になったり、逆回転になったりする。 以上で分からなくても、ネットで調べれば簡単に情報が見つかるだろう。 例えば、Wikipedia:偏光の「波長板」の所では結論だけ書いてある。 だから、ここではこれ以上は説明しない。

この実験セットでどのようにして経路情報(which-path information)を得るかは次のように書いてある。

(4),(8), and (9), it is clear that detection of photon s after the double slit with polarization R is compatible only with the passage of s through slit 1 and polarization L is compatible only with the passage of s through slit 2.

Double-slit quantum eraserP.033818-4

D_Pの偏光の回転方向(量子力学的にはスピン)を検出すれば、経路情報(which-path information)が得られると書いてある。 D_SとD_Pの検出結果は、量子もつれにあるので、当然、一定の相関性がある。 つまり、D_Sの偏光とD_Pの偏光には一定の相関性がある。 結果、D_Pに到達した光の偏光の回転方向(量子力学的にはスピン)を検出すれば、D_Sの偏光の回転方向が分かる。 先程の説明でスリットの前に置いたquarter-wave plateによる操作によって、双方のスリットを通過した光がいずれも円偏光であり、かつ、片方が右回転で他方が左回転となり、さらに、D_Sにどちらか一方の経路の光が届くのであれば、D_Sの偏光の回転方向は経路情報(which-path information)となる。 この前提が成立しなければ、偏光の回転方向を検出しても、経路情報(which-path information)を得ることはできない。 ただし、polarizer cube（偏光キューブ）であるPOL1を置くと、POL1を通過した光が直線偏光になってしまうので、D_Pで回転方向を検出することはできない。

しかし、恐らく、この方法で経路情報(which-path information)を得ることは不可能であろう。 その詳細は後で説明する。

POL1とQWP1とQWP2を置く 

POL1,QWP1,QWP2を全て置く場合を考える。 経路情報(which-path information)を取得する方法の記載から推測すると、おそらく、次の様になるようquarter-wave plateを配置しているのだろう。

• 垂直成分が同相の時に水平成分は逆相
• 垂直成分が逆相の時に水平成分は同相

polarizer cube（偏光キューブ）であるPOL1を通過した光は直線偏光となるが、垂直成分が取り出されるか、水平成分が取り出されるかはPOL1の向きによって変わる。 さっきも説明した通り、D_SとD_Pの検出結果は、量子もつれ状態にあるので、当然、一定の相関性がある。 結果、 D_Pに届く光も直線偏光となる。 D_Sにおいても、D_Pとどうよう、どちらの成分が取り出されるかは、POL1の向きによって変わる。

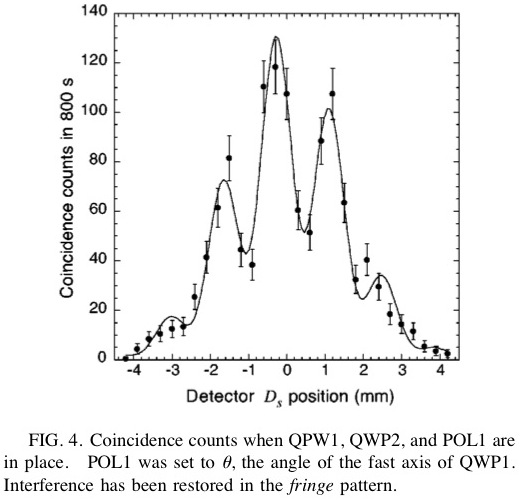
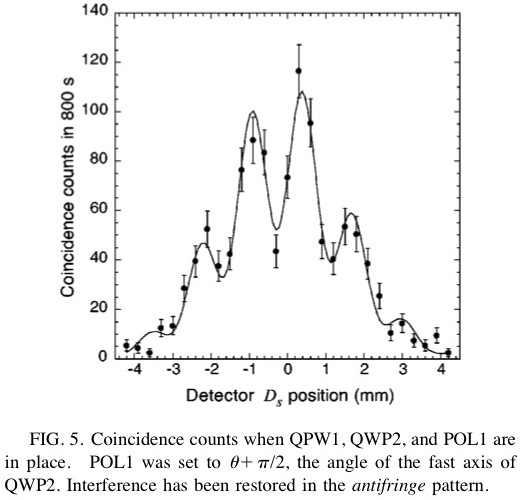
先程の位相関係を前提にすると、垂直成分と水平成分では干渉縞パターンの山と谷がそれぞれ逆となる（論文中のFIG.4とFIG.5）。

POL1なしにQWP1とQWP2を置く 

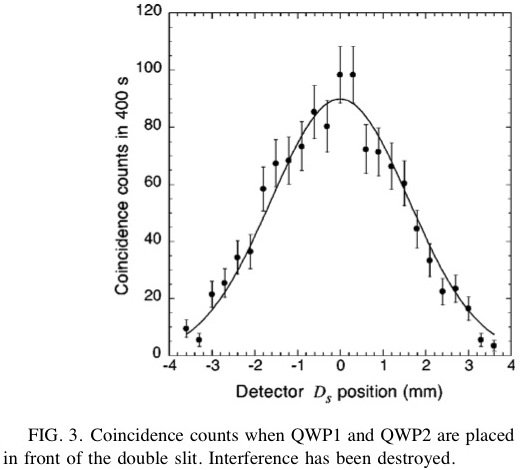
次に、POL1なしに、QWP1とQWP2を置いた状態である。 経路情報(which-path information)を取得する方法の記載から、２つのスリットを通過した光はお互いに逆回転の円偏光である。 同じ強さの２つの逆回転の円偏波(偏光)の合成は必ず直線偏波(偏光)になる。 両者の位相関係によって偏波(偏光)方向は変化するが、波の大きさ(光の強さ)には影響しない。 ２つの経路の光の干渉が光の強さに影響しなければ、光子の検出確立も変化しないので、干渉縞は生じない（論文中のFIG.3）。

垂直成分と水平成分に分けて考えても良い。 先程も説明した通り、両成分の干渉縞パターンの山と谷がそれぞれ逆となる。 よって、垂直偏波と水平偏波が同量で混ざっていれば、全体として干渉縞が消えると考えることもできる。

なお、この実験は次の２つのパターンで試して、いずれも、同じ結果が出ることが確認されている。

• D_Sより先にD_Pに光が到達するパターン
• D_Sより後にD_Pに光が到達するパターン

「coincidence counts」であるので最終的な検出結果の記録は同時に行なわれている。

実験の解説 

経路情報について 

円偏光の回転方向を検出することで経路情報(which-path information)を得ようとしているのだから、polarizer cube（偏光キューブ）であるPOL1を通して直線偏光にした後に経路情報(which-path information)が得られなくなるのは当然である。 では、POL1を置かなければ、経路情報(which-path information)を得ることは可能だろうか。

D_Sに到達する直前の波は、２つのスリットを通った波の合成波であり、それぞれが逆回転の円偏光であるので、合成波は直線偏光となる。 D_Sと相関するD_Pにも、当然、直線偏光が到達する。 直線偏光は逆回転の円偏光の合成と考えられるので、偏光の回転方向に相当するスピンを検出すると、検出結果は確率的に半々となる。 つまり、これは、スピン検出時に、直線偏光のうちの片方の回転方向の偏光成分が取り出されたと解釈される。 この検出結果が経路情報(which-path information)となるためには、検出結果が片方の経路における光のみの検出結果と一致しなければならない。 仮に、そうなるとすれば、その可能性は次の２つであろう。

• D_Pには、どちらか一方の経路の光に相関した光しか到達しない
• D_Pにて、２つの経路の光に相関した光が分離されて、そのうちの片方のみを検出する

いずれの場合であっても、検出結果が経路情報(which-path information)となるためには、D_Pと相関した一方の経路の光のみをD_Sにおいても検出することになる。 それでは、ランダムにどちらかの経路を塞いだ事実上の単一スリット実験(以下、「ランダム単一スリット実験」)になってしまう。 二重スリット実験では、射影仮説による「波束の収縮」後の可観測量は合成波によって決定される。 それに対して、ランダム単一スリット実験では一方の経路の波のみで可観測量が決定される。 両者は明らかに条件が違う。 つまり、検出結果が経路情報(which-path information)となるためには、二重スリットの前提が崩れることを必要とする。 言い換えると、二重スリットの前提が維持される場合は、検出結果が経路情報(which-path information)となる可能性は否定される。

POL1を置いた場合の結果を考慮すれば、可観測量が合成波によって決定されているように見える。 それでは、検出結果は経路情報(which-path information)にはならないだろう。 しかし、奇妙な仮定を置けば、特定の実験セットにおいてのみ検出結果が経路情報(which-path information)となると主張することは可能である。 ただし、検出結果が経路情報(which-path information)となるためには、二重スリットの前提が崩れることが必須であることには変わりがない。 二重スリットの前提を維持したまま、経路情報(which-path information)を得ることはできない。

以上、まとめると、この実験で二重スリットの前提が崩れるかどうかは定かではないが、二重スリットの前提を崩すことが干渉を阻害することは否定できない。 しかし、二重スリットの条件を維持したまま経路情報(which-path information)を得ることが可能だとは証明されていないし、仮に、可能だとしてもそれが干渉を阻害することは全く示されていない。 もしも、検出した偏光の回転方向が経路情報(which-path information)であるとするなら、それを実験で証明する必要がある。 でなければ、それは経路情報(which-path information)として意味を持たない、ただのランダムなデータに過ぎない。

いずれにせよ、従来理論に基づいた考察で説明不可能な現象は何一つ発生していない。 ちなみに、POL1の代わりに、円偏光を楕円偏光にするwave plateを置いたらどうなるのだろうか？という興味は唆られる。

干渉について 

POL1なしにQWP1とQWP2を置くと、何故、干渉縞が消えるのか。 この場合、波の干渉結果が、偏波(偏光)方向のみに影響し、波の大きさ(光の強さ)には影響しないため、干渉縞は現れない。 垂直成分と水平成分に分けて考えるなら、位相が不揃いになることによって干渉縞が平滑化されると見なしても良い。 つまり、POL1なしにQWP1とQWP2を置くだけなら、干渉そのものが発生しないわけではなく、干渉縞として現れないだけである。

POL1とQWP1とQWP2を置くことで干渉縞が復活したのは、干渉結果が波の大きさ(光の強さ)に影響するようになったからである。 垂直成分と水平成分に分けて考えるなら、混ぜ合わせた一方のみを選択的に取り出した結果、位相の不揃いを解消すると見なしても良い。

以上の通り、従来理論に基づいた考察で説明不可能な現象は何一つ発生していない。

まとめ 

以上の通り、干渉縞の有無も経路情報(which-path information)の取得可否も、どちらも従来理論に基づいた考察で十分に説明が可能である。 あたかも経路情報(which-path information)を付加しようとすると干渉縞が消えるかのようにも見えるが、たまたまそのようになったのか、あるいは、そうなる必然性があったのかは、この実験結果からは知りようがない。 よって、この実験結果から、経路情報の付加と干渉消失の因果関係を推定することは不可能である。

尚、二重スリット量子消しゴム検証実験の提唱に検証実験の具体的方法を提唱している。

簡易版？ 

ちなみに、 この実験の「簡易版」 とやらでは偏波面が直交することにより、干渉結果が波の大小に影響しなくなる。 コメント欄に書かれているように、偏光板が偏波面の直交性を生むことによって、干渉縞が消えている。 なお、そこに書かれている科学的誤りは二重スリット量子消しゴム実験トンデモ解説に移動した。

誤った説明の例 

誤った説明の事例は二重スリット量子消しゴム実験トンデモ解説に移動した。

• 「簡易版」とやらの間違い
• ニコニコ動画の間違い
• 河合塾による疑似科学紹介