デジタルFIRフィルタ係数値(結論のみ)

初めに

ここではFIRフィルタのパラメータについて結論だけ手っ取り早く示す。 ただし、結論と言っても、サンプリング周波数、カットオフ周波数等によってパラメータを変更する必要があるので、数式は必要になる。 だが、なるべく簡単にまとめたい。 尚、ここではFIRフィルタが何か？とか、その原理や理論については説明しない。 その辺が知りたい人は検索すれば沢山サイトが見つかるので、そちらを参照してもらいたい。

Excelファイル

計算が面倒な人のためにExcelファイルも用意した。

• パラメータ計算(1.2MB)

拡張子をxlsxに変更すればそのまま使える。 inputシートの色のついたセルに必要事項を入力するとoutputシートにフィルタのパラメータが出力される。 次のExcelファイルのfilterシートにフィルタのパラメータをコピペすれば周波数特性もわかる。

• 周波数特性計算(21.4MB)

パラメータ計算を高速化できたので、パラメータ計算と周波数特性の計算を一括で行えるファイルも用意した。

• パラメータ計算+周波数特性計算(22.7MB)

FIRの段数

周期2NをカットオフとするFIRフィルタを作るには最低でも2N+1段のFIRフィルタが必要となる。 例えば、48kHzでサンプリングした音声で100Hzをカットオフ周波数にすると最低でも481段必要になる。 段数を減らしたいなら、ダウンサンプリングすれば良い。

1. LPF(Up/Down兼用)適用
2. ダウンサンプリング
3. 目的のフィルタ適用
4. アップサンプリング
5. LPF(Up/Down兼用)適用

ただし、そちらの方が面倒かもしれない。

シャープカットオフなフィルタが必要な場合は段数を増やせば良い。 段数が多いほどフィルタの特性は良くなる。

無処理フィルタ

低域通過フィルタ(Low Pass Filter)を元に他のフィルタのパラメータを求める際に必要になるので説明しておく。 Kが-N〜Nの整数のとき、フィルタのパラメータは次のとおりとなる。

• F_k=sinc(2πK)

F₀=1で、それ以外は全て0となる。

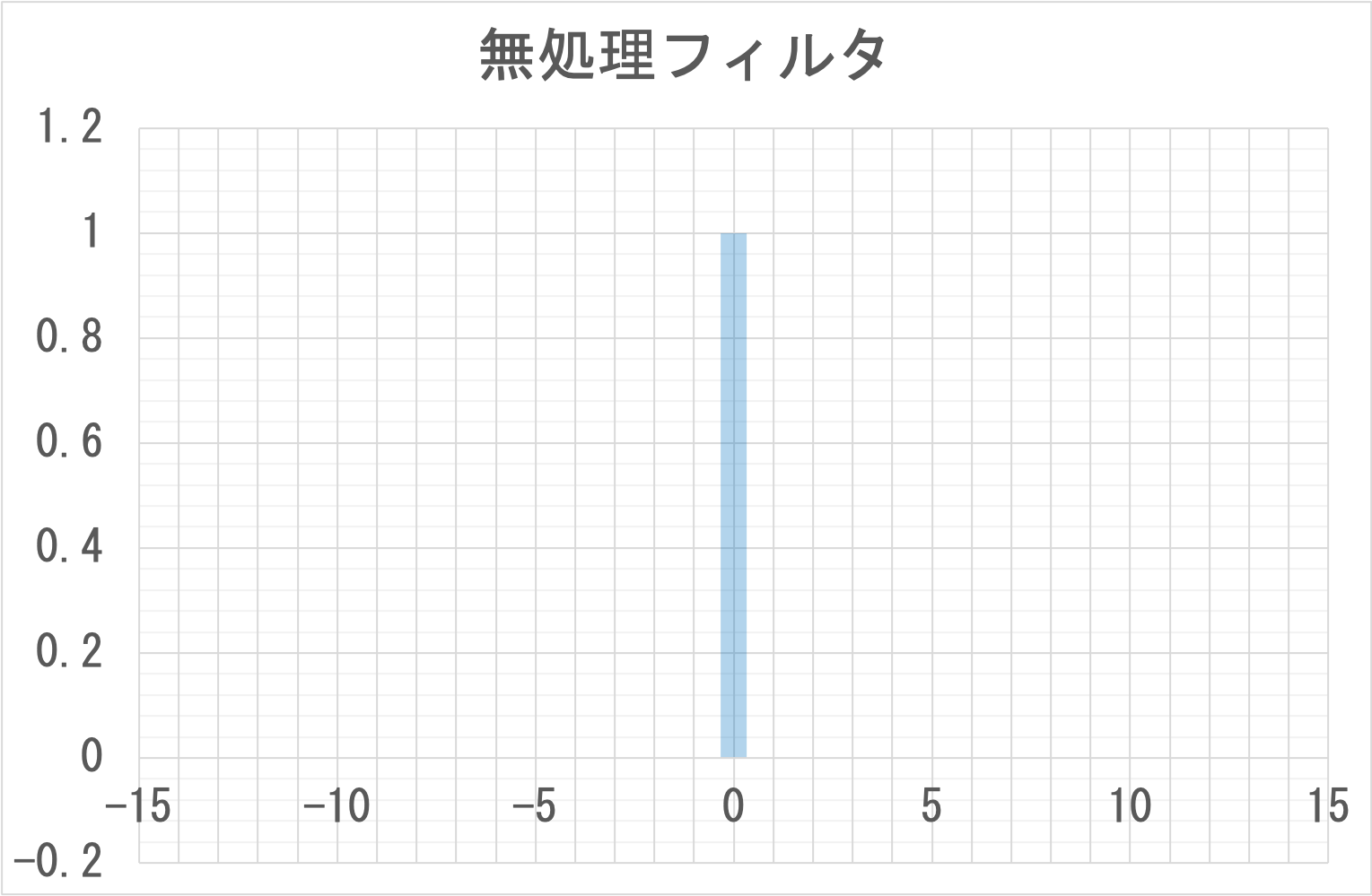
低域通過フィルタ(Low Pass Filter)

Kが-N〜Nの整数、カットオフ周期がＴ(単位：サンプル数)のとき、フィルタのパラメータは次のとおりとなる。

• F_k=(2/T)*sinc(2πK/T)

ただし、これは無限段かつ窓関数なしの場合の値となる。 例によって、窓関数が何かはここでは説明しない。 窓関数を適用した場合とそうでない場合の周波数特性を以下に示す。

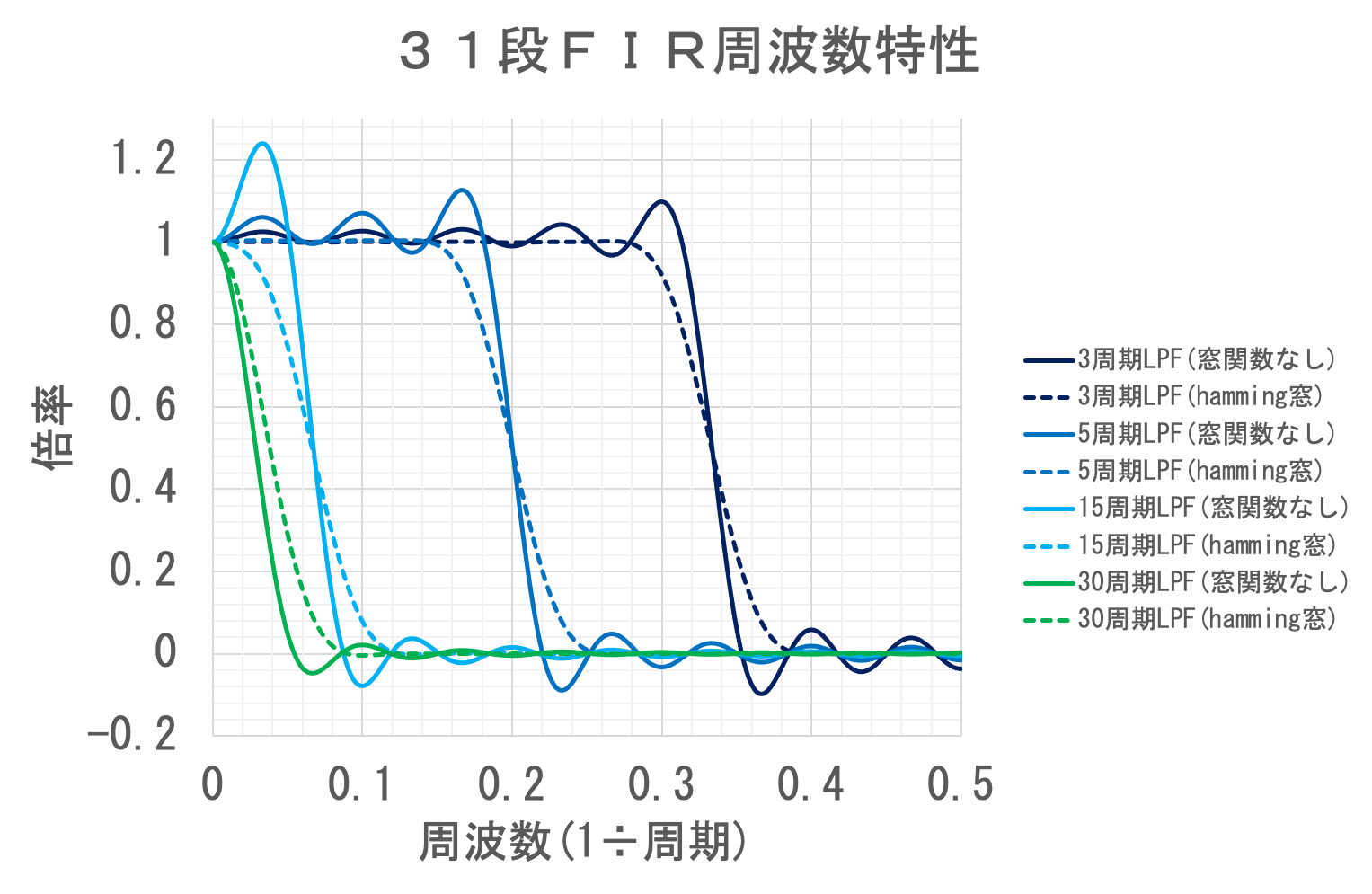
周期2Nをカットオフとする場合は特に窓関数を適用しなくても実用的にはそれほど問題にはならないかもしれない。 しかし、周期Nの場合は窓関数を適用しないと低域が大きくなりすぎる。

有限段または窓関数ありの場合は、ＧＡＩＮを１とするためには正規化が必要となる。 低域通過フィルタでは、直流(定数)成分の入力と出力が１対１になればよいので、各パラメータを全パラメータの合計で割れば良い。 尚、窓関数を適用する場合は、窓関数を適用してから正規化処理を行う。

３１段のカットオフ５周期、ハミング窓の低域通過フィルタ(Low Pass Filter)のパラメータは次のとおりとなる。

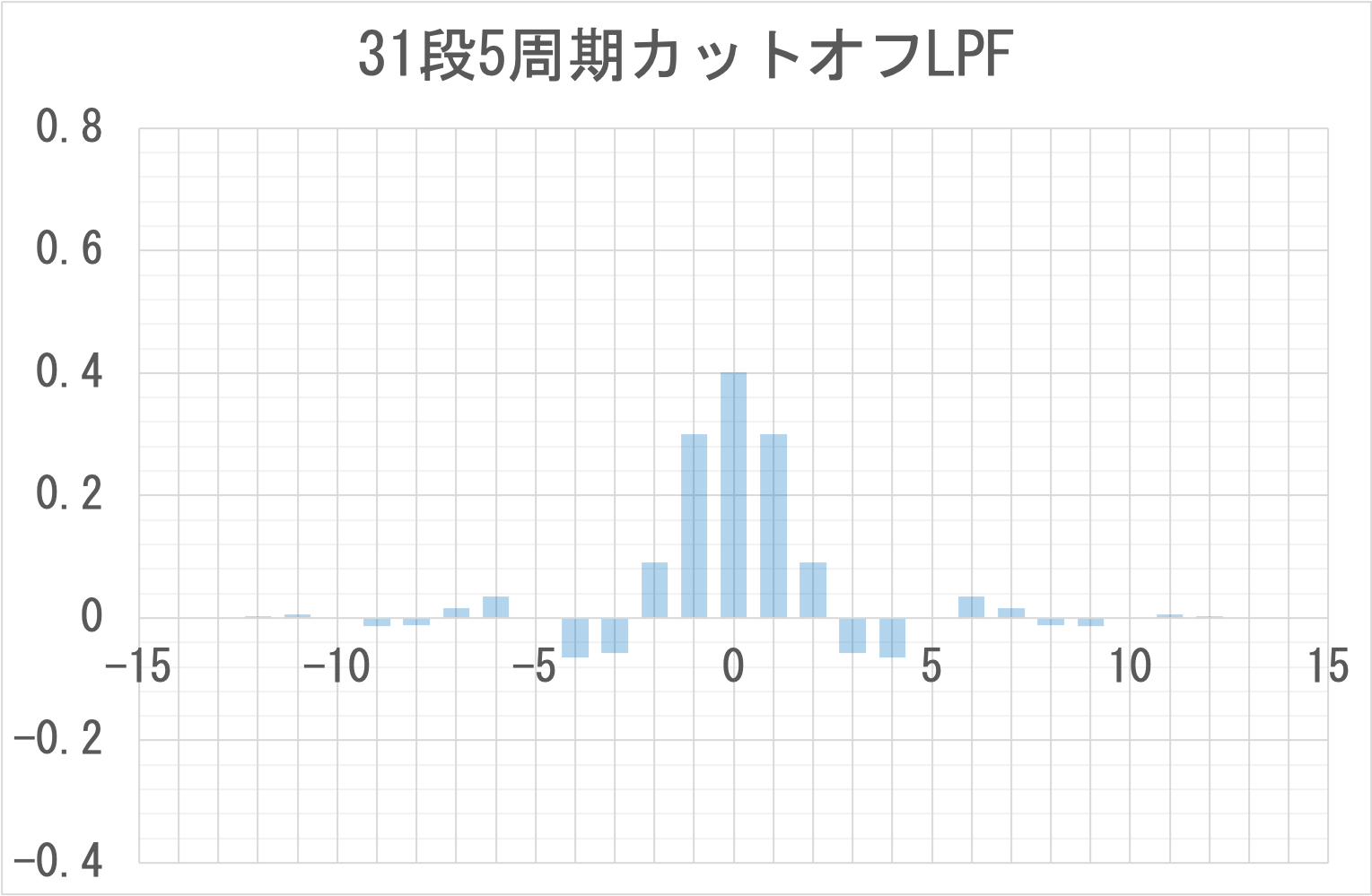
高域通過フィルタ(High Pass Filter)

Kが-N〜Nの整数、カットオフ周期がＴ(単位：サンプル数)のとき、フィルタのパラメータは次のとおりとなる。

• F_k=sinc(2πK)-(2/T)*sinc(2πK/T)

これも低域通過フィルタ(Low Pass Filter)と同様、無限段かつ窓関数なしの場合の値となる。 この式の第１項は無処理フィルタであり、第２項は低域通過フィルタ(Low Pass Filter)である。 つまり、無処理フィルタから低域通過フィルタ(Low Pass Filter)を引けば高域通過フィルタ(High Pass Filter)となる。

実際のパラメータは、各パラメータごとに無処理フィルタの値から正規化された低域通過フィルタ(Low Pass Filter)の値を引けば良い。

窓関数を適用した場合とそうでない場合の周波数特性を以下に示す。

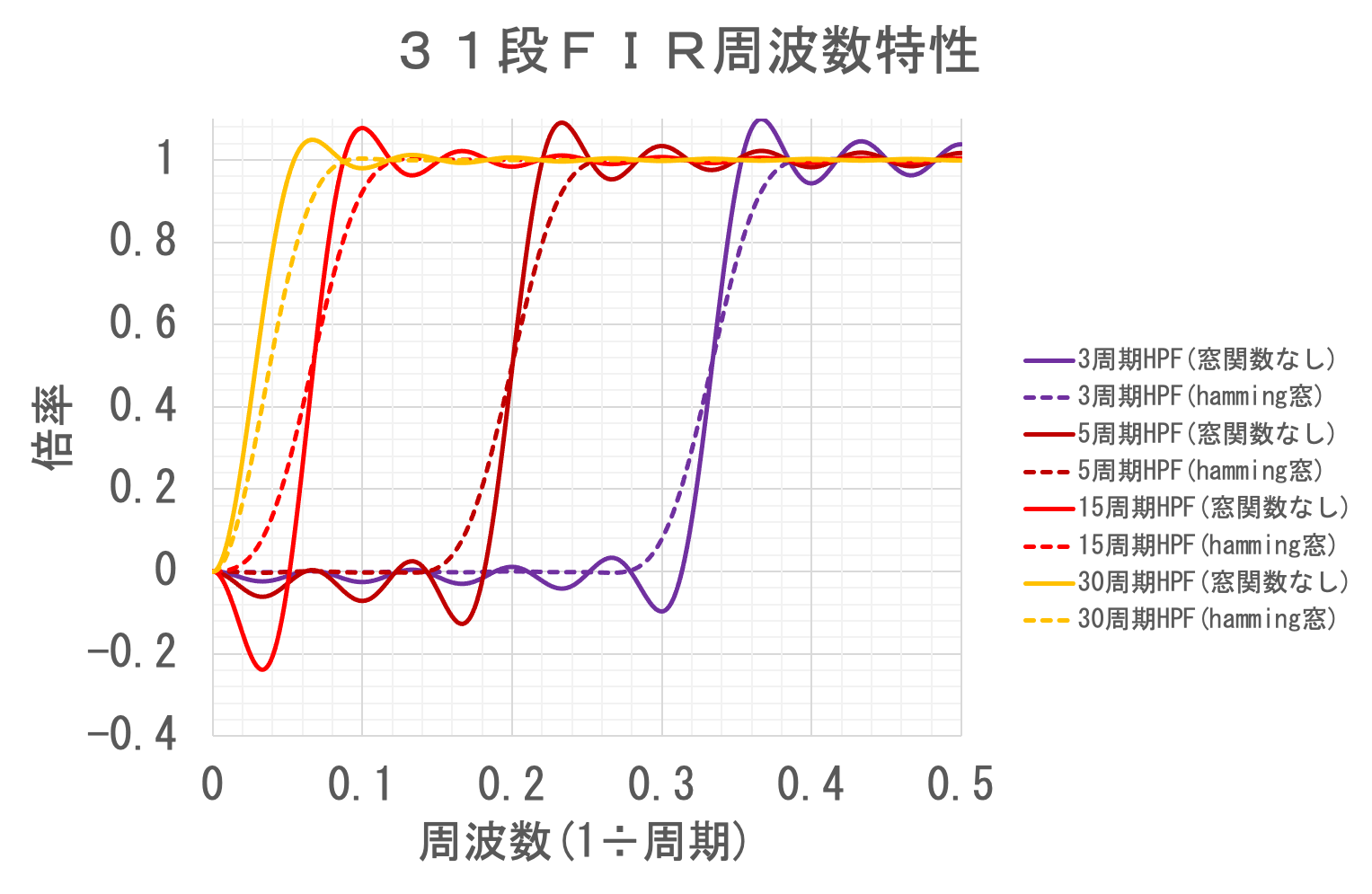
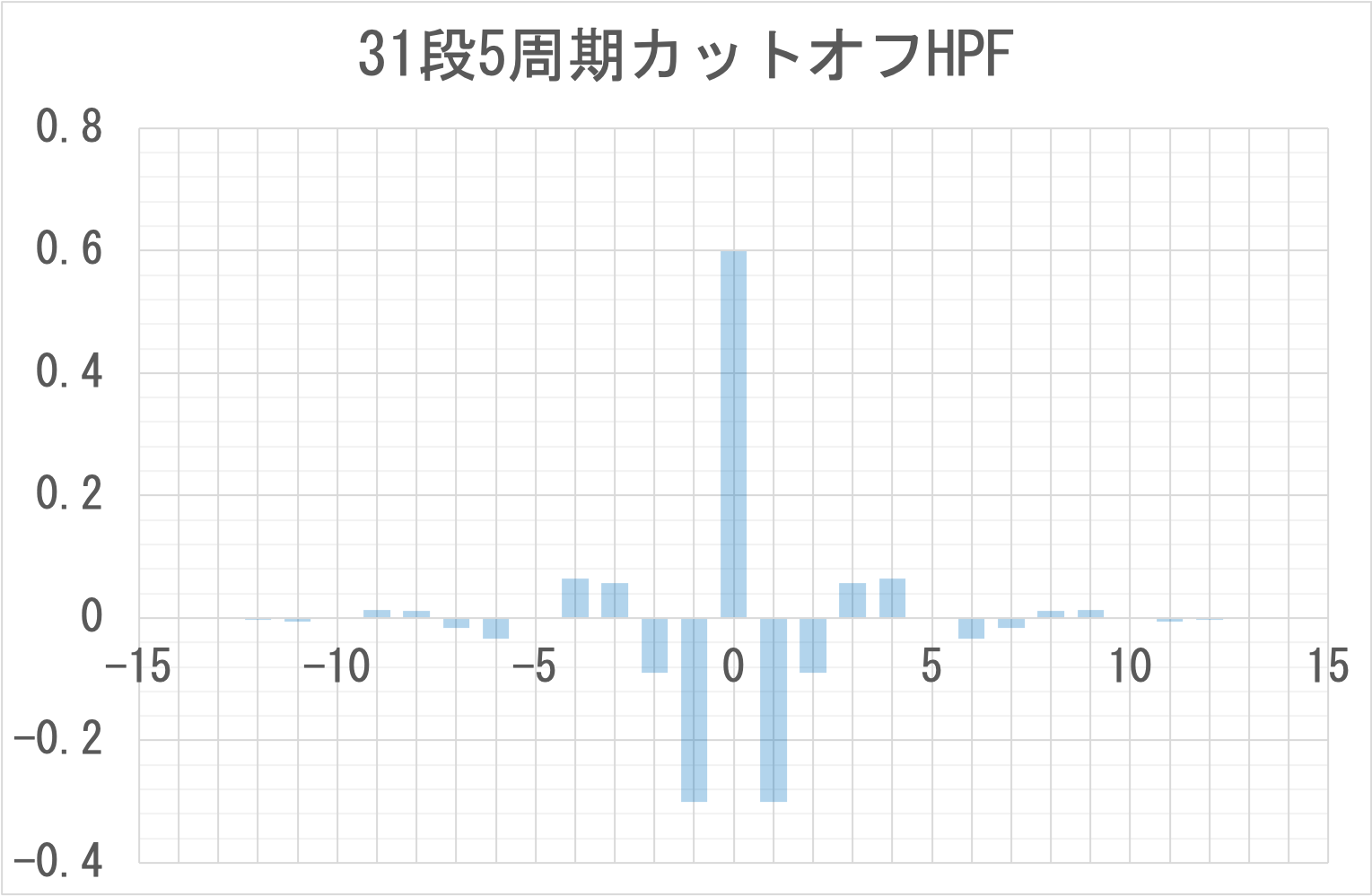
３１段のカットオフ５周期、ハミング窓の高域通過フィルタ(High Pass Filter)のパラメータは次のとおりとなる。

帯域通過フィルタ(Band Pass Filter)

Kが-N〜Nの整数、カットオフ周期がT_LおよびT_H(単位：サンプル数)のとき、フィルタのパラメータは次のとおりとなる。

• F_k=(2/T_H)*sinc(2πK/T_H)-(2/T_L)*sinc(2πK/T_L)

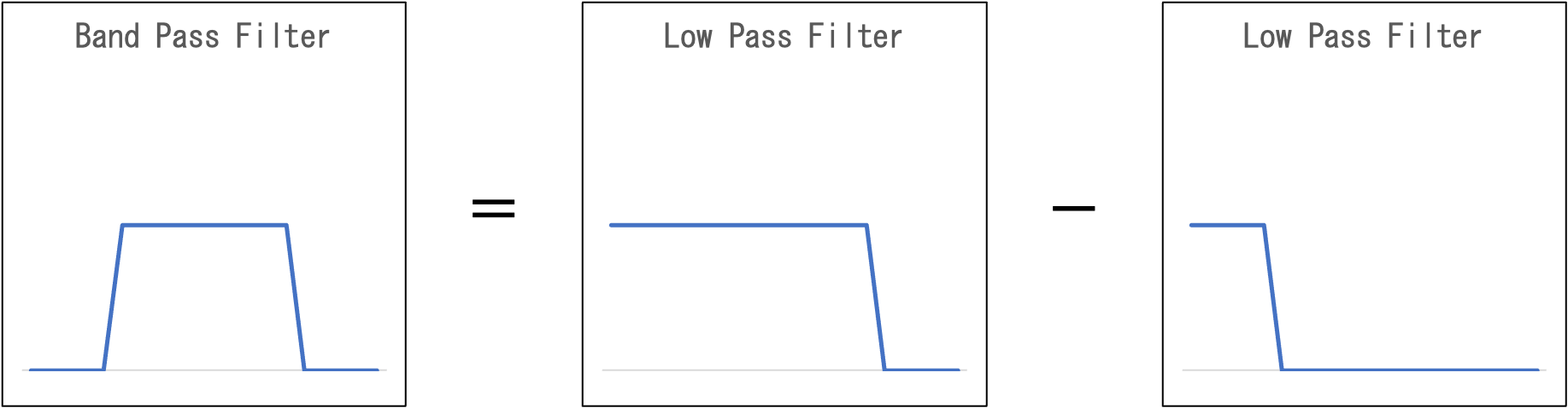
これも、例によって、無限段かつ窓関数なしの場合の値となる。 この式の第１項も第２項も低域通過フィルタ(Low Pass Filter)である。 つまり、T_Hの低域通過フィルタ(Low Pass Filter)からT_Lの低域通過フィルタ(Low Pass Filter)を引けば帯域通過フィルタ(Band Pass Filter)となる。

実際のパラメータは、各パラメータごとに正規化されたT_Hの低域通過フィルタ(Low Pass Filter)の値から正規化されたT_Lの低域通過フィルタ(Low Pass Filter)の値を引けば良い。

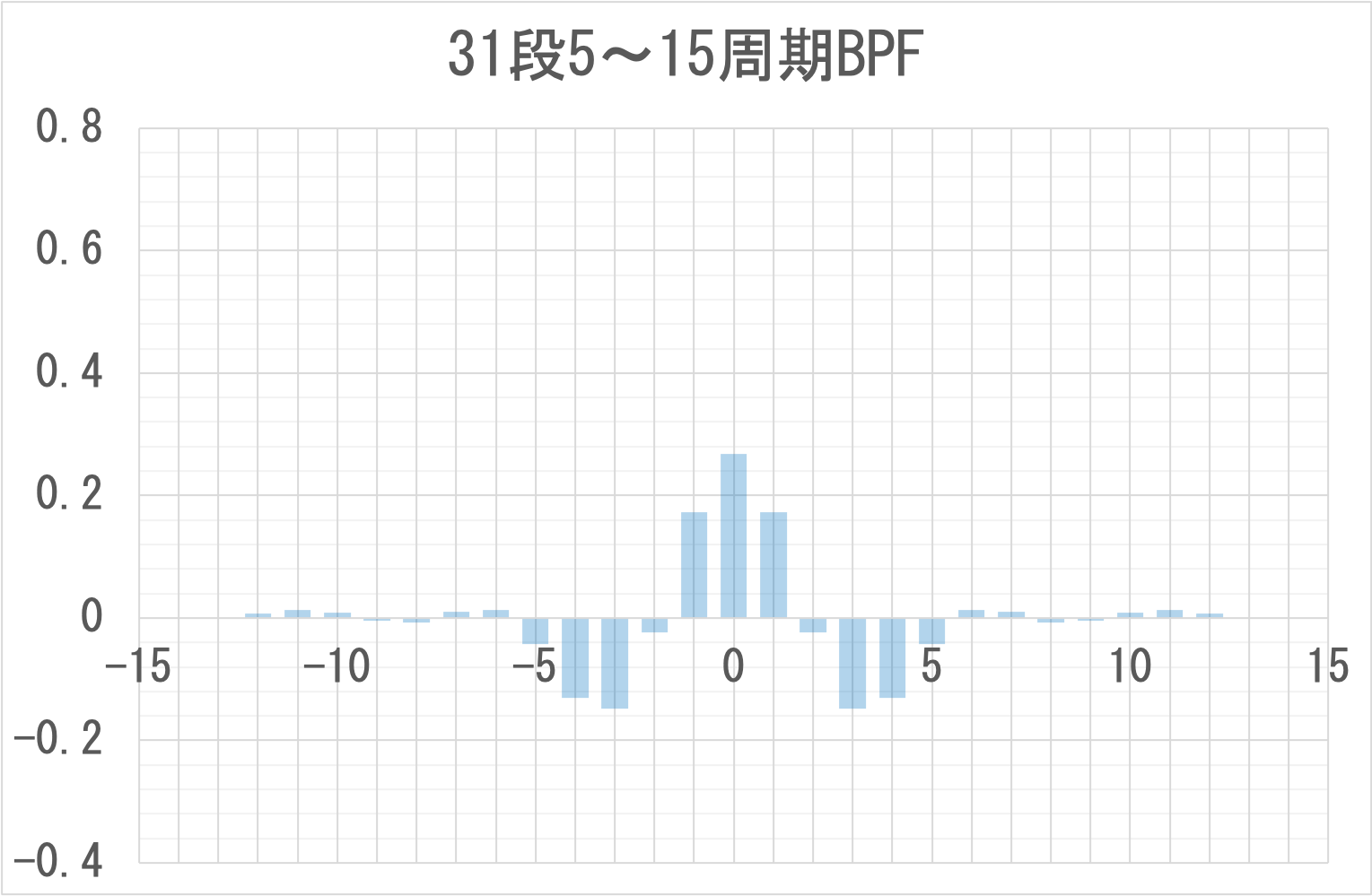
３１段のカットオフ５周期および１５周期、ハミング窓の帯域通過フィルタ(Band Pass Filter)のパラメータは次のとおりとなる。

帯域除去フィルタ(Band Elimination Filter)

Kが-N〜Nの整数、カットオフ周期がT_LおよびT_H(単位：サンプル数)のとき、フィルタのパラメータは次のとおりとなる。

• F_k=sinc(2πK)+(2/T_L)*sinc(2πK/T_L)-(2/T_H)*sinc(2πK/T_H)

これも、例によって、無限段かつ窓関数なしの場合の値となる。 この式の第１項は無処理フィルタで第２項と第３項は低域通過フィルタ(Low Pass Filter)である。 つまり、無処理フィルタにT_Lの低域通過フィルタ(Low Pass Filter)を足し、T_Hの低域通過フィルタ(Low Pass Filter)を引けば帯域通過フィルタ(Band Pass Filter)となる。

実際のパラメータは、各パラメータごとに無処理フィルタの値に正規化されたT_Lの低域通過フィルタ(Low Pass Filter)の値を足し、そこからさらに正規化されたT_Hの低域通過フィルタ(Low Pass Filter)の値を引けば良い。

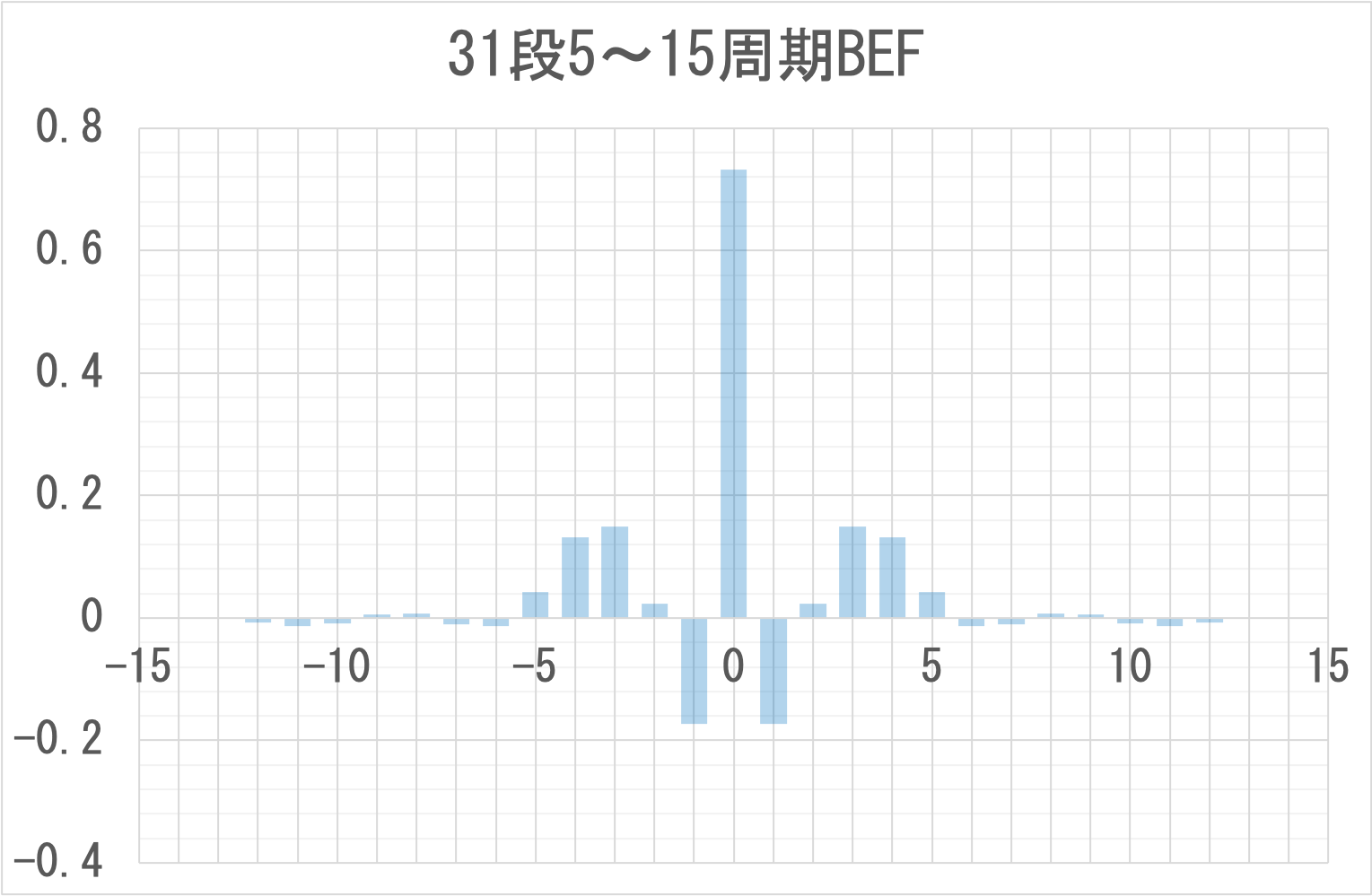
３１段のカットオフ５周期および１５周期、ハミング窓の帯域除去フィルタ(Band Elimination Filter)のパラメータは次のとおりとなる。