遅延選択量子消しゴム実験

• 前置き
  • 科学で扱える現象の範囲
  • 相関からの考察
  • オッカムの剃刀
• 概要
• 実験内容
• まとめ
• 空想
• 誤った説明の例
• 参考

前置き 

手っ取り早く結果を知りたい方は以下にどうぞ。

• 本当の量子消しゴム実験 - YouTube
• 量子消しゴム実験は実は何も消していない - Togetter
• 量子消しゴム実験まとめ

当サイトの科学項目の目的も参照のこと。

科学で扱える現象の範囲 

科学で扱うためには、同じ条件では同じ現象になる(同じ数式で記述できる)ことが必須の前提となる。 その前提が崩れれば、科学法則が成立しないし、実験の再現性も失われる。 よって、科学法則を見出したり、実験で結果を確かめるためには、この前提が崩れてはならない。 言い換えると、同じ現象にならない(同じ数式で記述できない)ケースを科学で扱うためには両者には違う条件が必要となる。 尚、量子力学は確率的に結果を推定する理論であるので、ここで言う「現象」には確率も含む。

相関からの考察 

AとBに相関が見られる時に考えられる可能性は4つある。

• Aが原因でBが結果
• Bが原因でAが結果
• C(統計学では「交絡因子」と呼ばれる)が原因でAもBも結果
• 単なる偶然

ただし、実験の再現性が極めて高ければ、４番目の可能性は否定される。 ネット上の考察の多くの問題は３番目の可能性、すなわち、交絡を考慮していない点にある。 交絡を考慮すれば、実験結果は、交絡因子が原因だと示唆していること、そして、AとBの相関を直接的な因果関係と考えることが困難なことが理解できよう。

オッカムの剃刀 

実験結果を説明するために不要な仮定は置かない。 必要のない仮定を置いても、理論的考察の役にたたない。 無駄に話を難しくすれば、間違いを生みやすくなる。 メリットが全くなく、かつ、デメリットしかない不要な仮定は可能な限り排除すべきだろう。

概要 

ここでは二重スリット量子消しゴム実験とは別の方法の量子消しゴム実験を紹介する。 勘違いしないよう要点を以下にまとめる。

• BBOで初期位相がランダムに乱される(両経路の位相乱れ量は独立変数)ため、経路測定してもしなくても干渉縞は見えなくなる
• 初期位相差の確率的情報(位相補正情報)に応じて結果を抽出すると干渉縞が見えるようになる
• 経路測定と位相測定(位相補正情報の測定)は、どちらか一方しか選択できない(経路情報と干渉縞はどちらか一方しか選択できない)
  • 経路測定すると干渉縞復活に必要な位相補正情報が手に入らない
  • 干渉縞復活に必要な位相補正情報を手に入れると経路測定できない

もう少しシンプルに説明すると次のようになる。

	経路測定なし	経路測定あり
位相測定結果に伴う抽出なし	干渉縞消失	干渉縞消失
位相測定結果に伴う抽出あり	干渉縞復活	(未確認)

• 干渉縞が復活する場合は、経路測定の準備はしているが、経路測定はしていない(経路測定しないことは干渉縞復活の必要条件である)
• 経路測定しなくても位相測定(位相補正情報の測定)しなければ干渉縞は復活しない(経路測定しないことは干渉縞復活の十分条件ではない)

ようするに、干渉縞を左右しているのは、経路測定の有無ではなく、位相測定の有無である。

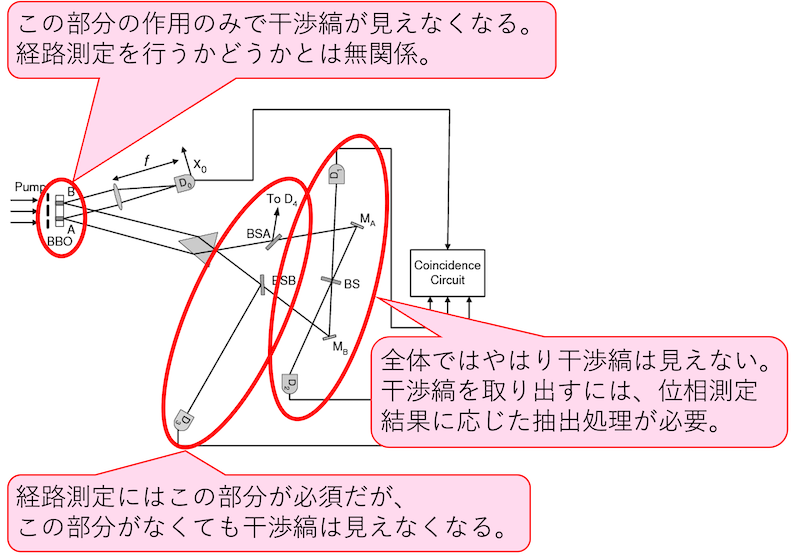
この実験の現象は全て古典力学の範囲で説明可能である。 にも関わらず、この実験の現象が不可思議に思えるのは、次の２つを混同した説明に騙されているだけである。

• 干渉縞の発生
• 干渉の発生

干渉縞が発生すれば干渉が発生していないことはあり得ないが、干渉が発生しても干渉縞が発生しないことは珍しくない。 この実験は、まさに、その干渉が発生しても干渉縞が発生しない状況を作り出すものである。 そのことを念頭に置いていれば、この実験における現象は全て古典力学の範囲で説明可能である。 尚、量子もつれの全貌は古典力学では説明できない。 しかし、本実験の結果を説明するために必要な性質(ペア間の初期位相の同期)だけに限れば古典力学の範囲で十分に説明可能である。

量子消しゴム(quantum eraser)とは、非常に誤解を招く言い回しである。 事実、ネット上には「経路情報(which path information)を後から消せば、干渉縞が復活する」という実験事実に反した言説が多く見られる。 この実験で消しているものは、どちらのスリットを通過したかの情報＝経路情報(which path information)ではなく、強いて言えば、それを測定する機会である。 経路情報(which path information)を測定しなくても、測定可能な実験セットにするだけで、干渉縞が消失する。 そして、この実験における経路印(which path marker)からは、経路情報(which path information)か干渉縞を復活させるための情報のいずれかを入手できる。 そして、どちらか一方を手に入れると他方は手に入らないし、一度手に入れた情報を他方に変換することもできない。 経路情報(which path information)を手に入れることは干渉縞を復活させるための情報を手に入れる機会を放棄することであり、干渉縞を復活させるための情報を手に入れることは経路情報(which path information)を手に入れる機会を放棄することである。 つまり、経路情報(which path information)を測定しない場合に限って、干渉縞を復活させることが可能になるのである。 経路情報(which path information)を測定してしまうと、既に干渉縞を復活させるための情報の入手機会が失われているため、後からどうやろうとも、経路情報(which path information)を消去しようとも、干渉縞を復活させることはできない。

干渉縞が消失する場合について「波動性が消失する」と説明されることがあるが、これも間違っている。 この実験で確認されたことは干渉縞の消失であって波動性の消失ではない。 そして、この実験結果は、波動性を維持したままで説明可能な現象である。 というか、波動性がある場合と条件が同じなのに波動性がなくなると考える理由がない。 波動性の有無についての検証は一切行われておらず、波動性が消失した証拠は一切ない。

まとめると、この実験結果は、干渉縞の成立要件を乱す物理的作用を伴う物理的細工(交絡因子C)が原因と考えれば、経路測定(A)も干渉縞の消失(B)もその結果として説明できる。 そして、そのような物理的細工を施した場合は、経路測定しなくても干渉縞が消失するため、経路測定が干渉縞の消失の原因と考えることは困難となる。 また、干渉縞が消失する場合にも、相殺された隠れた干渉縞の存在を示唆する実験結果が出ている。 確かに、相殺された隠れた干渉縞を抽出するためには、位相測定結果が必要となるが、それは、位相測定と経路測定が両立しないからである。 それは、1つの光子に対しては、位相測定か経路測定のどちらかしかできないせいである。 と言うと、経路測定した場合に隠れた干渉縞の存在を確認していない点を指摘する者がいるかも知れない。 しかし、最初に説明した科学で扱う必須の前提「同じ条件では同じ現象になる(同じ数式で記述できる)」が成立するならば、位相測定した場合と経路測定した場合で図の上側の結果は同じであると推定できる。 何故なら、上側における条件の差を示唆する根拠が何もないからである。

• 条件の差を仮定する必然性がない(下側における物理的操作が上側の結果に影響を与えなくても実験結果は何の不都合もなく説明できる)
• 実際に結果は変わっていない(経路測定してもしなくても干渉縞は消失する)

よって、経路測定した場合にも隠れた干渉縞が存在すると推定できる。

実験内容 

原論文の草案は A Delayed Choice Quantum Eraser - arXiv.org である。 尚、査読を受けて専門誌に掲載された版はDelayed “Choice” Quantum Eraser (Physical Review Letters)である。

In 1982, Scully and Drü̈hl found a way around this position-momentum uncertainty obstacle and proposed a quantum eraser to obtain which-path or particle-like information without scattering or otherwise introducing large uncontrolled phase factors to disturb the interference. To be sure the interference pattern disappears when which-path information is obtained. But it reappears when we erase (quantum erasure) the which-path information [3,4]. Since 1982, quan- tum eraser behavior has been reported in several experi- ments [5]; however, the original scheme has not been fully demonstrated.

1982年にScullyとDrühlは、この位置 - 運動量の不確定性を回避する方法を見つけ、干渉を妨害する散乱や制御されていない大きな位相要因を導入することなく、経路または粒子状情報を得るための量子消去を提案した。 経路情報を取得したときに干渉パターンが確実に消えるようにする。 しかし、経路情報を消去（量子消去）すると、それが再び現れる[3,4]。 1982年以来、いくつかの実験で量子量子消去の挙動が報告されているが [5]、元の方式は完全には実証されていない。

---

In conclusion, we have realized a quantum eraser experiment of the type proposed in ref. [3].

結論として、我々は参考文献[3]で提案されたタイプの量子消去実験を実現した。

A Delayed Choice Quantum Eraser - arXiv.org

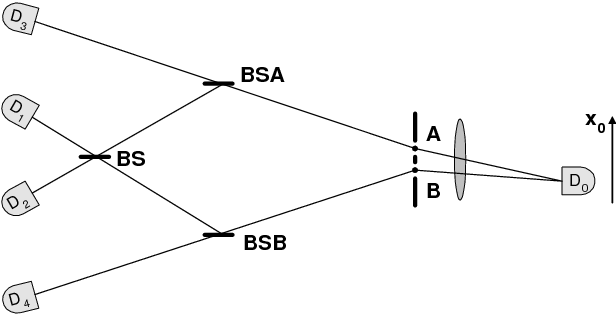
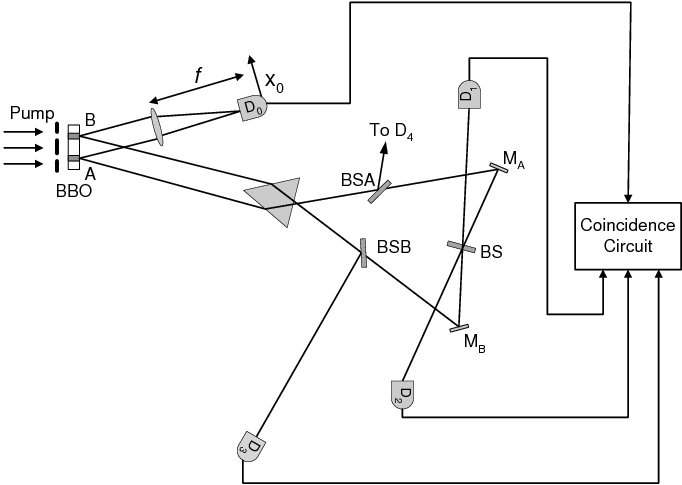
Delayed "Choice" quantum eraser - SemanticScholar

この実験におけるBSAやBSBは、本来、人為的にミラーを置くか何も置かないかを選択するものである。 Delayed Choice (遅延選択)である以上、厳密には、そうでなければならない。 しかし、この実験では、ハーフミラーに置き換えて、選択を自然の現象に委ねている。 それにより、厳密さを欠くが、実験の手間を減らすことができる。 この実験の趣旨を鑑みれば、厳密なDelayed Choice (遅延選択)である必要性は乏しいので、それでも問題はないと考えられる。

FIG. 1(上側の図)とFIG. 2(下側の図)では逆になっているので、以下は、FIG. 2で説明する。 type-Ⅱ phase matching nonlinear optical crystal BBO (第二種位相整合非線形光学結晶メタホウ酸バリウム)では、入射光の２倍の波長の量子もつれした２つの方向に進む光に分離される。 入射光が光子１個分なら、放射光はそれぞれ光子１個分で合計光子２個分となる。 その際、２つの放射光の間の位相は同期関係となるが、入射光の位相とは全く無関係となる。 その様子を以下に示す。

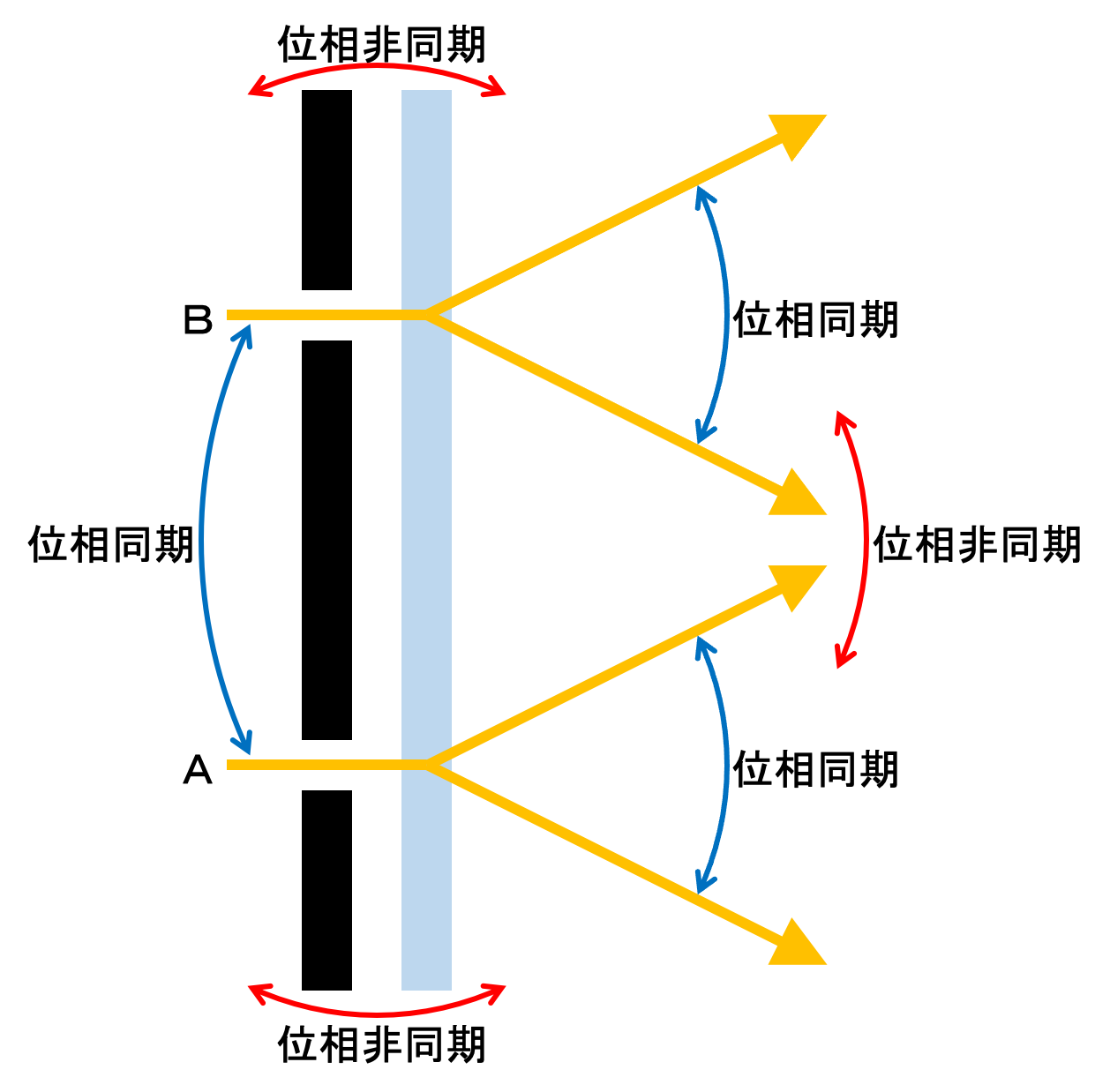
BBOから放射される光のうち、上方向に向かう光は２つとも同方向に向かっており、最終的にD₀で検出される。 D₀はX方向に移動可能で、ゆっくりと移動させながら光子を検出する。 光子１個分相当の光を用いて、何万回も実験を繰り返し、X座標と光子の検出数の関係をグラフ化すれば、これは正しく二重スリット実験を数値化したものとなる。

BBOから放射される光のうち、下方向に向かう光は、それぞれ、BSAとBSBに到達する。 BSAやBSBはハーフミラーであり、それぞれ、半分反射して、かつ、半分透過させる。 BSAで反射した光はD₄に到達し、BSBで反射した光はD₃に到達する。 二重スリットで２つに分かれる前の光が１つの光に相当する場合、D₃とD₄に到達する光は、それぞれ、光子４分の１個分となる。 よって、これらで光子を検出する確率はそれぞれ２５％となる。 D₃に到達する光はスリットBを通過した光であり、D₄に到達する光はスリットAを通過した光である。 BSAやBSBに向かう光子とD₀に向かう光子は量子もつれの関係にあり、もしも、量子もつれの双方の通過スリットの検出結果が一致するならば次の関係が成立する。

• D₃で光子を検出したなら、この光子はスリットBを通過しているから、D₀で検出した光子もスリットBを通過している
• D₄で光子を検出したなら、この光子はスリットAを通過しているから、D₀で検出した光子もスリットAを通過している

よって、D₃とD₄の検出結果は二重スリット実験における光子の通過スリットを示している。 ただし、本当に量子もつれの双方の通過スリットの検出結果が一致するかどうかは後述する方法での検証が必要である。

一方で、BSAとBSBを透過した光は、ハーフミラーBSを通して、D₁で同相合成、D₂で逆相合成される。 もしも、BBOの入射光と放射光の位相が同期していれば、D₁では強め合い、D₂では弱め合う。 結果、二重スリットで２つに分かれる前の光が１つの光に相当する場合、D₁に到達する光は光子２分の１個分、D₂に到達する光は光子０個分となる。 よって、これらで光子を検出する確率はそれぞれ５０％と０％となる。 実際の所、BBOの入射光と放射光の位相は全く無関係となるため、検出確率は０％〜５０％となる。 ここで、スリットＡ側で位相がφ_Aだけシフトし、かつ、スリットＢ側で位相がφ_Bだけシフトするものとし、Δφ＝φ_A-φ_Bと置く。 各検出器の検出確率とΔφの関係は次のグラフとなる。

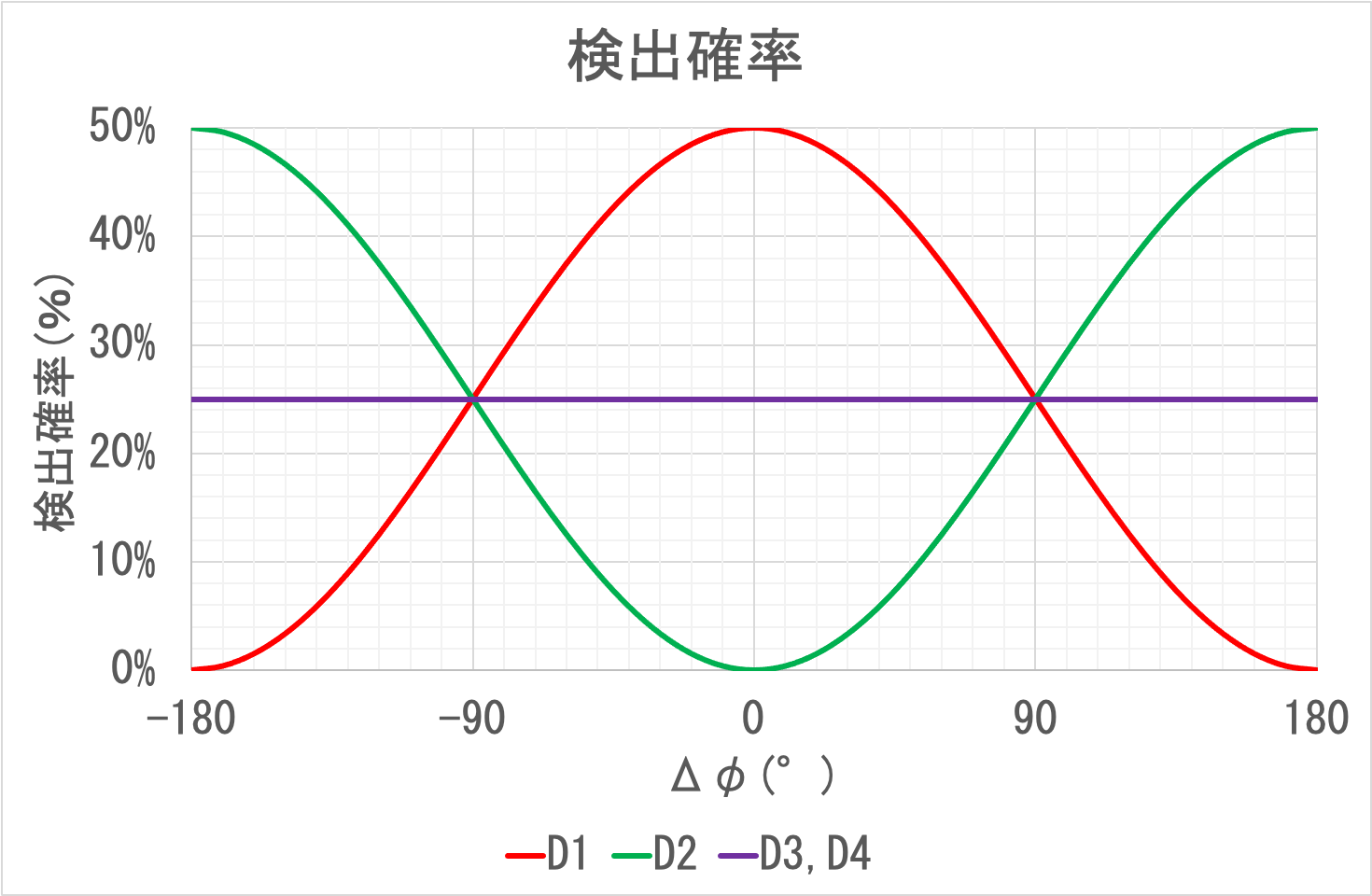
D₃の検出確率はΔφが０°に近いほど大きくなり、D₄の検出確率はΔφが180°に近いほど大きくなる。 よって、D₃とD₄の検出結果は、Δφの値を大雑把に推定する情報となる。

ここで、D₀のうち、Dⱼ(j=1,2,3,4)と相関する(ほぼ同時に検出した)結果のみを抽出したものをR₀ⱼとする。 光源から検出器に光が届くまでの時間において１個分相当以下の光子にしかならない様に光源の強度を弱めれば、偶然に全く無関係の光子をほぼ同時に検出する確率は極めて低いから、ほぼ同時に検出することをもって高確率で量子もつれのペア同士であると推定できる。 これらは、先ほどの説明から次のようになっている。

R₀₁+R₀₂

経路測定しない場合のD₀の検出結果

R₀₁

経路測定しない場合で、かつ、Δφが０°に近い場合のD₀の検出結果

R₀₂

経路測定しない場合で、かつ、Δφが180°に近い場合のD₀の検出結果

R₀₃+R₀₄

経路測定する場合のD₀の検出結果

R₀₃

経路測定する場合で、かつ、経路Bを通過した場合のD₀の検出結果

R₀₄

経路測定する場合で、かつ、経路Aを通過した場合のD₀の検出結果

R₀₁やR₀₂は、経路測定しない場合の結果ではなく、さらに、そこからΔφ別の抽出を行った結果である。 経路測定しない場合の結果は、R₀₁+R₀₂である。 同様のことはR₀₃とR₀₄にも言える。 そのことを正しく理解していないと結果の解釈を誤ってしまう。

さて、R₀₁+R₀₂、R₀₃+R₀₄のどちらにも干渉縞は見られない。

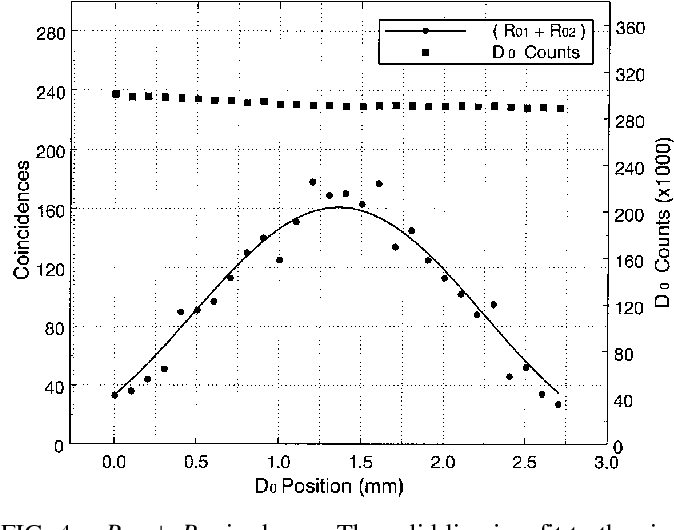
Delayed "Choice" quantum eraser - SemanticScholar

確率分布をイメージに直すと次のようになる。

ところが、R₀₁とR₀₂を分離すると、それぞれに、逆パターンの干渉縞が現れる。

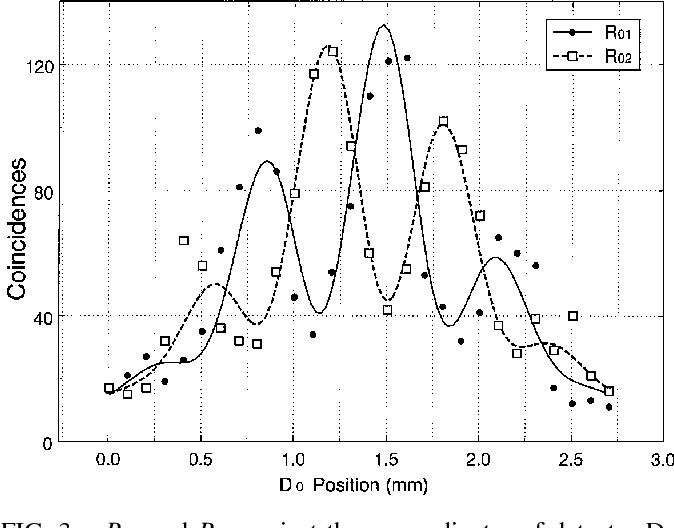
Delayed "Choice" quantum eraser - SemanticScholar

確率分布をイメージに直すと次のようになる。

先ほどの説明を踏まえると、R₀₁はΔφが０°に近いデータであり、R₀₂はΔφが180°に近いデータである。 完全に０°のデータや180°のデータのみを抽出しているわけではないので、干渉縞が少しぼやける(グラフの谷の部分がゼロにならない)。 ここで、R₀₁を赤にR₀₂を緑に色分けすると次のようになる。

これを見ると分かる通り、全体では干渉縞が見えなくても、そこに２つの干渉縞が隠されていることが分かる。 ここから干渉縞を取り出すためには、R₀₁(赤)またはR₀₂(緑)のみを選んで取り出せば良い。 実際に、R₀₁(赤)のみを選んで取り出すと次のようになる。

同様に、R₀₂(緑)のみを選んで取り出すと次のようになる。

以上の通り、R₀₁とR₀₂を分離することで２つの干渉縞が取り出せた。

R₀₃+R₀₄も確率分布ではR₀₁+R₀₂と同じであり、結果には両者の差異は見られない。 また、後で説明する通り、実験には両者に差異を生じさせるような要因も存在しない。 よって、通常の常識で類推すれば、やはり、お互いに逆パターンとなるΔφが０°に近い干渉縞とΔφが180°に近い干渉縞が相殺しあっていると考えられる。 一方で、R₀₃+R₀₄については、Δφを検出することができないので、相殺された干渉縞の分離操作を行うことはできない。

論文では干渉縞の確率分布はそれぞれ次のような式で表されている。

• R₀₁の確率分布(FIG. 3) ∝ sinc²(xπa/λf) cos²(xπd/λf)
• R₀₂の確率分布(FIG. 4) ∝ sinc²(xπa/λf) sin²(xπd/λf)

sinc(x)

sin(x)÷x

このうち、sinc関数で表されている部分が、スリットを通過した光の指向特性であり、sinとcosで表されてる部分が両経路による干渉の結果である。

以下の図は、ちゃんと、R₀₁とR₀₂をそれぞれの確率分布に従ってシミュレーションしている。

この図は、どちらも同じ色で点描しているため、見た目ではR₀₁とR₀₂を区別できない。 次の図は、同じ図をR₀₁とR₀₂で色分けしたものである。

このように、経路情報を断念した場合の全データは、干渉縞が全く見えない。 すなわち、経路情報を断念しただけでは干渉縞が復活しないことが分かる。 結果を表にまとめると良くわかるだろう。

	経路測定なし	経路測定あり
位相測定結果に伴う抽出なし	干渉縞消失	干渉縞消失
位相測定結果に伴う抽出あり	干渉縞復活	(未確認)

表を見れば、干渉縞を復活させた原因が、経路測定の断念ではなく、位相測定結果に伴う抽出操作であることが一目瞭然である。 以下、三角関数を用いた確率計算を行うが、計算が苦手な人は読み飛ばしてもらいたい。

---

ここで、量子もつれのペア間の初期位相差が常に定数(必ずしも０である必要はない)となるものと仮定する。 計算を簡単にするために量子もつれのペア間の初期位相差が０の場合を計算することとし、経路Ａ側(原論文に記載)で位相がφ_Aだけシフトし、かつ、経路Ｂ側で位相がφ_Bだけシフトするものとし、Δφ＝φ_A-φ_Bと置く。 また、説明の便宜上、D₃、D₄側の経路を無視する(Fig.1ではBSA/BSBが全反射鏡、Fig.2ではBSA/BSBに何も置かない)。 その場合、D₁の波の振幅は|cos(Δφ/2)|に比例し、D₂の波の振幅は|sin(Δφ/2)|に比例する。 波の振幅の自乗が存在確率に比例するので、D₁の検出確率はcos²(Δφ/2)＝{1+cos(Δφ)}/2、D₂の検出確率はsin²(Δφ/2)＝{1-cos(Δφ)}/2となる。 つまり、Δφが０°に近いほどD₁で検出される確率が高くなり、Δφが180°に近いほどD₂で検出される確率が高くなる。 よって、R₀₁を抽出することはΔφが０°に近い結果を高確率で抽出し、R₀₂を抽出することはΔφが180°に近い結果を高確率で抽出することを意味する。 これは、即ち、R₀₁またはR₀₂のみを選んで取り出す操作が、位相変動(移相)量の差Δφで結果を選別することを意味する。

ただし、確率的な揺らぎを含むため、完全な選別ではなく、近似的な選別に留まる。 ここで、特定のΔφにおける干渉縞がcos²{(ωL＋Δφ)/2}＝{1+cos(ωL＋Δφ)}/2で表されるものとする。 これにD₁で検出される確率を掛けたものが、あらゆるΔφを考慮した干渉縞の式となり、それはcos²{(ωL＋Δφ)/2}・cos²(Δφ/2)となる。 これを展開すると{1+2cos²(ωL/2)+2cos⁡(ωL/2)・cos⁡(ωL/+Δφ)+cos⁡(ωL+2Δφ}/4となり、これをあらゆるΔφで平均化すると、後ろ２つの項の平均は０となるので、{1+2cos²(ωL/2)}/4＝{2+cos(ωL)}/4となる。 また、Δφ＝０の場合の干渉縞は、{1+cos(ωL)}/2＝{2+2cos(ωL)}/4で表される。

• Δφ＝０だけを抽出すると、干渉縞は{2+2cos(ωL)}/4で表される
• D₁と相関する（Δφが０に近い）データを抽出すると、干渉縞は{2+cos(ωL)}/4で表される

見れば分かる通り、Δφ＝０だけを抽出した場合に比べて、D₁と相関するデータはcos(ωL)成分がちょうど半分になっている その分だけ干渉縞が若干ぼやけるのである。 そのぼやけ方について、実測値と計算値のグラフを描く。 尚、実験結果を見ると分かる通り、光の強さは中心方向が強く、中心から離れるほど弱くなる指向性を持っている。 論文ではその指向性をsinc関数で表しているので、グラフでも同様に指向性を計算した。

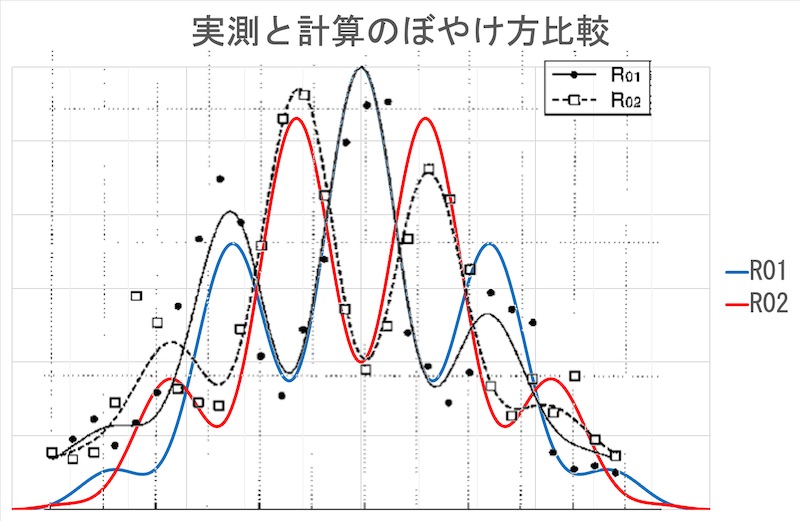
比較すると、実測と計算が比較的良く一致するように見える。 裾野部分では違いが見られるが、それは次のような原因であろう。

• 干渉縞のピークが中心からずれ、左右対称性も崩れている(実験装置の微細な位置誤差による)
• 指向性の計算式が実態と合っていない
• 計数値のばらつきが大きい(とくに裾野部分では目立つ)

ここで重要なことはR₀₁の最大部分におけるR₀₁とR₀₂の和と差である。 両者の差÷和は干渉縞の鮮明度を示している。 １であれば全くぼやけておらず、０であれば干渉縞が完全に消えている。 この実験では、計算上の鮮明度は0.5であり、実測でもほぼ同じ値となっている。 つまり、計算と実測でぼやけ方が一致しているのである。

---

このような計算になるため、R₀₁(赤)のみを選んで取り出すと次のようになる。

同様に、R₀₂(緑)のみを選んで取り出すと次のようになる。

以上踏まえると、R₀₁またはR₀₂のみを選んで取り出して干渉縞が復活することは、移相差に応じて結果を選別することで隠れた干渉縞を抽出できることを意味する。 つまり、干渉縞の復活は、経路情報の断念によってではなく、移相差選別によって実現しているのである。

先ほども説明した通り、R₀₁+R₀₂とR₀₃+R₀₄の違いはハーフミラーを通過するかどうかの違いだが、それが干渉縞に影響を及ぼすとは考えにくい。 量子もつれの影響を考慮しても、D₁〜D₄では可観測量の恣意的操作を行なっていないので、D₀の可観測量には影響を与える余地がない。 とくにD₃、D₄は、そのまま観測しているだけなので、D₀の可観測量が変わる余地がない。 D₁、D₂についても、D₀の可観測量に影響を与えそうにない。 確かに、ハーフミラーを通過するかどうかの違いにより、量子もつれの相方側で２つの経路を干渉させるかどうかの違いはある。 ここで、百歩譲って、相方側(D₁とD₂)を干渉させたせいでD₀の可観測量に影響を与えると仮定すると、R₀₁、R₀₂の干渉縞が消えるはずである。 しかし、R₀₁、R₀₂には干渉縞が認められることから、相方側(D₁とD₂)を干渉させるような仕組みがあっても、D₀の可観測量に影響を与えていないと推定できる。 D₁、D₂が可観測量に影響を与えないなら、尚更、相方側を干渉させずにそのまま光子を検出しているだけに過ぎないD₃、D₄がD₀の可観測量に影響を与えるとは考えにくい。 結果に影響を与える条件に違いが見られない以上、R₀₁+R₀₂もR₀₃+R₀₄も同じ現象になると考えるのが妥当である。 以上の通り、この実験においては、下側経路(D₁〜D₄に到達する経路)における測定や操作が、上側経路(D₀に到達する経路)の結果に影響を与えると考える理由が全くない。 科学に必須の前提である【同じ条件では同じ現象になる(同じ数式で記述できる)こと】を疑う必要が全くないのだから、当然、R₀₁やR₀₂と同様に、R₀₃やR₀₄も、移相差に応じて次の図のようになっていると推測できる。

ここで、逆に、量子もつれの相方側で２つの経路を干渉させた場合にのみ、D₀の可観測量に影響を与えた結果、干渉縞が復活すると仮定しよう。 その場合、D₁やD₂では偏光を操作していないため、D₀の偏光に影響を与えるとは考えにくい。 D₁やD₂で起きていることは位相関係に基づいた干渉であるから、D₀に与える影響は位相であり、BBOによって乱された位相が量子もつれによって回復すると考えられる。 当然、位相を持つからには波としての性質があることは言うまでもない。 つまり、D₁側とD₂側はミラーの前後で波動性を維持していることになる。 であれば、D₃側とD₄側も、少なくとも、ミラーの前までは波動性を維持しているはずである。 そして、ミラーによって波動性がなくなるとは考えにくいから、D₃側とD₄側もミラーの後で波動性を維持していると推測できる。 また、R₀₃、R₀₄の干渉縞が復活しないのは、量子もつれによる位相の補正がないからである。 であれば、位相が補正されればR₀₃、R₀₄の干渉縞は復活できるはずであり、位相に応じた２種類の干渉縞がお互いに相殺されて隠れていると推測できる。

もちろん、いくつかの仮定を置けば、R₀₃、R₀₄に隠れた干渉縞はないという理論も構築可能である。 しかし、そのような奇妙な仮定を置かなければならない合理的理由はないし、そのような奇妙な仮定の正しさを証明する根拠もない。 であれば、オッカムの剃刀を適用して、そのような奇妙な仮定は棄却されるべきだろう。

だから、移相差選別が可能であれば、干渉縞が復活できると予測できる。 残念ながら、R₀₃やR₀₄は、移相差の情報を得る方法がないため、図の赤と緑を分離することができない。 このように、この実験においては、経路情報と移相差選別の情報はどちらか一方しか得られないという相補性が成立している。 結果、経路情報を断念しない場合は、移相差選別を行うことはできず、干渉縞が復活できない。 しかし、相補性は、何らかの必然性があってそうなっているのか、ただの偶然なのかは定かではない。 確実に言えることは、干渉縞が見えないことは干渉がないことを示していないという至極当たり前の事実である。

以上まとめると次のとおりとなる。

• 経路測定してもしなくても干渉縞は見えなくなる
• 干渉縞が見えなくなる原因はBBOで初期位相がランダムに乱されるため(両経路の位相乱れ量は独立変数)
• 初期位相差が0°(または180°)に近い結果を確率的に抽出すると干渉縞が見えるようになる
• 経路測定すると初期位相差の確率情報(以下、「位相補正情報」)が手に入らない(干渉縞が復活しない)
• 経路情報を後から消しても位相補正情報は絶対に手に入らない(干渉縞は復活しない)

尚、D₃とD₄の検出結果が二重スリット実験の経路情報(which path information)として機能するかどうかについても検証する必要があるだろう。 というのも、次のような可能性が否定できないからである。

• 量子もつれの双方の通過スリットの検出結果が一致しない
• ２つの経路上の波が完全に分離されていないため、粒子の位置が入れ替わってしまう(波動性が粒子の位置を含めた可観測量を決めるため、２つの経路の波の干渉が粒子の位置に影響を与える)

これは次の装置により検証可能である。

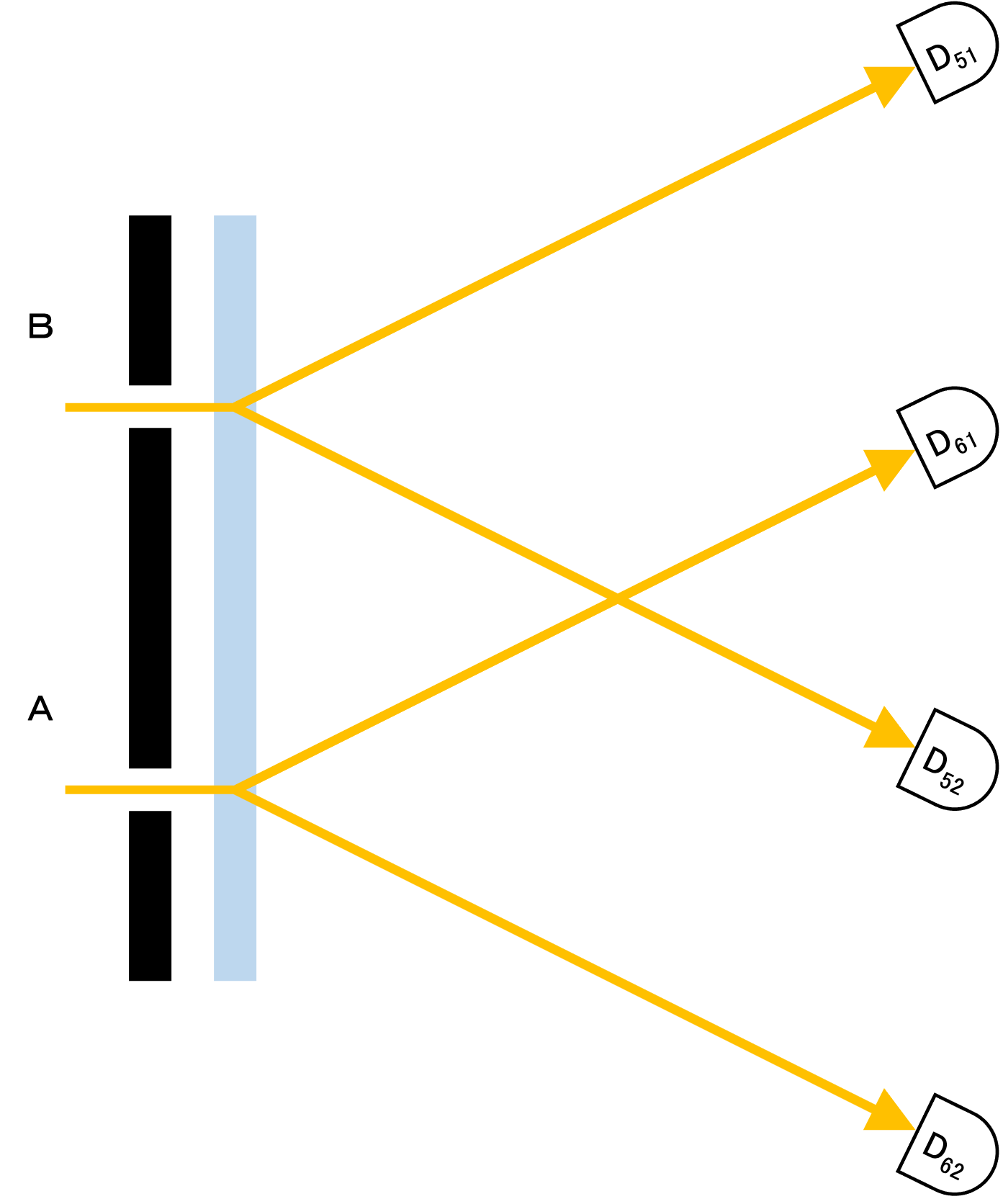
この装置のスリット幅は先ほどの装置と全く同じでなければならない。 この装置において、D₅₁とD₅₂の検出結果が高い確率(》50%)で一致し、かつ、D₆₁とD₆₂の検出結果も高い確率(》50%)で一致すれば、経路情報(which path information)として機能している。 逆に、双方とも一致確率がほぼ50%なら経路情報(which path information)として機能しない。 経路情報(which path information)として機能しなくても干渉縞が消えるなら、which path markerとして機能しないナンチャッテwhich path markerでも干渉縞が消えることになる。

まとめ 

この実験において経路情報と移相差選別のための情報のいずれか一方しか得られない相補性が成立している点は興味深い。 しかし、既に説明した通り、この実験の結果は全て古典力学の範囲で説明可能である。 常時成立する相補性は古典力学にない性質であるが、偶然の出来事として相補性が成立しているかのような格好になる現象であれば古典力学でも十分に起こりうる。 この実験では、如何なる場合にも相補性が成立することまでは証明できていないので、この実験における相補性が古典力学の範囲で説明できない現象とまでは言えない。

空想 

もしも、位相同期した３つの光子の量子もつれを作ることが可能なら、理論的には経路測定と干渉縞を両立できる。

• A1とB1で干渉測定
• A2とB2で位相測定
• A3とB3で経路測定

１つ目と３つ目の相関を取ることで通過経路を特定し、かつ、１つ目と２つ目の相関を取ることで干渉縞を得ることができる。 この実例として量子非消去実験を提唱する。

誤った説明の例 

誤った説明の事例は遅延選択量子消しゴム実験トンデモ解説に移動した。

参考 

• J.Wheelerの遅延選択実験