地震爆発論(笑)の反証
はじめに
このページは地震爆発論(笑)の一部である。
尚、地震爆破論(笑)には何の証明もない以上、それに対して反証を行う必要性は全くない。 しかし、容易に反証できるものは敢えて反証しておいても問題はなかろう。
「地震現象は地下において起きる水素の爆発(爆鳴気爆発:Detonation)である」理論
「地下水がマグマの高熱に接して起きる熱解離という作用」の後に「周囲の温度はいったん降下」して残るのは100%の水
石田昭氏の化学や物理の法則に対する無理解で紹介したように、石田昭氏は次のように主張する。
地震現象は地下において起きる水素の爆発(爆鳴気爆発:Detonation)であると考えるまったく新しい地震発振理論です。
その水素はどうして発生するのか、地下水がマグマの高熱に接して起きる熱解離という作用で発生するのです。 地下水だけでなく、マグマには大量の水が存在しています。 その水の化学反応で地震が発生するのです。
もう少し詳しくいいますと、水が解離する度合い(解離させる能力といってもいいでしょう。)は次の図に示すように温度と圧力で変化します。
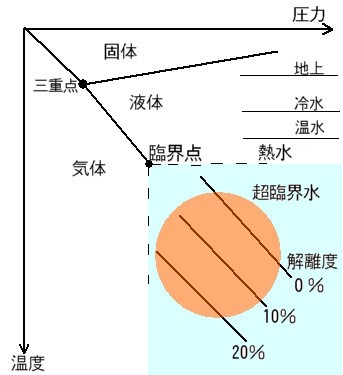
通常、地下ではこの解離度に応じて安定した状態、静穏な状態でおさまっています。 しかし、マグマが上昇したり、地殻に亀裂が入って圧力が変化すると、静穏が破られます。 すると状況は一変し、その場の熱と圧力によって決まる水の解離度に応じて、結合(爆発)したり、解離したりの反応が騒々しく起こります。
地震爆発論とは - 地震爆発論学会 地震爆発論学会解説 - 石田地震科学研究所
解離反応では①式から判るように熱が吸収されますので、周囲の温度はいったん降下し、爆鳴気と言われる解離ガスであってもすぐには爆発しません。
次のことは石田昭氏の化学や物理の法則に対する無理解でも突っ込んでいるので、ここでは深く言及しない。
- 石田昭氏は、化学を全く理解していない(笑)
- エネルギーを吸収させて水分子を水素分子と酸素分子に分離すること(2H2O→2H2+O2)と「水が解離する度合い」の図は関係がない
「地下水がマグマの高熱に接して起きる熱解離という作用」で爆鳴気が発生するとする主張は、熱力学第一法則(エネルギー保存則)には反しないが、熱力学第二法則(エントロピー増大則)に反する。 単に熱を加えただけでは2H2Oを安定した2H2+O2に変換できないことを以下に説明する。
2H2+O2におけるの水素原子や酸素原子の持つ位置エネルギーは、2H2Oにおける水素原子や酸素原子の持つ位置エネルギーよりも大きい。
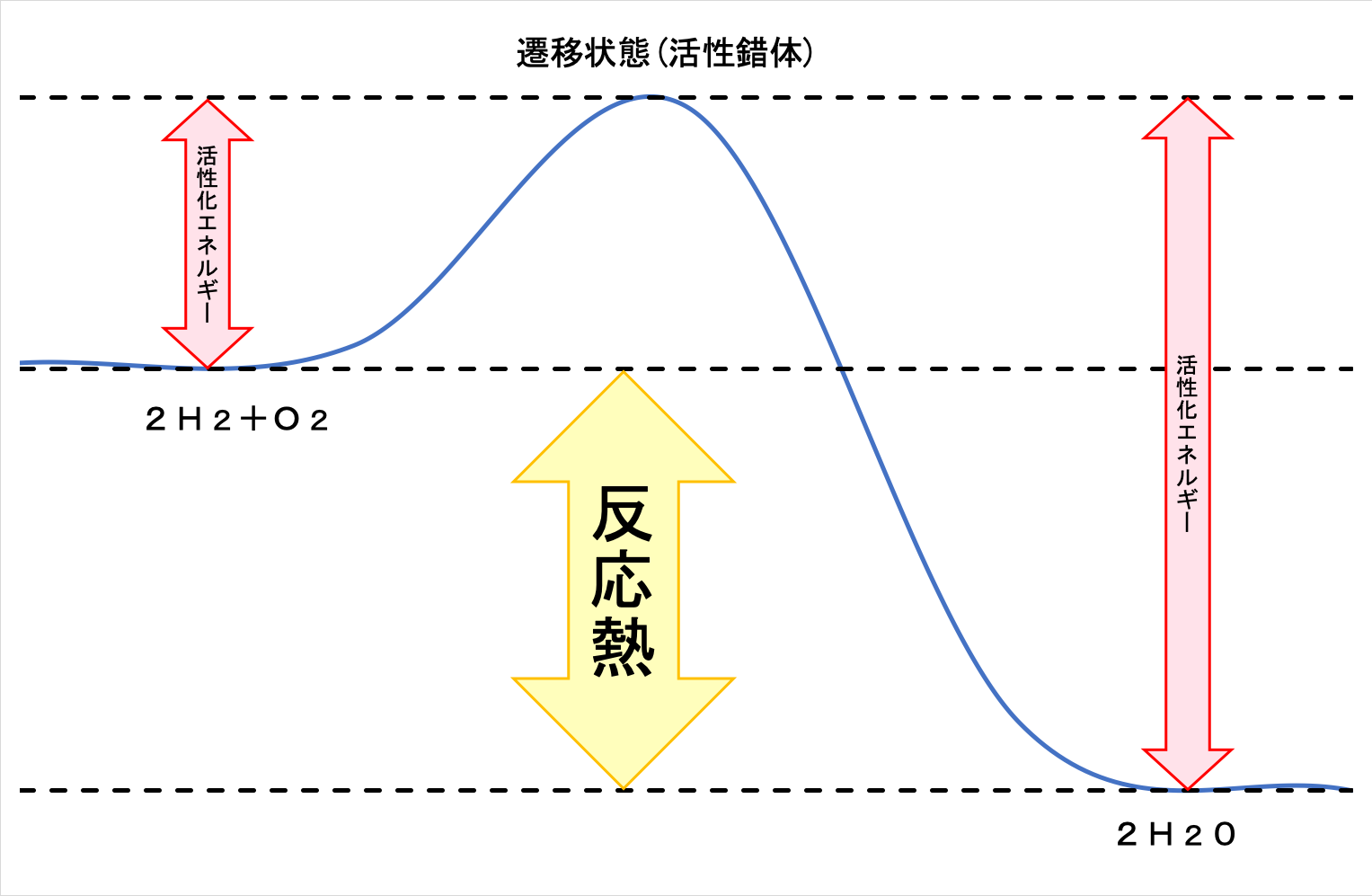
そのため、水素と酸素を燃焼させると、その差分が反応熱として発生する。 常温常圧では水素と酸素を混ぜても燃焼反応は起きないが、これは遷移状態(活性錯体)に変化させるために必要な活性化エネルギーを2H2+O2に与えられないからである。 ここで熱を加えると、必要な活性化エネルギーを2H2+O2に与えられることになる。 遷移状態(活性錯体)から、2H2Oに変化すれば、反応熱が他の2H2+O2に活性化エネルギーを与え、持続的に2H2+O2→2H2Oの反応が進行する。 一方で、この逆反応は容易に起こせない。 その理由として、まず、2H2+O2が必要とする活性化エネルギーよりも2H2Oが必要とする活性化エネルギーの方が大きいことが挙げられる。 そして、2H2Oが2H2+O2になるときに熱が吸収されることも重要である。 それら結果、活性化エネルギーが不足するために2H2O→2H2+O2の反応を持続することができない。
ここで、説明のために次のように言葉を定義する。
- 結合・分離両立温度域
- 2H2Oが必要とする活性化エネルギーも、2H2+O2が必要とする活性化エネルギーも与えられる超高温度域
- 結合のみ温度域
- 結合・分離両立温度域より低温で、2H2Oが必要とする活性化エネルギーは与えられないが、2H2+O2が必要とする活性化エネルギーは与えられる温度域
- 化学的安定域
- 結合のみ温度域より低温で、2H2Oが必要とする活性化エネルギーも、2H2+O2が必要とする活性化エネルギーも与えられない温度域
当然のことながら、「地下水がマグマの高熱に接して起きる熱解離という作用」は結合・分離両立温度域でしか起き得ない。 結合・分離両立温度域では、2H2+O2、遷移状態(活性錯体)、2H2Oのそれぞれの間の変化が頻繁に起こり得る。 その結果、時間の経過とともに、2H2+O2、遷移状態(活性錯体)、2H2Oの比率が一定値に落ち着く定常状態に移行すると予想される。 定常状態では、発生する熱と吸収される熱の合計値が等しい。 では、結合・分離両立温度域から「周囲の温度はいったん降下」するとどうなるか。
結合のみ温度域に達すると、2H2O→2H2+O2の反応が生じなくなるが、2H2+O2→2H2Oの反応は生じる。 この場合、2H2+O2→2H2Oの反応により発生する反応熱により、2H2+O2→2H2Oの反応がなくなるまで、すなわち、全ての2H2+O2が2H2Oに変化するまでは、温度低下が遅くなる。 爆鳴気であれば、2H2+O2→2H2Oへの反応は一瞬で終わるので、2H2+O2を残したまま結合のみ温度域を通過することはできない。 その結果、化学的安定域に達した時、全ての2H2+O2は2H2Oに変化している。
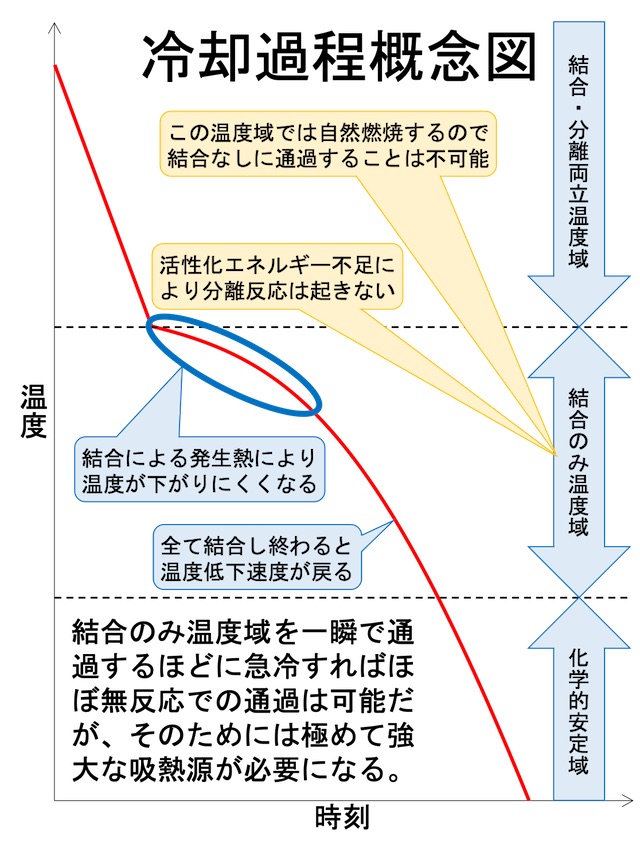
理論的には、結合のみ温度域を通過する時間を無視して良いくらい結合・分離両立温度域から化学的安定域まで瞬時に冷却できれば、一定割合の2H2+O2を残したままにすることは可能に思える。 しかし、そのためには、マグマの熱を一瞬で奪わなければならない。 石田昭氏の化学や物理の法則に対する無理解で説明した通り、石田理論では、「地下水がマグマの高熱に接して起きる熱解離という作用」で発生した爆鳴気は核爆弾を上回るエネルギーを受け取っているので、その熱を一瞬で奪うには極めて強大な吸熱源が必要になる。 地下にそのような強大な吸熱源が存在するなら、地質学界を揺るがす大発見となろう。 しかし、石田理論では、そのような吸熱源については一言も触れられていない。 主流学説にも石田理論にも登場しない以上、そのような吸熱源は存在しないと考えるべきだろう。 よって、結合のみ温度域を通過する時間を無視して良いくらい結合・分離両立温度域から化学的安定域まで瞬時に冷却することは不可能である。
以上の通り、化学の基本法則に照らせば、「地下水がマグマの高熱に接して起きる熱解離という作用」で爆鳴気を発生させることは不可能である。
また、地震爆発論を否定する方の中には、様々な反論を書いて、爆発論を笑う方もあります。
一例を挙げれば(参考)、
「熱解離という作用」の後に「周囲の温度はいったん降下」して残るのは100%の水である。 ・・・ということはありません。 解離した酸素と水素の混合ガスが残ります。 結合反応(爆縮・Implosion)が無ければ水にはなりません。
石田昭氏は、化学の基本原理を無視しても断言すれば現実になると思っているのか(笑)。 「ということはありません」「が残ります」「にはなりません」等の根拠を示さない断定は、石田昭氏の空想世界では何らかの意味を為しているのかもしれない。 しかし、現実世界では、化学や物理の基本原理に従って説明しなければ意味がない。 化学の基本原理に沿った反応を回避する何らかの仕組みを説明することもなく、化学の基本原理に沿った反応が起きないなんて断言するのでは、オカルトや超能力と何ら変わらない。
既に説明した通り、「周囲の温度はいったん降下」するなら、水素と酸素が反応しない温度域に下がる前に、結合のみ温度域(2H2Oが必要とする活性化エネルギーは与えられないが、2H2+O2が必要とする活性化エネルギーは与えられる温度域)を必ず通過する。 結合のみ温度域では、2H2+O2が必要とする活性化エネルギーが与えられるから、「結合反応」が起きないことはあり得ない。 一方で、結合のみ温度域では、2H2Oが必要とする活性化エネルギーは与えられないため、水が「酸素と水素の混合ガス」になる反応は起きない。 結合のみ温度域を通過する以上は、化学の基本理論に沿う限り、「解離した酸素と水素の混合ガスが残」ることはあり得ないのである。
「参考:(節操のないサイト「反証」より)」と書いてあるから、ここを読んで主張しているはずなのに、ここに書いてあることに一切反論しないで、結論を断定形でゴリ押しするだけとは呆れ返る他ない。 敢えてリンクを貼らなかったのは、「反証」を見られては困るからなのだろう。 つまり、石田昭氏は、何ら反論をしていないことを自覚しているのだ。
「水素の爆発」で「体積が減少」するためには反応前温度が6427(kelvin)以上必要
石田昭氏の化学や物理の法則に対する無理解で紹介したように、石田昭氏は次のように主張する。
しかしこれはダイナマイトの爆発のようなものが固定観念としてあるためであって、水素の爆発ではそのようなことにはなりません。 下の図にあるようにボイラーが破壊されるときの平衡破綻型爆発ようなExplosionと水素と酸素の結合で体積が減少するImplosionがほぼ同時に起きることが、地震現象特有のメカニズムであります。
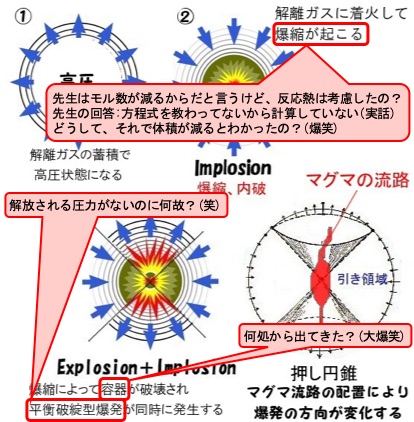
ダイナマイトの爆発ならば頷ける理屈ですが、水素爆発(Detonation)というのは水素と酸素の化学反応のことであり、体積が減少することが大きな特徴です。 ボイラー爆発のような平衡破綻型の爆発(Explosion)と体積が減少する爆縮(Implosion)が同時に生じていることが複雑なところなのです。
地震爆発論とは - 地震爆発論学会 地震爆発論学会解説 - 石田地震科学研究所
そんな中で、地震時の「押し」と「引き」を説明するには、平衡破綻型爆発(マグマの移動を契機として破綻が崩れて爆発することで「押し」が生まれる)というボイラーの破壊に似た現象と、酸素と水素が結合して体積が減少する(少なくとも、3モルから2モルに縮小するので「引き」現象を生じるはず)というアイディアが生まれたのですが、その正否について当時の専門家からも「よく分からない」と言われました。
②酸素と水素の反応は、結合する場合は発熱反応ですし、解離する場合は吸熱反応ですから、熱による影響はもちろんあります。 しかし、超臨界状態の化学については蒸気爆発の専門家も「よくわからない」ということですし、教えていただけませんでした。 よって、その反応を方程式に従って計算はしておりません。
次のことは石田昭氏の化学や物理の法則に対する無理解でも突っ込んでいるので、ここでは深く言及しない。
- 「爆縮(Implosion)」とは、爆発の圧力で物質を圧縮する技術のことであって、爆発によって自然に「体積が減少する」現象ではない
- 「計算はしておりません」のに、どうやって、「水素と酸素の結合で体積が減少する」とわかったのか
- 石田昭氏の言う、「専門家」とは、トンデモ本を出しているだけの疑似科学仲間にすぎない
「酸素と水素が結合して体積が減少する」かどうかは、理想気体の状態方程式から容易に計算可能である。 では、「水素と酸素の結合で体積が減少する」場合の爆鳴気の反応前温度を求めてみよう。 ここで、水素と酸素が化合する前の変数の添え字をS、反応熱を考慮した場合の化合後の変数の添え字をEとする。 もしも、 pEVE=pSVS であれば、化合後の体積は膨張も減少もしない。 そして、化合後の体積が減少するためには、 pEVE<pSVS でなければならない。 以下、 pS=pE の場合を想定する。 水の反応式から nE=(2/3)×nS である。 また水の反応熱と定圧モル比熱から、 TE= TS+ΔrH/CP° となる。 よって、 pEVE=nE×R×TE=(2/3)×nS×R×(TS+ΔrH/CP°) となる。 これを pEVE<pS VS に代入すると、 TS>2×ΔrH/CP° が得られる。 水分子1個あたりの反応熱 ΔrH は約241kJ/molであり、水の定圧モル比熱 CP° は約75J/(mol・kelvin)であるから、 TS>6427(kelvin) となる。 つまり、爆鳴気の反応前温度が6427(kelvin)以上でないと、「水素と酸素の結合で体積が減少する」ことはあり得ない。
温度が6427(kelvin)以上の爆鳴気が化合せずに安定して存在できるのか。 常識で考えれば、反応前温度が6427(kelvin)もあれば、自然発火してしまうので、化合せずに安定して存在できるわけがない。 だから、爆鳴気の反応前温度が6427(kelvin)以上であるわけがないので、「水素と酸素の結合で体積が減少する」ことはあり得ない。
地下水が核を超える熱エネルギーを受け取れば水蒸気爆発が起きる
石田昭氏の化学や物理の法則に対する無理解で解説した通り、地震爆発論(笑)の地震発生原理では、地下水がマグマから核爆弾のエネルギーを超える熱エネルギーを受け取ることになる。 また、「地下水がマグマの高熱に接して起きる熱解離という作用」は、常温での水の沸点を遥かに超える超高温でしか発生し得ない。 であれば、核爆弾のエネルギーを超える地下水の熱エネルギーの大半は膨張エネルギーに変換される。 地下水を含む地層が、それほど強大な圧力に耐えられるわけがない。 だから、地下水が核を超える熱エネルギーを受けたなら、水蒸気爆発、もしくは、マグマ水蒸気爆発が発生するはずである。 それだけの大爆発が生じれば、当然、その瞬間に、周囲の地層は丸ごと吹き飛ぶか、少なくとも、強大な亀裂が生じるはずである。 であれば、マグマに曝された地下水は水蒸気となって周囲に霧散するから、その後の地震爆発論(笑)の地震発生原理の過程まで到達し得ない。 よって、核でもビクともしない頑強な地層でもない限り、地震爆発論(笑)の地震発生原理は成立し得ない。
余震発生メカニズムと観測される余震が全く違う
通常、地下ではこの解離度に応じて安定した状態、静穏な状態でおさまっています。 しかし、マグマが上昇したり、地殻に亀裂が入って圧力が変化すると、静穏が破られます。 すると状況は一変し、その場の熱と圧力によって決まる水の解離度に応じて、結合(爆発)したり、解離したりの反応が騒々しく起こります。 この爆発が地震の真相です。
これが地震現象の正体です。 したがって解離している層が安定するまで、地震は繰り返し起こります。 これが大地震の後では解離層が大きく乱されるために、なかなか安定しない原因です。 また大地震ほど余震が止まらない原因です。 小さな地震ではすぐに解離層が安定するので、余震の数も少ないわけです。
「マグマが上昇したり、地殻に亀裂が入って圧力が変化する」ことについて、次の2通りで考察してみる。
- 「静穏が破られ」る要因として大きなウェイトを占めている
- 「静穏が破られ」る要因として大きなウェイトを占めていない
前者の場合は、大地震が生じれば、「地殻に」巨大な「亀裂が入」るため、大きく「静穏が破られ」るはずである。 ここで、地下水やマグマが十分にある状況であるなら、「大地震の後では」大地震直前以上に「解離層が大きく乱される」ことになるので、本震の後に本震以上の大きな地震が発生しないとおかしい。 逆に、地下水やマグマが十分にない状況(「マグマが上昇」する量が不十分な状況を含む)なら、すぐに「解離している層が安定」するため、余震は直ぐに収まるはずである。 であれば、前者の場合は、地震の発生パターンは次のようになるはずである。
- 大地震の直後に極短期間で余震が収束する(最初の大地震で地下水やマグマが不足するケース)
- 大地震の直後に段階的に大きくなる地震が数回発生した後に極短期間で余震が収束する(数回の大地震で地下水やマグマが不足するケース)
- 大地震の直後に段階的に大きくなる地震が発生した後、規模や頻度が減衰しない余震が長期に継続する(地下水やマグマが有り余っているケース)
大地震の直後に更に大きな地震が生じるケースは非常に少なく、近年、M5以上の地震の直後に更に大きな地震が発生したケースは次のとおりである。
| 発生年 | 震源 | 本震 | 前震 |
|---|---|---|---|
| 1891 | 濃尾 | M8.0 | M6.0 |
| 1960 | チリ | M9.5 | M8.2 |
| 2003 | 宮城県北部 | M6.4 | M5.6 |
| 2008 | 茨城県沖 | M7.0 | M6.4 |
| 2010 | 福島沖 | M6.9 | M5.5 |
| 2011 | 東北地方太平洋沖 | M9.0 | M7.3 |
| 2013 | ソロモン諸島沖 | M8.0 | M6.0以上 |
| 2016 | 熊本 | M7.3 | M6.5 |
百万歩ほど譲って、これらの地震を3番目のケースと認定したとしても、世界中で発生している地震の極一部に過ぎない。 また、多くの大地震では余震が長期間続いているので、1番目と2番目に当てはまるケースが見当たらない。 以上の通り、前者の場合は、理論的に予測される地震の発生パターンと実際の地震の発生パターンが大きく食い違っている。 もちろん、実際の現象の多くが理論と一致して、かつ、一部の現象だけが食い違うだけなら、その理論を支持しない理由にはならない。 しかし、実際の現象の殆どが理論と食い違い、かつ、好意的に解釈した時にのみ極一部の現象だけが一致しているなら、その理論を支持する理由がない。
では、後者ではどうなるか。
地下の圧力を急激に上げたり、下げたりという操作をすることは、離れた場所にも圧力変化が伝播します。 当該の貯留空間は解離が生じるような高い温度でなくても、伝播先の空間では解離条件が変化し、“解離ガスの爆発”という現象を引き起こしてしまう可能性があります。
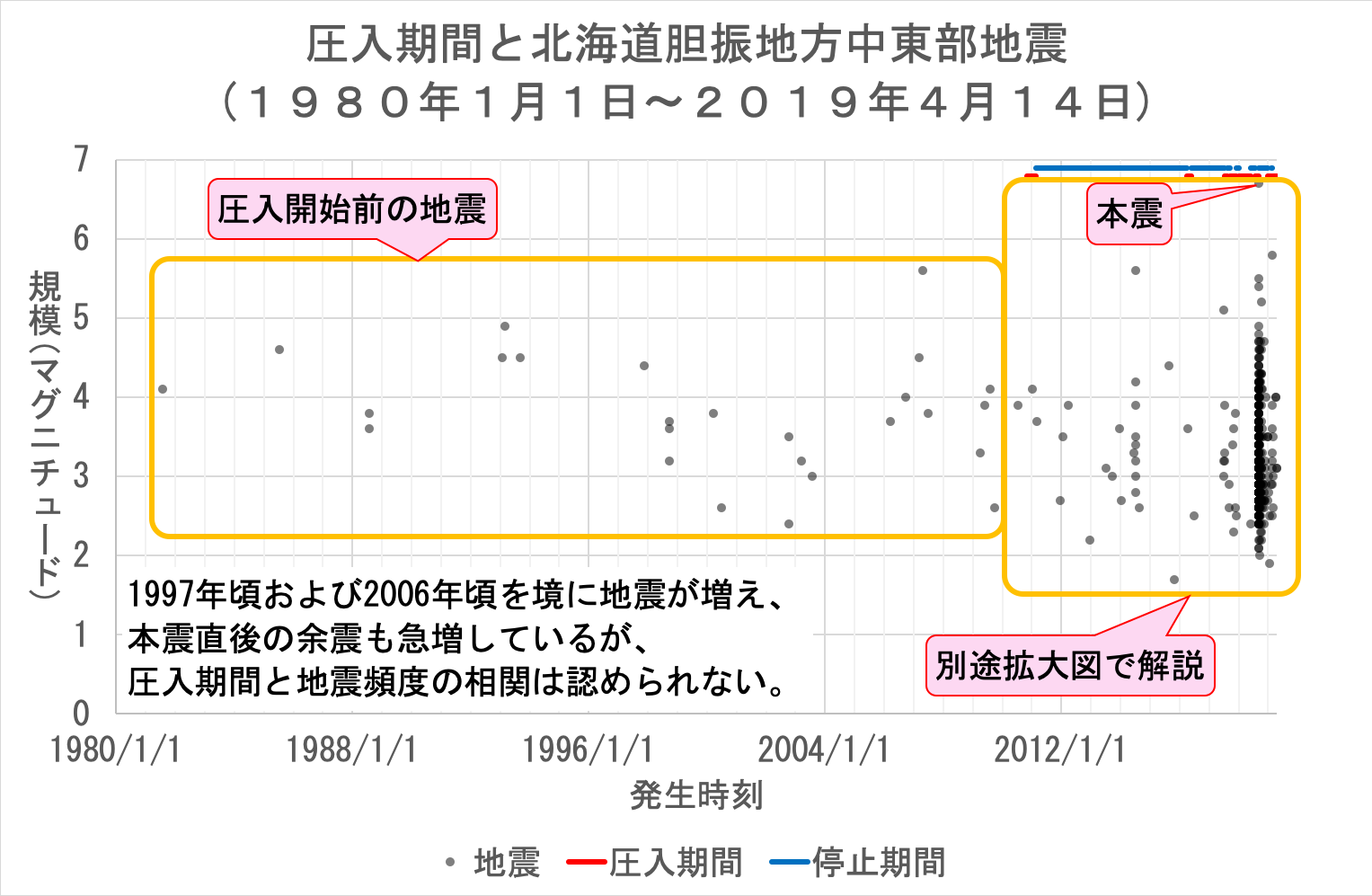
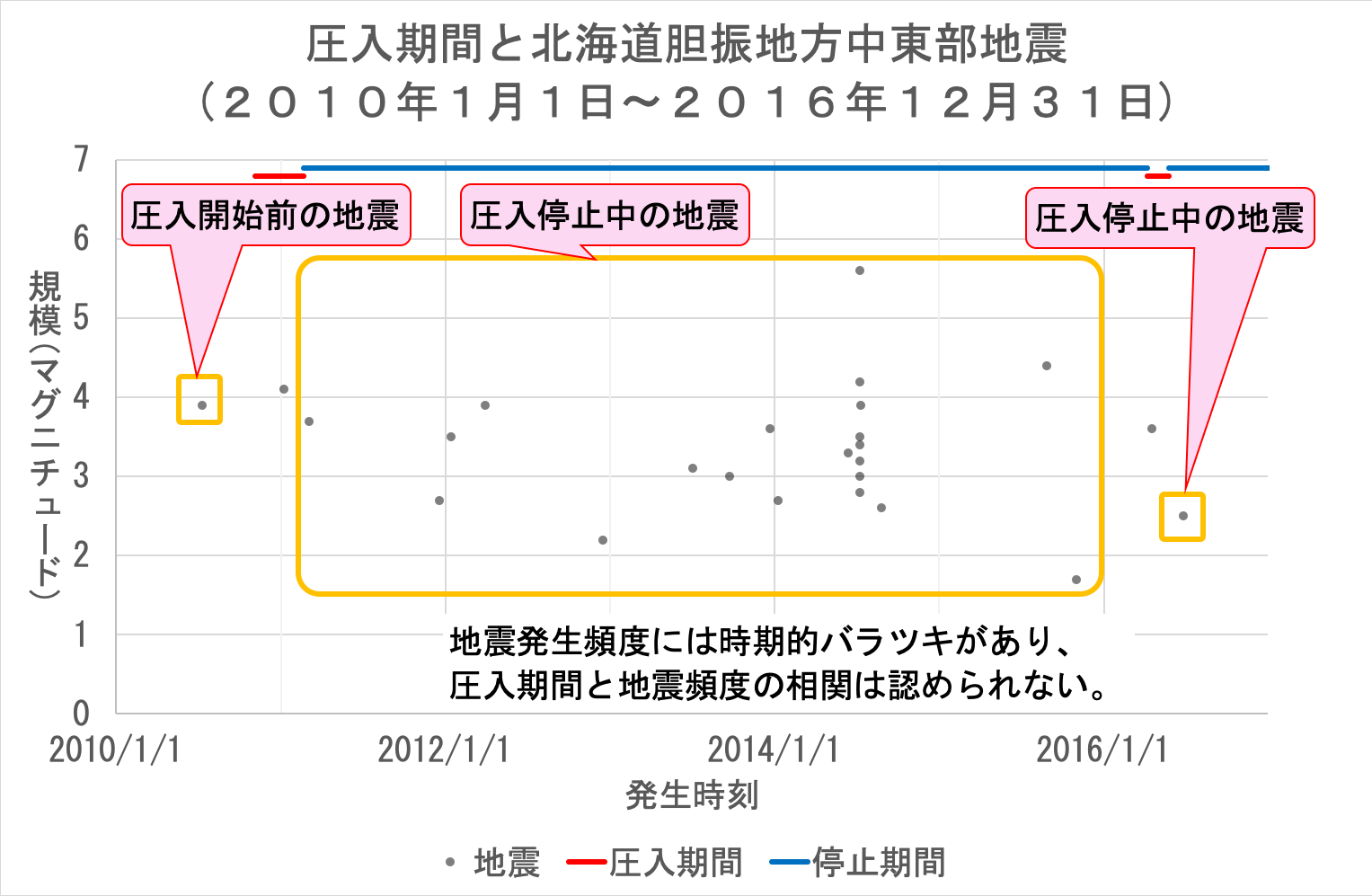
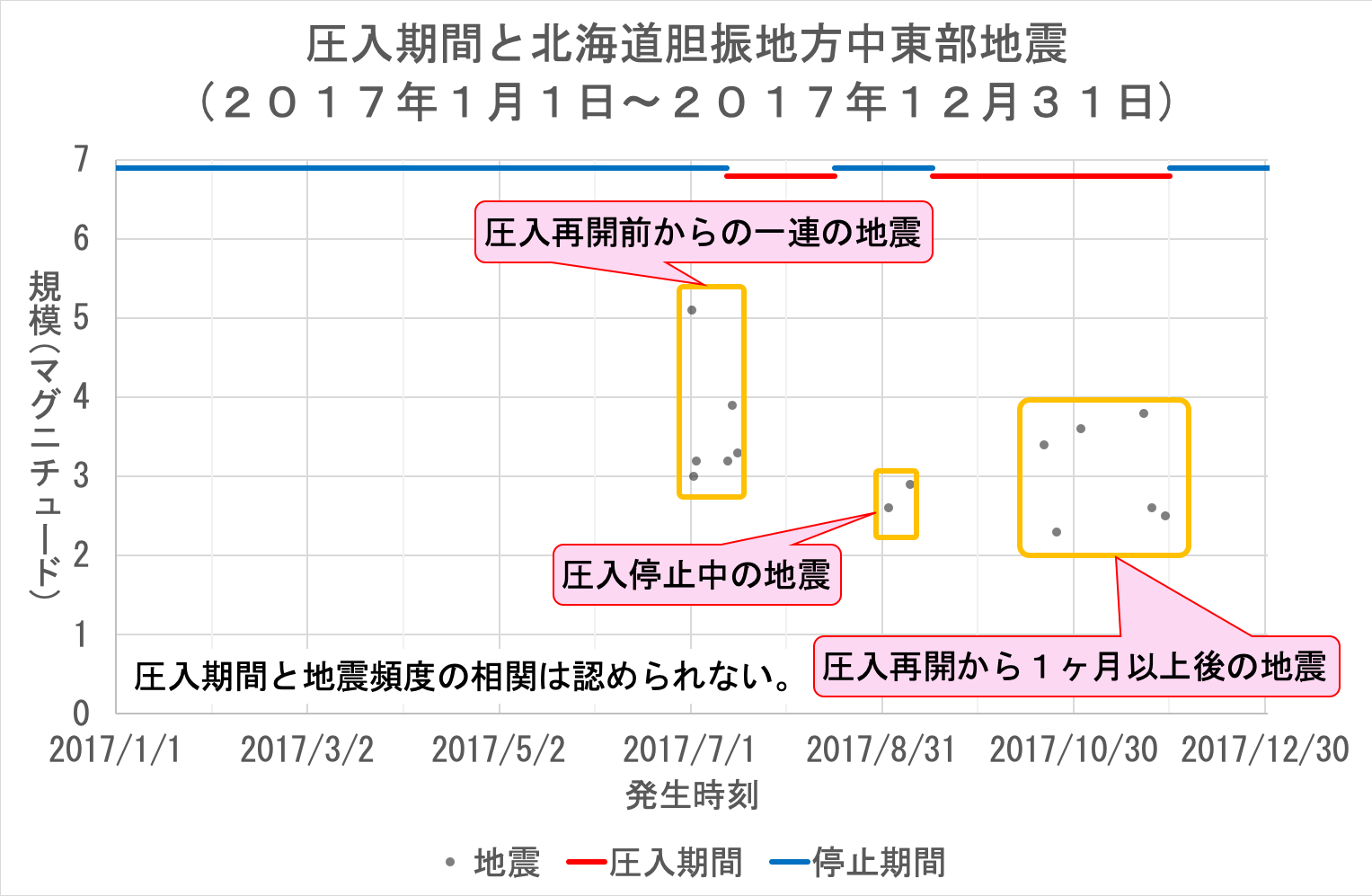
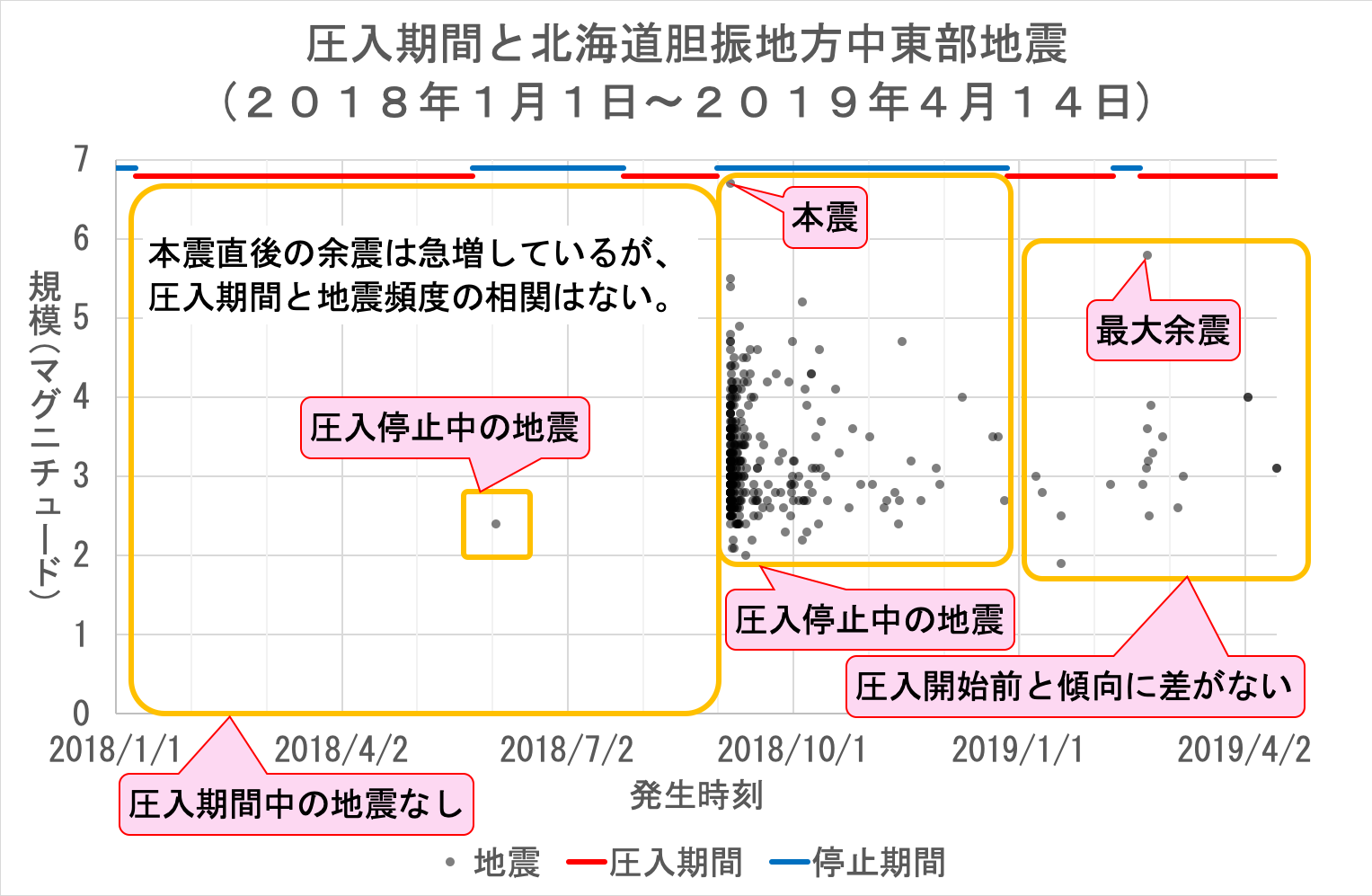
後者では圧入井の圧力変化が「静穏が破られ」る要因として大きなウェイトを占めているはずである。 それならば、「解離層が大きく乱されるために、なかなか安定しない」状況は、「大地震の後」に限らず、「地下の圧力を急激に上げたり、下げたりという操作」をした直後には常に生じるはずである。 であれば、地震発生頻度は直前の地震の規模ではなく「地下の圧力を急激に上げたり、下げたりという操作」の程度で決まるはずであり、「大地震ほど余震が止まらない原因」という説明は成立しない。 だから、「大地震の後」に余震が頻発するのと同様、「地下の圧力を急激に上げたり、下げたりという操作」をした後にも地震が頻発しなければおかしい。 実際の北海道胆振中東部の地震では次のようになっている。
平成23年度第2回CO2固定化・有効利用分野評価検討会 技術に関する施策・事業評価報告書 第3章 A 二酸化炭素削減技術実証試験(プロジェクト)の概要(中間評価) - 経済産業省 お知らせ - 日本CCS調査株式会社 震度データベース検索 - 気象庁
平成23年度第2回CO2固定化・有効利用分野評価検討会 技術に関する施策・事業評価報告書 第3章 A 二酸化炭素削減技術実証試験(プロジェクト)の概要(中間評価) - 経済産業省 お知らせ - 日本CCS調査株式会社 震度データベース検索 - 気象庁
平成23年度第2回CO2固定化・有効利用分野評価検討会 技術に関する施策・事業評価報告書 第3章 A 二酸化炭素削減技術実証試験(プロジェクト)の概要(中間評価) - 経済産業省 お知らせ - 日本CCS調査株式会社 震度データベース検索 - 気象庁
平成23年度第2回CO2固定化・有効利用分野評価検討会 技術に関する施策・事業評価報告書 第3章 A 二酸化炭素削減技術実証試験(プロジェクト)の概要(中間評価) - 経済産業省 お知らせ - 日本CCS調査株式会社 震度データベース検索 - 気象庁
百万歩ほど譲って、本震の後に余震が急増していることを「地下の圧力を急激に上げたり、下げたりという操作」をしたことによって地震が急増したと解釈したとする。 しかし、それ以外にも「地下の圧力を急激に上げたり、下げたりという操作」は何度も行われているが、それに伴って地震が増加する現象は全く見られない。 よって、後者の場合も、理論と実際が一致しない。 以上の通り、「大地震ほど余震が止まらない原因」を「解離している層が安定するまで、地震は繰り返し起こります」とする余震発生原理は実際に起きた地震と大きく食い違っている。
石田理論は余震域の広がりとも矛盾する。 例えば、2018年の北海道胆振東部地震では、余震域が南北に±約20kmの範囲に広がっているが、これは地震の結果として断層が発生したとする石田理論と合わせることが可能である。 しかし、東西に約10km以上の範囲に広がっていることは、石田理論では説明がつかない。 2004年の新潟県中越地震や2007年の新潟県中越沖地震は2018年の北海道胆振東部地震よりも震央分布が真円に近い。 地震波は全方位に広がって伝わるため、伝搬エネルギーは距離の自乗に反比例して減衰する。 よって、地震によって「マグマが上昇したり、地殻に亀裂が入って圧力が変化する」ことが引き起こされる現象は、震源に近いほど発生しやすく、かつ、震源に遠いほど発生しにくくなる。 10km以上離れれば伝搬される地震エネルギーはかなり小さくなっているので、それによって「地殻に亀裂が入」ることはあり得ない。 ただし、地震の結果として断層が発生したとする石田理論であれば、断層が発生した方向については多少遠くとも「地殻に亀裂が入」る余地がある。 しかし、断層方向に力が逃げてしまうため、それ以外の方向の遠距離に「マグマが上昇したり、地殻に亀裂が入って圧力が変化する」ことが説明できない。 石田理論では、地震の結果として発生した断層に沿った細い線上の余震域になるはずである。 しかし、実際の地震では震央分布は楕円状に広がっている。 もしも、細い線上の余震域が発生した事例があれば、珍しい事例として地質学会に報告されるだろう。
「殆どのエネルギーは二層構造の地殻内部を屈折と反射を繰り返しながら、伝播している」理論
石田昭氏の化学や物理の法則に対する無理解で紹介したように、石田昭氏は次のように主張する。
しかし、それは前述のビデオにあるように、粘弾性体としてのマグマが爆発的な振動(高周期成分波)の一部を伝播させているだけで、殆どのエネルギーは二層構造の地殻内部を屈折と反射を繰り返しながら、伝播しているのです。
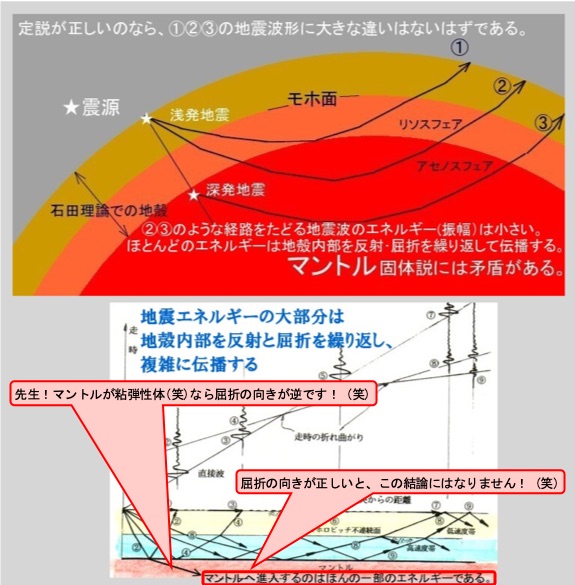
これが容易に反証できることを次に示す。
シャドーゾーンが全く説明できない
「殆どのエネルギーは二層構造の地殻内部を屈折と反射を繰り返しながら、伝播している」理論では、103°以上の領域でP波やS波が極端に小さくなることや、143°以上でまたP波の大きさが復活することをまったく説明できない。 石田昭氏による情報歪曲等で紹介するように、石田昭氏は「よく目を凝らしてみると、わずかではあるが縦波が認められる」を「影のゾーンは存在しない」にすり替えているが、そのような詭弁では「影のゾーン」で地震波が極端に弱くなることを否定できない。
実際はどうなのか、というのが一連の新地震理論であります。 モホロビッチ不連続面の下に地震波を伝播させる、橄欖岩から構成された固く、緻密な地殻第二層が存在するのです。 103度まではそこを通過して伝播していきます。 途中で、玄武岩からなる第一層へも少しずつ浮上して、台地を揺るがせていきますから、103度付近で、減衰してしまうのです。 143度から180度の間へは、地球内部を通過して伝播していく地震波が到達しているのです。 こうした理由で、「地震波の影」ができるのです。
距離による減衰によって「103度付近で」ほぼゼロになるとすれば、境界が曖昧になり「103度」という数値が測定できるわけがない。 地殻は球対称ではなく、山があったり海があったり地域毎に形が不均衡であるので、地殻による減衰量も地域によって変わるはずである。 しかも、地震毎にマグニチュードも違うため、自然減衰では、ほぼゼロになる点が「103度付近」であることが説明できない。 そもそも、自然減衰でゼロになっているだけならシャドーゾーンなどとは呼ばれない。 「103度付近」を境に、それまであった地震波が急激になくなる(小さくなる)からシャドーゾーンと呼ばれるのである。 しかし、「103度付近」で、それまでにない急激な減衰が発生する科学的に妥当な原因を石田昭氏は何も示していない。 また、「143度から180度の間」以外に「地球内部を通過して伝播していく地震波が到達」しない科学的に妥当な原因についても石田昭氏は何も示していない。 よって、「103度付近で、減衰してしまう」「143度から180度の間へは、地球内部を通過して伝播していく地震波が到達している」では、原因不明だが不思議なことが都合良く起こると言っているだけの非科学的なファンタジーである。
石田理論では、中心核を設定する必要はありません。 【溶融マントル内を直進する地震波(海震の項で説明したように、直進波だけがエネルギーを所有することができる)と、地殻内を潜水泳法のような形で減衰するまで進行する地震波の到達限界との間に「影の領域」ができると考えています。】 当然橄欖岩という伝播速度の速い領域を通ってくる潜水泳者のほうが早く到達します。
(石田)
上記の黒字部分の解釈を撤回します。
「直進波だけがエネルギーを所有することができる」という説は撤回されたようなので、「143度から180度の間へは、地球内部を通過して伝播していく地震波が到達している」ことの説明が全くできていない。 まあ、「直進波だけがエネルギーを所有することができる」などのファンタジー法則は撤回して当然だろう。
マントルが熔融しているしていると主張しながら「伝播速度の速い領域」と主張するのであれば、剛性率の低い方が「伝播速度の速い」と主張することになり、これは既存の物理の法則と全く逆になる。 そのような新法則を提示するなら、自ら実験等で証拠を示すべきだろう。
左の図は地殻の厚さが100kmと仮定し、地殻最下端部のP波の伝播速度を8km/s、マントル最上部でのP波の伝播速度を3km/sとして計算した屈折関係図です。 震源はごく浅い場所と仮定します。 右の図は地震波の記録中に示す①~③の意味を示す図です。
P波が最大の入射角90度で進入すると、中心角度λは10.2度、屈折角度θrは19.5度となります。 90-19.5=70.5度の角度には、地震波は進入できません。 したがってグーテンベルグが仮定したような伝播経路をとることはありません。
地球内部へ侵入した波は地球内部で伝播速度が増大するものと思いますが、現状では明確には分かりません。 しかし、やがて「固液複合系の力学物性」というような研究が進めば明らかになってくるものと期待しています。
模式的には黒矢印で示すような範囲内をP波は進行していると思います。 それ以外のP波及びS波は赤矢印で示すような伝播経路とるものと考えられます。 なお、地球内部から地殻に達した点A’ではPKSに類似するようなS波が生まれる可能性がありますし、B点では別のP波が地球内部に進入する可能性があります。 もちろん、地殻内部でも(少なくとも二層以上で)伝播速度の違いによる屈折現象がおきています。
石田昭氏は、ようやく、剛性率が低い方が波が遅くなることに気づいたようだ(笑)。 そして、「143度」側の境界を説明する理屈を思いついたようだ。 しかし、その理屈にも次のような欠陥がある。
- 震源の深さが100m以下の場合は、深さによって境界が20.4°変化する
- 震源の深さが100m以上の場合は、シャドーゾーンが消滅する
細かいツッコミをすると、「屈折角度θr」はSin-1(3/8×sin90°)であるので「19.5度」ではなく約22°であろう。 マントル内部を地震波が直進すると仮定すると、深さ0mの地震はこの条件で、マントル内部を通った地震波はλ×2+(90-θr)×2=156.4°の場所に到達する。 「143度」の場所に到達するためには、マントル内部で図の方向に大きくカーブする必要がある。 マグマオーシャンの表面だけが冷え固まったとする地震爆発論(笑)の考え方ではカーブの向きが逆のはずであるが、そこは大目に見よう。
ここで、石田理論における「地殻」の最下部に相当する深さ100mで起きた地震を考える。 その場合、λ=0°となるので、10.2×2=20.4°だけ到達角度が小さくなる。 平均を「143度」となるようにしても、143±10.2°、すなわち、132.8〜153.2°となる。 これでは、通常、約140°と言うことはあっても、約143°とは言わない。 つまり、深さによる角度変動量が多すぎるのである。
震源の深さが100m以上になると、マントル内部を通った地震波の到達できない領域がなくなる。 それでは、シャドーゾーンが完全に消滅する。 よって、地震爆発論(笑)ではこの補助理論を採用してもシャドーゾーンを説明することはできない。
これは、典型的な疑似科学理論における辻褄合わせの失敗例である。 これは、科学の条件を満たした理論の辻褄合わせとは全く違う。 科学理論において、一見、突拍子も無いように見える仮定は、現実との辻褄合わせに不可欠なものである。 だからこそ、それだけで全ての現象が説明できないとしても、どこかに辻褄の合う答えが存在するのである。 科学理論では、実在する法則を人間が探しているだけなのだから、答えが見つかることは必然である。 しかし、疑似科学理論における突拍子も無い仮定は、現実と辻褄を合わせていない創作理論に過ぎない。 猿がタイプライターをデタラメに叩いてシェークスピアの作品が偶然できるわけがない。 それと同じように、創作に創作を重ねて偶然に現実に合う理論ができるわけがない。 現実にない理論を人間が作り出そうとするのは無駄なことである。
尚、どうでも良いが、通常、角度にはθやφ等を使うのが普通である。 波の理論ではλは波長に使うことが多いので、角度の変数には使わない。 土木工学では角度にλを使うのが普通なのか。
走時の理論上限最速値が実測値より遥かに遅い
「殆どのエネルギーは二層構造の地殻内部を屈折と反射を繰り返しながら、伝播している」理論では、地球の大きさに比べて非常に薄い膜の中を波が伝搬することになる。
左の図は地殻の厚さが100kmと仮定し、地殻最下端部のP波の伝播速度を8km/s、マントル最上部でのP波の伝播速度を3km/sとして計算した屈折関係図です。
石田昭氏の仮定「地殻の厚さが100km」(石田昭氏はリソスフェアまでが地殻だと誤解している模様)に基づいて、地球全体に占める地殻の割合を下の図に示す。

この薄い膜内の波の伝搬は光ファイバーと似ていると推測できる。
ここで、石田昭氏の仮説に基づいて、伝搬時間の理論上の最速到達値(それよりも遅くなる可能性はあるが、決して、速くはならない)を求める。 まず、仮に、「二層構造の地殻内部を屈折と反射を繰り返しながら、伝播している」P波は、地殻に沿って円弧状に伝搬していくものとする。 本当は、「屈折と反射を繰り返しながら」であれば、地殻内をジグザグに進行することになる。 当然のことながら、地殻に沿って円弧状に伝搬するよりも、ジグザグ進行の方がP波の到達は遅い。 また、ここでは、P波は「地殻最下端部」のみを伝搬するものとする。 石田昭氏は、地殻下層は地殻上層はよりも伝搬速度が速いとしているので、当然、「地殻最下端部」のみを伝搬する方が、「二層構造の地殻内部を屈折と反射を繰り返しながら、伝播している」よりも、P波の伝搬速度は速い。 この場合の伝搬時間は、マントル半径×θ(radian)÷【「地殻最下端部」の伝搬速度】となる。
さらに、もう一つの経路として、一度も反射せずにマントル内部を通る経路を考える。 無反射経路を想定する理由は、反射を考慮すると「二層構造の地殻内部を屈折と反射を繰り返しながら、伝播している」場合が最速となり、先ほどの計算と同じものを求めることになって、計算の意味がなくなるからである。 石田昭氏の仮説では、マントルよりも地殻の方が伝搬速度が速いので、なるべく長く地殻を通った方が、全体的な伝搬時間は短くなる。 無反射経路では、地殻からマントルに入射角90°で突入する場合が最も長く地殻を通ることになる。 マントル内部は、マントルを最短距離で伝搬するものとする。 尚、ここでは、理論的に超えられない最速値を求めることが目的であるので、単純に最速経路がどうなるかだけを考えればよく、地殻とマントルの境界面での屈折率を考慮する必要はない。 というのも、マントル内部で直進する限り、屈折率を考慮しても伝搬が速くなることはないからである(マントル内部で曲がって進む場合は後で別途考慮する)。 当然、マントルから地殻を出た後の経路は、入射時と対称の経路が最速となる。
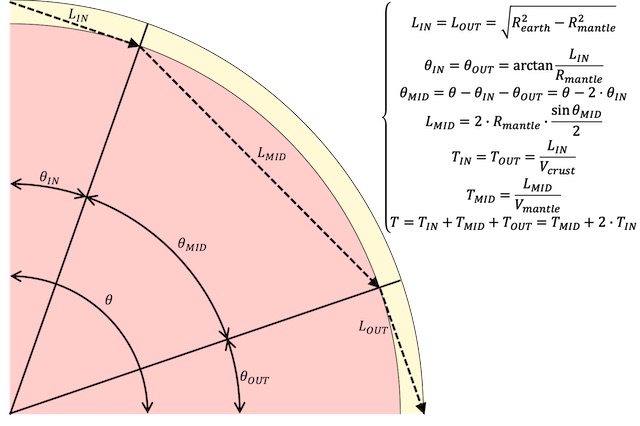
この場合の伝搬時間は、2×√{地球半径2-マントル半径2}÷【「地殻最下端部」の伝搬速度】+2×マントル半径× sin{(θ-θIN-θOUT)÷2}÷【マントルの伝搬速度】となる。 尚、θIN=θOUT=arctan[√{地球半径2-マントル半径2}/マントル半径]である。
そして、「地殻最下端部のP波の伝播速度を8km/s、マントル最上部でのP波の伝播速度を3km/s」と石田昭氏が採用した値を用いて、理論上の走時曲線と実測値を比較する。
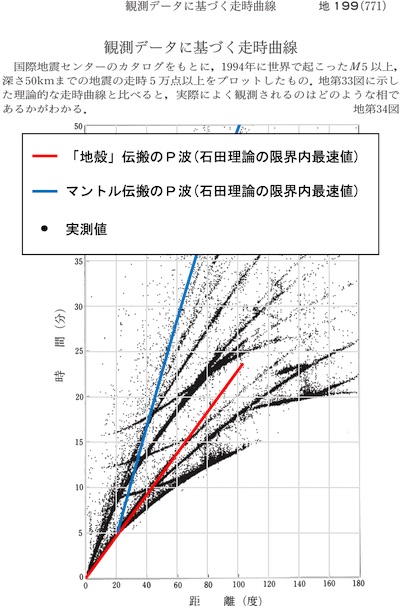
赤い線は、地殻内を伝搬するP波の理論上の走時曲線である。 青い線は、マントル内を伝搬するP波の理論上の走時曲線である。 赤い線は、30°以内では実測値と大差ないが、距離が遠くなるに従って実測値よりも遅くなり、最大で10分近く遅れる。 青い線は、実測値よりも圧倒的に遅い。 先ほども説明したとおり、いずれも、伝搬時間の理論上の最速到達値を採用している。 それなのに、計算の方が実測よりも到達が遅いということは、「地殻の厚さが100kmと仮定し、地殻最下端部のP波の伝播速度を8km/s、マントル最上部でのP波の伝播速度を3km/s」でP波が「二層構造の地殻内部を屈折と反射を繰り返しながら、伝播している」とする仮定と実測が全く一致していないことを意味する。
次に、マントル内を伝搬するP波の伝搬速度を8km/sとして同様の計算を行うと次の通りとなる。
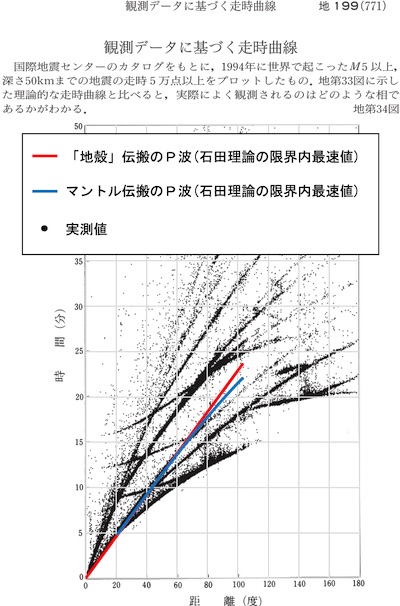
これでもまだ、理論上の波の到達が、実測値よりも圧倒的に遅い。 マントル内を伝搬するP波の伝搬速度を「地殻最下端部」のそれより速くすれば、P波の到達を速めることは可能である。 例えば、マントル内を伝搬するP波の伝搬速度を15km/sにすれば、理論値が実測値に追いつく。 しかし、マントル内を伝搬するP波の伝搬速度を「地殻最下端部」のそれより速くするということは、マントルの剛性率が「地殻最下端部」のそれより高くなることを意味する。 つまり、その場合は、固体である「地殻最下端部」より剛性率が高い以上、マントルも固体でしかあり得ない。 マントルが液体であるためには、当然、【マントルの剛性率】<【「地殻最下端部」の剛性率】であり、すなわち、【マントルの伝搬速度】<【「地殻最下端部」の伝搬速度】でなければならないが、その場合は、理論値が実測値より10分近く遅れることになる。 だから、理論値が実測値に追いつくためには、【マントルの剛性率】>【「地殻最下端部」の剛性率】でなければならない。 つまり、マントル熔解論では、どうやっても、理論値と実測値が一致しない。
実は、「マントル最上部でのP波の伝播速度を3km/s」とし、地殻とマントルの境界で内向きに屈折した後、マントル内部で外向きに屈折(カーブ)する経路を想定すると、マントル内を直線経路で「伝播速度を3km/s」で通過するよりも速い。
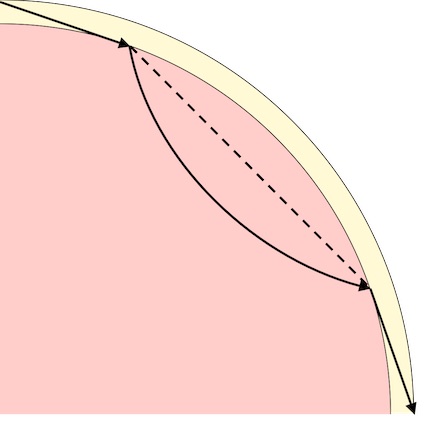
しかし、マントル内部で外向きに屈折(カーブ)するためには、マントルの内側ほど伝搬速度が速くなければならない。 そして、屈折(カーブ)する経路は直線経路よりも長くなるため、実測値に追いつくためには、マントル内部の平均伝搬速度は先ほど示した15km/sより速くなければならない。 その場合、伝搬速度に対応する剛性率から、表面を除く大部分のマントルは固体でなければならない。
マントル内部の平均伝搬速度が「地殻最下端部」の伝搬速度を上回るなら、地殻を通る距離が短い方が、全体的な伝搬時間は短くなる。 仮に、地殻を通る距離をゼロと仮定すると、実測値に追いつくためには、マントル内部の平均伝搬速度は11.5km/sより速くなければならない。 この場合、多少、液体部分を増やせるが、それでも、大部分のマントルは固体という結論には変わりない。
さらに言えば、先ほどの石田昭氏のシャドーゾーンの理論を適用すると、「143度」まではマントルを通過したP波が到達することはないから、グラフの赤い線でしかP波は到達し得ないことになる。 そのため、マントル熔解論では、遠くなるほど、走時曲線の計算値と実測値が一致しなくなる。 走時曲線の計算値と実測値が一致するためには、マントルを通過したP波が「143度」より内側に到達する必要があり、その場合はシャドーゾーンが全く説明できなくなる。
これに対して、石田昭氏は、実測値は「理論値に合致するものだけを『恣意的に』認定した結果」だから信用ならないと主張するかもしれない。 しかし、ここでは、最も早く届くP波の到達時間を比較しているため、「理論値に合致するものだけを『恣意的に』認定」するような細工は不可能である。
以上の通り、走時曲線の実測値は、マントルが固体でないと説明できない。
また、地震爆発論を否定する方の中には、様々な反論を書いて、爆発論を笑う方もあります。
また、地震波の走時曲線の問題があります。 地震爆発論では地震波の高周波成分の挙動として走時曲線は成立していると考えています。 つまり走時曲線が完全な間違いだとは言っていません。 ただし、高周波成分以外の主要震動成分の波動は走時曲線(表)のようには挙動していないと考えています。 ([1464]、{1553]など参照)
震動被害を起こすような主要震動は液体であるマントル内部を伝播するのではなく、固体である地殻内部を反射・屈折しながら伝播していると考えています。 だから、実測値(高周波成分の波動)よりははるかに遅いのです。 ([2339]レオロジーに関する地球物理学者の間違い解釈参照)
石田昭氏の主張があまりにデタラメ過ぎて何処から突っ込むべきかわからない(笑)。
まず、反論する意志があるなら、定性的な妄想論を述べるのではなく、石田理論での計算値と実測値が合致することを示すべきである。 当ページでは、既に、石田理論に基づいた理論上の最速値が実測値に全く追いつかないことを定量的に示している。 だから、石田昭氏が妄想に基づいて「定性的にはこうなるはずだ」と主張しても、全く反論になっていない。
石田昭氏が「走時曲線が」「間違いだとは言って」るかどうかは、ここでは全く関係がない。 石田昭氏が何と言おうが、石田昭氏の妄想が現実となるわけではなく、実測された値こそが現実である。 そして、理論値と実測値に差が生じる正当な理由が説明できないなら、理論値を疑うべきであることは言うまでもない。 石田理論と実測値が合わないこと、および、両者の差が出る理由を石田昭氏が説明できないことが全てなのである。 石田昭氏が実測値を「成立している」と認めるかどうか、「間違いだと」主張するかどうかは、物事の真偽とは全く関係がない。
地震波の伝搬特性として「走時曲線(表)のよう」な実測値が得られていることは疑う余地のない事実である。 それは、いくら、石田昭氏が「走時曲線(表)のようには挙動していない」はずだと主張しても、捻じ曲げることができない客観的事実なのである。 だから、「固体である地殻内部を反射・屈折しながら伝播している」とする理論が「実測値」「よりははるかに遅い」ことが決定的な反証になるのである。 「実測値」と同等の時間で実測される何かが到達するよう修正あるいは補正できれば、反証に耐えられる理論となり得る。 しかし、何の根拠も示さずに実測値を否定しても、そのような言説には何の意味もない。
石田昭氏は、波の伝達の基本的なメカニズムを理解していない。 「片栗粉を水で練った状態にすると」「短い周期で飛び跳ねれば、沈むことなく歩ける」とやらが事実だとしても、それは縦波(P波)の性質を説明できても横波(S波)を説明できることにはならない。 それは、力を加えた方向へ抵抗であり、力を加えた方向への強い圧力を伝えるものだから、縦波(P波)の性質を説明できる。 しかし、力を加えた方向の横方向に圧力を伝達できなければ、横波(S波)を説明できることにはならない。 横波(S波)を伝える上で重要な要素は分子同士の結びつきである。 個体のように分子同士の結びつきが強いと、力を加えた方向の横方向にある分子も釣られて動く。 横方向の分子のさらに横の分子も釣られて動き、さらに横の分子も…という風に横波(S波)は伝わっていく。 分子同士の結びつきが全くないと、力を加えた方向の横方向にある分子が釣られて動くことはないから、横波(S波)が伝わることはない。 分子同士の結びつきが弱いと、力を加えた方向の横方向にある分子が少し釣られるが、釣られる度合が小さいので、横波(S波)の伝搬速度は遅いし、減衰しやすい。 以上の通り、横波(S波)の伝搬特性は、力を加えた方向の横方向にある分子がどれだけ釣られるかで決まるのであり、「短周期振動」か「低周波振動」かは関係ない。
石田昭氏は、「短周期振動」は「低周波振動」より速く伝わると主張したいのだろうが、それでも、液体と固体の速度が逆転することはあり得ない。 何故なら、石田昭氏が主張するような液体が固体のように振る舞うことを認めたとしても、液体が固体よりも剛性が高くなることはあり得ないからである。 液体が固体よりも剛性が高くならない以上、波の伝搬速度の物理公式により、液体と固体の速度が逆転することはあり得ない。 よって、マントル内部の波の伝搬速度が想定より速かったとしても、マントルが熔解している限り、次の図が理論的限界となる。

「固体である地殻内部を反射・屈折しながら伝播している」速度が想定より速かったとしても、マントルが熔解している限り、次の図が理論的限界となる。
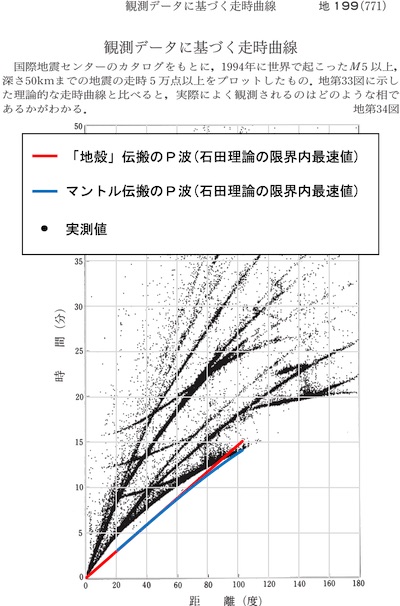
この場合、100°近辺では実測値と理論値が一致するが、逆に、実測値が数分遅れる領域が生じてしまう。 いずれにせよ、マントルが熔解している限り、「固体である地殻内部を反射・屈折しながら伝播している」速度が最速で伝わることになる。 しかし、そのマントル熔解論で最速の波が実測値に一致しないのだから、マントル熔解論は実測値と辻褄が合っていないのである。 そして、「固体である地殻内部を反射・屈折しながら伝播している」速度が最速の場合、伝搬時間は距離に正比例するので、走時曲線は必ず直線となり、次のようなカーブを描くことはない。
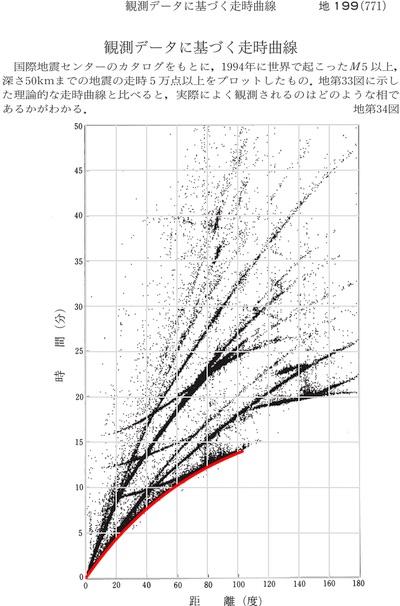
走時がこの図のようなカーブを描くためには、次の双方の条件を満足しなければならない。
- 「地殻内部を反射・屈折しながら伝播している」波よりも短距離のショートカット経路を通る波の方が早く到達する
- マントルの奥深くに行くほど伝搬速度が速く(剛性が高く)なる。
伝搬時間は距離に正比例しないためには、前者の条件は必須である。 しかし、マントル熔解論ではこの条件を満足し得ないので、理論値と実測値が一致することはない。 また、カーブの曲率を説明するには、前者だけでは不十分であり、距離が長いほど平均伝搬速度が速くなる必要がある。 そのためには、マントルの奥深くに行くほど伝搬速度が速く(剛性が高く)なる必要がある。
尚、浅発地震と深発地震の違いは、石田昭氏による情報歪曲等で説明した通り、「一箇所での波形記録を見ているから」からではなく、存在する波形を石田昭氏が隠しているだけである。 浅発地震で強震動が生じるタイミングに相当する時刻に達する所まで、深発地震の波形を示していないから、その部分を見ることができないだけに過ぎない。 そのようなインチキな比較から考察をすることは科学的には全くの無意味である。
「参考:(節操のないサイト「反証」より)」と書いてあるから、ここを読んで主張しているはずなのに、ここに書いてあることに一切反論しないで、結論を断定形でゴリ押しするだけとは呆れ返る他ない。 敢えてリンクを貼らなかったのは、「反証」を見られては困るからなのだろう。 つまり、石田昭氏は、何ら反論をしていないことを自覚しているのだ。
距離減衰率の理論値と実測値が合わない
「殆どのエネルギーは二層構造の地殻内部を屈折と反射を繰り返しながら、伝播している」理論では、主流学説と比べて、近場で震度が大きくなる一方で、距離による減衰が大きくなる。 とくに、地表での反射は、建造物の破壊等によりエネルギーを消費する分だけ、地震波の振幅を小さくする。 また、遠方では、主流学説より遠回りをするため、減衰が激しくなる。 観測結果と主流学説の矛盾は指摘されておらず、主流学説より距離減衰率が大きいのでは観測結果と合わない可能性が高い。
深発地震で地震爆発論(笑)の地震発生原理が成立しない
石田昭氏による情報歪曲等で紹介した通り、石田昭氏は主流学説と深発地震の辻褄が合わないと主張する。 しかし、深発地震と辻褄が合わないのは地震爆発論(笑)の方である。
石田昭氏の化学や物理の法則に対する無理解で紹介したとおり、地震爆発論(笑)では、「マグマオーシャンといわれる熔融マグマの海であった」「原始の地球」のうちの「地球表面のマグマ」のみ「が冷却され」、「地殻の下部、地球内部はマグマオーシャンのまま」であるとする。 それならば、少なくともマントル内では、次のような地震爆発論(笑)の地震発生原理が成立しない。
- 爆鳴気が「地下水がマグマの高熱に接して起きる熱解離という作用で発生」
- 「爆鳴気と言われる解離ガスであってもすぐには爆発し」ない温度まで「周囲の温度はいったん降下」
- 再び、マグマの熱で着火して水素爆発が発生
- 以下略
2番目の過程は「マグマオーシャンのまま」の高温領域では絶対に発生し得ない。 よって、マントル熔解論では、地震爆発論(笑)の地震発生原理に基づいた深発地震が発生し得ない。 言い換えると、深発地震の存在こそが、地震爆発論(笑)の地震発生原理とマントル熔解論が両立しないことの極めて明確な証拠である。
このページへのご意見は節操のないBBSにどうぞ。
総合案内
科学一般
疑似科学等
- 疑似科学
- 数学や科学への無理解
- 疑似科学を批判する疑似科学
- STAP細胞論文捏造事件
- CCS地震原因説
- 地球温暖化懐疑論
- 疑似科学者列伝