二重スリット実験の真相

素人でも直感的に理解できるよう、かつ、科学的に正しく二重スリット実験を説明する
前置き
- 科学で扱える現象の範囲
- オッカムの剃刀
実験と結果
実験結果から直接分かること
科学的考察
過程を検証する試み
誤った説明の例

素人でも直感的に理解できるよう、かつ、科学的に正しく二重スリット実験を説明する

ネット上には、二重スリット実験について、トンデモな疑似科学的情報が氾濫している。素人が読んで内容を理解できるものは、ほぼ全て、トンデモな疑似科学的な説明となっている。一方で、真っ当な説明が行われているものは、素人が読んでも理解不可能なくらいに難解である。そこで、素人でも直感的に理解できるよう、かつ、科学的に正しく二重スリット実験を説明することとする。

尚、素人にも直感的に理解できるよう二重スリット実験を説明するが、嘘をついてまで分かりやすく説明をするつもりはない。何故なら、嘘の説明では、丸め込まれているだけで、分かったうちに入らないからである。もちろん、ここでは、重要部分では一切嘘をつかないが、細部の不正確さは許容している。「もっと分かりやすい説明がある」と言う人もいるかもしれないが、その殆どは根本的に説明が誤っている。つまり、その「もっと分かりやすい説明」とやらは、理解を促進しているのではなく、信じやすい嘘を教えているだけなのである。

期待した結論を導いたかどうかで分かりやすさを評価しているなら、それは次の理由で全くの見当違いである。二重スリット実験は、世界で初めて、単位量でも波動性と粒子性が両立することを証明した実験である。この実験からそれ以上のことが分かるとする説明は全て嘘である。実験から判明する結論が限定しているのだから、どんなに分かりやすい説明をしても、それ以外の結論を引き出すことはできない。分かりやすいとは、詭弁を用いて聞き手を無理やり納得させることではなく、正しい事実を正確かつ最大限に聞き手に伝えることである。動画で手っ取り早く見たい方はYouTubeへどうぞ。

【真】本当の二重スリット実験 - YouTube

量子力学には古典力学の範囲に収まらない不可思議な現象があるが、二重スリット実験の結果だけで良ければ古典力学の範囲で十分に説明可能である。 粒子性と波動性が両立するだけなら、古典力学の範囲で十分に説明可能なのだ。確かに、粒子性と波動性の両立は、古典力学の範囲に収まらない現象の構成要件ではある。隠れた変数理論の一種である量子ポテンシャル理論も古典力学の範囲を超えている。しかし、古典力学の範囲に収まらない現象を生じさせるには、ベルの不等式の検証実験等が必要であり、粒子性と波動性の両立だけでは圧倒的に足りない。にもかかわらず、二重スリット実験の結果が古典力学で説明不可能なように解説しているなら、それは科学的に誤ったトンデモ解説である。

二重スリット実験が古典力学で説明不可能な不可思議さを示していると主張する者は、論理的思考や科学的思考に反しているばかりか、容易に説明可能なことまで無駄に難しくする独自理論で二重スリット実験の説明を試みている。その結果、二重スリット実験は古典力学の範囲では説明不可能な不可思議な現象だと主張する。しかし、それが不可思議なのは、二重スリット実験の方ではなく、その人の思考の方であろう。

量子力学の説明を十分にした上で、量子力学の不可思議さの構成要件として粒子性と波動性の両立を説明することには意味がある。しかし、二重スリット実験を古典力学の範囲では説明不可能な不可思議な現象として紹介することは科学的に明らかに間違った説明であるし、最初にそうした説明をすると余計な混乱を生むだけである。古典力学の範囲に収まらない不可思議なことを説明するために二重スリット実験を持ち出すのは明らかに不適切であり、そうした説明をしたいなら別の実験等を用いるべきである。そのことに気づかない者は量子力学を全くわかっていないと言える。尚、ノーベル物理学賞を受賞した朝永振一郎氏による光子の裁判も、科学的には間違っていないが、粒子性と波動性を混同した説明により疑似科学的誤解を産む一端を担っている。

尚、トンデモ理論でよく採用されている説明手順における科学的に正しい説明は二重スリット実験(疑似科学からの脱洗脳)に示す。

前置き

当サイトの科学項目の目的も参照のこと。

科学で扱える現象の範囲

科学で扱うためには、同じ条件では同じ現象になる(同じ数式で記述できる)ことが必須の前提となる。 その前提が崩れれば、科学法則が成立しないし、実験の再現性も失われる。よって、科学法則を見出したり、実験で結果を確かめるためには、この前提が崩れてはならない。言い換えると、同じ現象にならない(同じ数式で記述できない)ケースを科学で扱うためには両者には違う条件が必要となる。尚、量子力学は確率的に結果を推定する理論であるので、ここで言う「現象」には確率も含む。

オッカムの剃刀

実験結果を説明するために不要な仮定は置かない。必要のない仮定を置いても、理論的考察の役にたたない。無駄に話を難しくすれば、間違いを生みやすくなる。メリットが全くなく、かつ、デメリットしかない不要な仮定は可能な限り排除すべきだろう。

実験と結果

ヤングの実験

一度別れた後に再び合流するような経路を設け、そこに位相の揃った波を通すと干渉縞が発生する。トーマス・ヤングは、波のこの性質を利用し、２つのスリットを用いた干渉実験で光が波であることを示した。

電子の二重スリット実験

光子も電子も、それ以上分割できない最小単位を持つ。

量子力学では、光子も電子も、波としての性質を持つとされる。

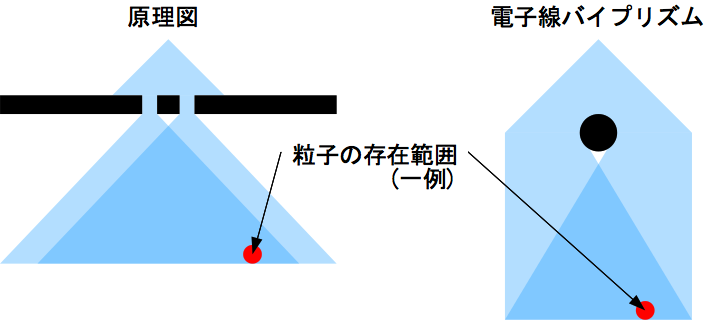
電子の波としての性質を確認するためにヤングの実験と同様の二重スリット実験が考案された。ただし、実際の実験では「スリット」ではなく電子線バイプリズムが用いられた。

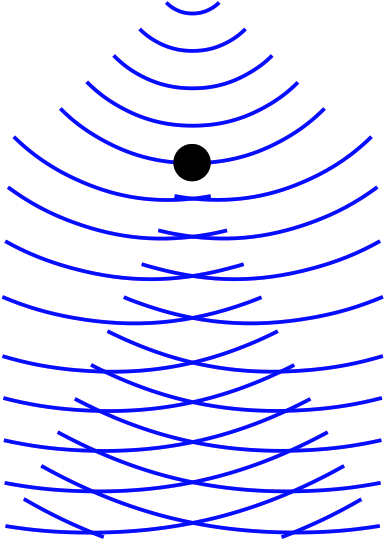
これは、１ミクロンの金属糸で左右の経路を分断したものであり、金属糸がプラスに荷電してマイナス荷電の粒子の軌道を中央寄りに曲げる働きがある。原理的な装置では、２つの電子の経路を交錯させるためにスリットにおける波の回折現象による広がりを利用する。しかし、この装置では、スリット通過前からある程度の幅がある２つの電子の経路をクーロン力で交錯させているため、必ずしもスリットにおける回折による広がりは必要がない。

たとえば重力下での粒子(図ではボールにしてある)の運動を考えると、高いところほど位置エネルギーmghが大きいから、その分物質波の波長が長くなる(運動エネルギーが減る)。この場合はポテンシャルは連続的に変化していくが、図のように段階的に変化していくとしよう(図で書いた点線の境界面を上に超えるごとにmgΔhずつポテンシャルが高くなるとする)。

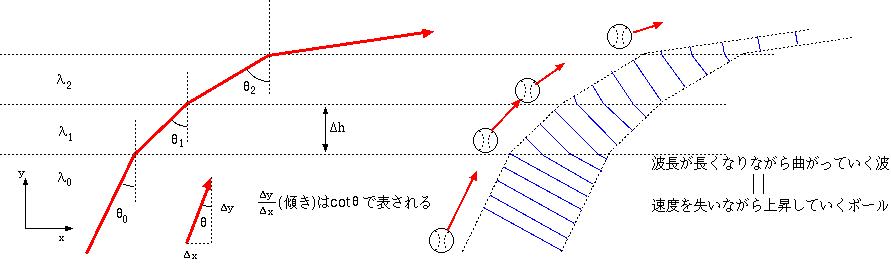
境界線を上に超えるごとに波長が長くなっていくから、そのたび、波が下に下にと曲げられていく。上の問題を解くとわかるように、これは重力場中で投げ上げられた物体が落下するという現象だと解釈できる。古典力学でも波動力学でも運動方程式が出てくるのだが、古典力学では力によって運動量が変化すると説明し、波動力学では波長の差が波を曲げる、と説明するのである。
初等量子力学講義録2005年第７回 - 琉球大学理学部物質地球科学科准教授前野昌弘の講義録

電子１個分相当の量を射出し、スクリーンへの着弾を確認する。確認した後、また、電子１個分相当の量を射出する。これを、繰り返すと、毎回毎回、スクリーンには１個以下の輝点が発生する。１個以下となるのは、スクリーンへの着弾確率が１００％でないからである。そして、限りなく多数の射出を繰り返すと、輝点の集合体には一定の模様が現れる。この模様は、波の干渉縞に良く似ている。

光の二重スリット実験

光子でも１個分相当の量単位での干渉実験が行なわれている。

ヤングの実験で入射光を非常に弱くしてみる。
スクリーンには、薄い縞模様ではなく、点が現れる!
浜松ホトニクス中央研究所
初めて学ぶ物理学量子論 by 筑波大学物理学系素粒子理論研究室金谷和至教授

こちらは原理に忠実な方法であるので、スリットにおける波の回折現象による広がりを利用している。光子の場合も、輝点の集合体による干渉縞模様が発生している。

単一スリット実験

単一スリット実験では次のような結果が得られる。

二重スリット実験の片方のスリットを閉じた場合や干渉縞の必須条件を崩すと、干渉縞は生じないが、輝点は空間的な広がりを示す。

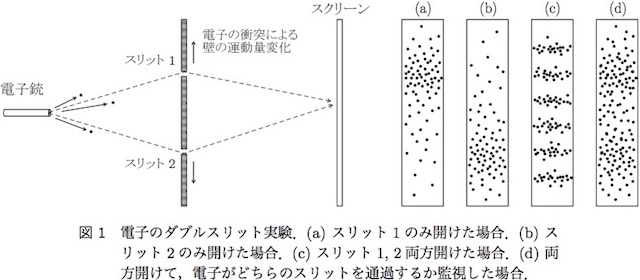
干渉と識別の相補性(谷村省吾) - 名古屋大学多自由度システム情報論講座

尚、この谷村教授の説明図は、一箇所、間違いではないが正確性を欠く部分がある。実際の二重スリット実験では、スリット間隔は非常に短く、スクリーンまでの距離の方が圧倒的に長い。例えば、電子線バイプリズムを用いた二重スリット実験では、スリット間隔は１μm以下、スクリーンまでの距離は1メートルであった。浜松ホトニクスの光子の二重スリット実験では、スリット間隔は50μm（スクリーンまでは数十cm？）であった。その結果、２つのスリットの強度のピーク位置はほとんど差が生じず、この絵で見るようにハッキリ分かれて見えることはない。遅延選択量子消しゴム実験や二重スリット量子消しゴム実験でもそのようになっている。おそらく、全てご存知の上で説明をわかりやすくするために必要な誇張をされたのだろう。

実験結果から直接分かること

結論

二重スリット実験が意味することは「単位量の光子や電子であっても波としての性質を示す」ということだけである。 波としての性質が現れるために複数の光子や電子を必要としないこと、すなわち、単位量の光子や電子であっても波としての性質を示すことを世界で初めて実証したのが二重スリット実験である。 二重スリット実験にはそれ以上の意味はない。

事実関係等の整理

この実験の結果から直接読み取れる事実を次に列挙する。

スクリーン上の模様は全て小さな輝点によって構成されている。【実験事実A】
各輝点は一定範囲に分布し、その密度による濃淡が干渉縞を形作っている。【実験事実B】
輝点は時間とともに増えるが、２個以上の輝点が同時に発生することはほぼない。【実験事実C】

以上の実験事実を踏まえないと頓珍漢な結論を導いてしまう。

時系列的考察

【実験事実B】から、この実験では、少なくともスクリーン着弾までは波としての性質を維持しなければならない。もしも、着弾前に波としての性質がなければ、次の様な結果（原理的装置、電子線バイプリズムの順）になるはずである。

しかし、実際の実験では、次の様な結果になっている。

原理的装置でパターンが横に広がっていること、および、両者の干渉縞は波としての性質がないと説明不可能である。よって、着弾前には波としての性質があると推定できる。

しかし、着弾以降については、波としての性質の有無には言及できない。というのも、波としての性質は【実験事実B】から間接的に推定されているのであって、波を直接観測することはできないからである。それは、着弾前も着弾以降も変わらない。すなわち、着弾前も着弾以降も波を直接観測することはできない。着弾前に波としての性質を持つことは【実験事実B】から推定可能だ。しかし、着弾以降は、そのような間接的な証拠がない。直接的にも間接的にも証拠がなければ、波としての性質を持つかどうかを検証することはできない。

【実験事実A】から、この実験では、少なくともスクリーン着弾後には粒子としての性質が現れていなければならない。もしも、着弾後に粒子としての性質がなければ、次の様な滑らかなグラデーションになるはずである。

実際の実験では、次の様な結果になっている。

このように、干渉縞は、着弾した粒子に対応する多数の点で構成されているので、測定するまでに、粒子としての性質が現れなければならない。

しかし、着弾前には測定をしていないので、粒子としての性質があるのかどうかはわからない。というのも、粒子としての性質は【実験事実A】から推定されているのであって、それは着弾後に得られる結果だからである。少なくとも、この実験では【実験事実A】を得ることができない着弾前の粒子性の有無は推定できない。

以上をまとめると次の表になる。

	測定前	測定後
波動性	あり(確定事項なので別の可能性を論じる必要なし)	不明(ある場合とない場合の両方を検討する必要あり)
粒子性	不明(ある場合とない場合の両方を検討する必要あり)	あり(確定事項なので別の可能性を論じる必要なし)

表で「不明」となっている部分は、隠れた変数理論の真偽によって変わるが、二重スリット実験では言及することができない。この実験が意味することは、光子や電子が、着弾までは波としての性質を持っていることと、着弾してから測定までの間に粒子としての性質が現れていることだけである。着弾後の波動性や着弾前の粒子性については、本実験から結論を導くことは出来ない。

波と粒子の二重性

量子力学における波動性と粒子性の二重性の意味を正しく理解できていないと、この実験の意義は理解できない。

粒子は一点に凝集して存在する
波は空間的な拡がりを持つ

この実験においても、【実験事実A】は一点に凝集した何かを示唆している。そして、【実験事実B】は空間的な拡がりを持つ何かを示唆している。しかし、空間的な拡がりを持つ性質と、一点に凝集して存在する性質の２つの性質を併せ持つことは非常に奇妙である。

クリントン・デイヴィソンらは、電子線の回折実験で電子に波としての性質があることを証明した。しかし、その波としての性質が最小単位の電子でも生じることまでは証明されていなかった。とはいえ、波動力学で原子モデルを説明するためには、最小単位の電子でも波としての性質が必要になる。また、最小単位の光子でも波の性質を示すと考えられていた。

問題は、波のような性質をもたらすほど光子の数は多くないことである。
つまり、ある一瞬には、室内の光子数は10の12乗個程度しかない。これは、１立方ミリメートル当たり10個程度ということであり、空気分子が10の16乗個程度であるのと大きな違いである。
「量子力学の解釈問題―実験が示唆する『多世界』の実在」(ISBN-10:4062576007,ISBN-13:978-4062576000,著:ColinBruce,訳＆注:和田純夫)P.35

空気分子の数と比べて論じるのは乱暴なので、もう少し補足説明する。「１立方ミリメートル当たり10個程度」を単純計算すると、光子と光子の平均間隔は0.46mmくらいであろうか。それに対して、可視光線で最も長い波長は約800nmである。以上により、この場合の光子と光子の平均間隔は波長の５７５倍となる。常識で考えれば、複数の粒子が波を形作るなら、粒子と粒子の平均間隔は波長よりかなり短くなければならないはずである。しかし、実際の光子と光子の平均間隔は波長の５００倍以上も開いている。これでは、複数の粒子が波を形作るとは考えにくい。

この実験では、【実験事実C】は波動性を示すために複数の粒子を必要としないことを示唆している。つまり、たった１個分相当の量の電子や光子であっても、粒子性と波動性を両立していることになる。 そうすると、電子や光子は、一点に凝集しつつも空間的な拡がりを持つという奇妙なことになってしまう。 それが如何に奇妙かは、波の分割を示す次の図を見てもらいたい。

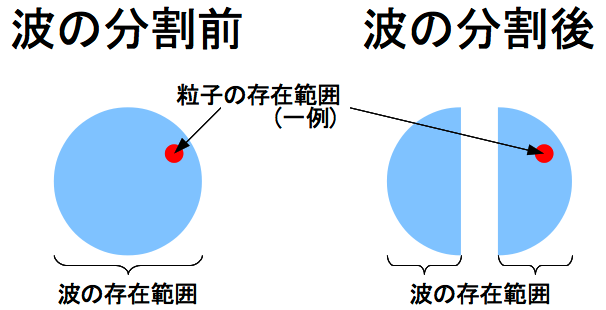
図を見て分かる通り、波が分割される前から、波と粒子の存在座標には不一致が見られる。これが不可思議であることは、波の分割の前後で変わりはない。ただし、分割後の不可思議さは多少増えている。分割前には、波の存在範囲に空間的連続性があり、かつ、波の存在範囲のいずれかに粒子が存在する。一方で、分割後には、波の存在範囲が不連続となり、分裂した波の一方には粒子が存在しない。不可思議さが増えていることは確かだが、不可思議さの増分は元からある不可思議さに比べれば大したことはない。何故なら、この不可思議さの本質は、波と粒子の空間的特性が一致しないことにあるのであり、それがなければ分割後の不可思議さも発生しないからである。

二重スリット実験の場合は、経路が二手に分かれていても、空間的に分断されているわけではないのだから、空間的には連続的な波となっているはずである。

このように考えると、経路が１つだろうが２つだろうが、不可思議さには変化がないと言える。また、波が２つの経路を通ることも何ら不可思議な現象ではない。空間的な広がりを持っているならば、その広がりの範囲にある限り、通れる経路を全て通ることは当然の帰結である。 本当に不可思議なことは、２つの経路を通ることではなく、２つの経路を通ることが可能なだけの広がりを持っていることなのである。 繰り返すが、粒子として１点に凝集される性質と、波として空間的な広がりを持つ性質を両立していることが不可思議なのである。

科学的考察

共通的考察

一見すると矛盾に見える波動性と粒子性の両立に対する一定の答えが、ボルンの確率規則である。そして、既に説明した通り、二重スリット実験では、次のいずれが正しいのかを確かめることができない。

着弾前にも粒子性がある
着弾前には粒子性がない

一般常識で考えれば、着弾前の粒子性がないと考えることには相当の無理があるように思える。 しかし、自著「量子力学の数学的基礎」にてノイマンは、ありとあらゆる量子力学的現象と辻褄の合う理論を構築しようとすると、着弾前の粒子性を認めることが数学的には非常に困難であることを指摘している。このノイマンの指摘には反論もあり、前提条件次第では、着弾前の粒子性を認める理論が構築可能であることがわかっている。しかし、ベルの不等式やコッヘン・シュペッカーの定理等により、着弾前の粒子性を認めるための前提条件が非常に厳しく、極めて歪な理論でしか実現できないことがわかってきた。 現在においても、着弾前の粒子性の有無については決着がついていないが、どちらか一方を強く支持するだけの科学的根拠は見出だされていない。

現在の標準理論は、ノイマンが提唱した数学的手法が採用されており、その計算過程では波動関数は空間上に広がって伝搬する。この波動関数の広がりは、粒子の多数の存在可能性の集合体を示しているとも言える。そして、波動関数は、測定した途端に急速に一点に収縮する。収縮現象は、存在可能性が一つだけを残して全て消滅することを示しているとも言える。この標準理論の計算結果があらゆる実験結果等と一致していることは実証されているが、その計算過程が実際の物理的現象を表現しているかどうかの科学的証拠はない。むしろ、二重スリット実験だけを見れば、標準理論は非常に馬鹿げているようにしか見えない。

以上を踏まえて、トンデモ論や疑似科学を除くと、大きく分けて３つの解釈がある。

途中の過程ではどうかは分からないが、測定結果は標準理論に従う（コペンハーゲン解釈）
標準理論における計算過程が実際の現象を指している
波と粒子の双方が同時に存在すると考え、具体的な粒子の軌道を想定する(二重解の理論とその派生理論)

主流派のいわゆるコペンハーゲン解釈では、この実験の過程については一切言及しない。もちろん、標準理論の計算方法には、計算過程が存在する。しかし、コペンハーゲン解釈では、これは、結果を計算するためのツールに過ぎないとして、計算過程の物理的意味を考えない。

現実の現象との関連性については諸説あり、標準理論の計算過程が現実の現象を表していると解釈する者もいる。多世界解釈によれば、収縮現象は、分岐後の世界の一つのみを知覚できることによって生じる、見かけの現象とされる。

隠れた変数理論の一種である二重解の理論とその派生理論では、波と粒子の双方が同時に常に存在すると考え、具体的な粒子の軌道を想定する。もちろん、これらの理論も標準理論と数学的に等価な理論である。例えば、量子ポテンシャル理論では、二重スリット実験の粒子軌道は次の図のいずれかのような軌道を取る。

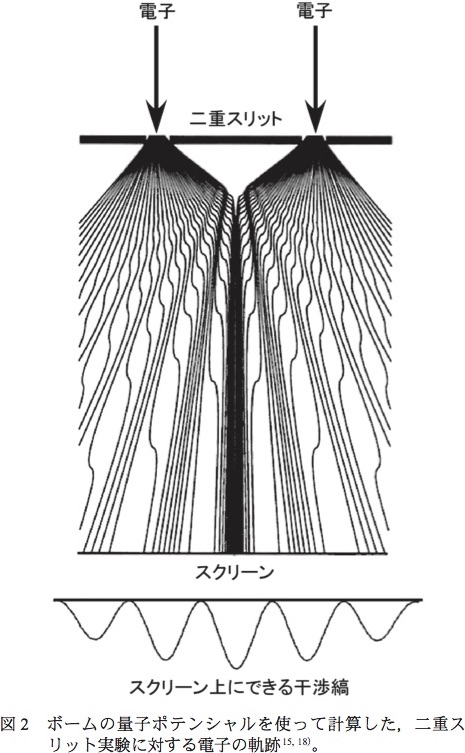
波動関数のわかりやすい説明(林久史) - 日本女子大学理学部物質生物科学科

この図のうちのどの軌道を取るかは粒子の初期位置で決まる。引用元の引用文献は次の通り。

D. Bohm, B.J. Hiley: The Undivided Universe, Routledge, London(1995).
D. Dürr, S. Teufel: Bohmian Mechanics The Physics and Mathematics of Quantum Theory, Springer, New York(2009).

エドワード・ネルソンの確率力学でも二重スリット実験の粒子軌道が計算できる。

これらのいずれが正しいのか白黒つけようとする研究は多々あるが、二重スリット実験はどちらが正しいのか検証できない。

隠れた変数理論との関係

通俗説では二重スリット実験が隠れた変数理論を否定しているかのような誤った説明が為されるが、二重スリット実験では隠れた変数理論を否定することはできない。 事実、隠れた変数理論の一種である二重解の理論とその派生理論でこの実験が矛盾なく説明できることは既に示した通りである。

隠れた変数理論では、粒子は同時に１つの経路しか通らないが、波は同時に複数の経路を通る。だから、２つのスリットが開いていれば干渉縞が生じるが、片方のスリットを塞ぐと干渉縞は生じない。正確に言えば、量子ポテンシャル理論では、波は量子ポテンシャルによる見かけの現象である。スリットが開いている数により量子ポテンシャルが変わり、それが粒子の軌道と見かけ上の波を変える。

このように、二重スリット実験の持つ量子力学的意義を正しく理解できていれば、それを隠れた変数理論の否定と絡めて説明する意味がないことを理解できる。正しく理解できていれば、二重スリット実験が隠れた変数理論を肯定も否定もしないことの説明として、隠れた変数でも説明可能なことに言及する必要性は感じるかもしれない。実際に、隠れた変数理論で説明可能なことを示した文献も複数ある。しかし、正しく理解できていれば、隠れた変数理論を否定した考察に言及する必要が全くないことに気がつく。言い換えると、正しく理解できていないからこそ、隠れた変数理論を否定した考察を披露しようとするのであり、その説明が量子力学の標準理論に適合しないのは当然のことと言える。

もちろん、隠れた変数理論を否定すると、二重スリット実験を考察した場合「も」(「は」ではない)、常識では考えれらない結論を導く。しかし、次のことに注意が必要である。

常識はずれは二重スリット実験に限らずに量子力学全般に当てはまる
二重スリット実験は隠れた変数理論を肯定も否定もしない(隠れた変数理論の真偽の証明には使えない)
隠れた変数理論の否定と二重スリット実験を絡めた説明のほぼ全てが量子力学の標準理論に全く適合しない

測定と波の性質の関係

標準理論の計算では、測定後は、射影仮説に基づく波動関数の収縮が起きる。しかし、それにより測定前の波としての性質がなかったことになるわけではない。二重スリット実験の干渉縞が、その良い証拠である。

John Archibald Wheelerが提唱したJ.Wheelerの遅延選択実験にて、粒子として測定しようとすると波の性質が失われるかどうかの確認が行なわれた。その結果、少なくとも、経路が別れた（スリットを通過した）直後には、波の性質が失われていないことが現実の実験結果として確認されている。遅延選択量子消しゴム実験の結果も、経路を特定できる場合にも波動性が失われていないことを示唆している。

「１つの粒子が２つの経路を同時に通過した証拠だ！」と明らかに頓珍漢な解釈をする人もいる。しかし、二重スリット実験(疑似科学からの脱洗脳)で解説する通り、「１つの粒子が２つの経路を同時に通過した」としても、それだけでは干渉縞の生成を全く説明できないことは言うまでもない。

また、干渉縞が生じないケースでは波動性が失われたと勘違いする人もよく見かける。しかし、ある命題が真であることは、対偶も真であることを保証するが、裏や逆が真であることを保証しない。

元の命題: 「干渉縞が生じれば波動性がある」＝真
対偶: 「波動性がなければ干渉縞は生じない」＝真
裏: 「干渉縞が生じなければ波動性はない」＝以下で検証
逆: 「波動性があれば干渉縞が生じる」＝以下で検証

これは論理学の基礎である。裏が真であるかどうかを知るには、元の命題ではなく、裏や逆(裏と逆はお互いに対偶関係になっている)を検証しなければならない。では、裏「干渉縞が生じなければ波動性はない」は成立するか。干渉縞が生じるためには、次の全ての条件を満足しなければならない。

波動性がある
スクリーンの位置に応じて経路差が変化する
双方の波の偏波(偏光)が揃っている
スクリーンの位置と経路間位相差が一対一で対応している
- 実験セットの位置関係が安定している
- 波の波長が安定している
- 波の位相が安定している(単一粒子射出の場合は経路分岐後に限る)
実験セットのスケールが適切に設定されている

これらの条件が１つでも崩れると干渉縞は生じない。つまり、波動性があっても、他の条件が１つでも崩れると干渉縞は生じない。波動性があっても干渉縞が生じないケース、言い換えると、干渉縞が生じないのに波動性があるケースが存在するなら、干渉縞が生じないことは波動性がない証拠とならないことは明らかだろう。

過程を検証する試み

まず、どのような前提で何の通過スリットを調べるのか整理しておく必要がある。二重スリット実験では、波の通過スリットを特定する意味はない。何故なら、波が一方のスリットしか通過しないなら、二重スリット実験の条件を満足せず、当然のごとく干渉縞が生じないからである。実験の過程を検証したいなら、実験の前提を維持しながら、通過スリットを特定しなければ意味がない。常識で考えれば、次の２つが両立しないことは明らかだろう。

波が二つのスリットを通る(二重スリット実験の条件を満足する)
波がどちらか一方だけのスリットを通ったことを示す測定結果が出る
- その測定結果は正しい

もちろん、測定結果が正しくなければ、何の矛盾も生じない。しかし、測定結果が正しいなら、その測定結果と前提事実に致命的な食い違いが生じる。前提と結果が矛盾するのだから、そのようなことはあり得ないと背理法で証明される。だから、二重スリット実験で通過スリットを特定すべきなのは波ではなく粒子である。 二重スリット実験の条件を維持する限り、波の通過スリットを特定できるわけがない。 二重スリット実験で特定可能なのは粒子の通過スリットだけである。 この整理がきちんとできていないと頓珍漢なことになる。実のところ、通過スリットを調べようとする試みの多くは波の通過スリットを調べようとしている。それは、今説明した通り、議論するまでもなく明らかに不可能である。

ここで次の２つの理論に大別する。

波の空間座標と粒子の空間座標は一致する(粒子は波が一点に凝集したものである)
波の空間座標と粒子の空間座標は必ずしも一致しない(ただし、粒子は波の存在範囲内にのみ存在し得る)

前者の理論においては、粒子の通過スリットと波の通過スリットは同一のものである。その場合、波の通過スリットが特定できなければ、粒子の通過スリットを特定できない。言い換えると、粒子の通過スリットを特定できるならば、波の通過スリットも特定できることになる。波の通過スリットを特定できるということは、波がどちらか一方のスリットしか通らないことになる。つまり、前者の理論においては、波が両方のスリットを通るという二重スリット実験の前提が崩れてしまう。二重スリット実験の前提が崩れるのでは、二重スリット実験の前提を維持したまま粒子の通過スリットを特定することは原理的に不可能である。

通過スリットを調べる意味があるとすれば、後者の理論における粒子の通過スリットを調べることだけである。言い換えると、通過スリットを調べる試みは、後者の可能性を実験で確かめようとする試みでもある。しかし、その確認に成功した事例は１つもない。それは、粒子の通過経路と干渉縞を同時に得ることはできない(相補性)という相補性原理が量子力学の根源的原理であるからだと考えられている。

ファインマンの思考実験

ハイゼンベルクは、位置と運動量を同時に特定できず、両者の曖昧さの積は常に一定値を上回るとする不確定性原理を提唱した。不確定性原理は、当初は、測定による擾乱として説明された。例えば、光を電子にぶつけて反射を測定して、位置を特定するとする。その光は、検出対象の電子の運動量を変化させる。電子の位置を正確に測定するには、より波長の短い光を用いる必要があるが、波長の短い光は運動量も大きい。結果、電子の位置を正確に測定しようとすると、電子の運動量を大きく乱す。電子の運動量を乱さない様に波長の長い光を用いると、電子の位置を正確に測定できない。結果、電子の位置と運動量の正確さは両立できない。現在は、測定による擾乱がなくても、不確定性原理が成立するものと考えられている。

不確定性原理を踏まえて、ファインマンは自著「ファインマン物理学Ⅴ量子力学」にて、二重スリット実験で粒子がどちらを通ったかを測定する次のような思考実験を紹介した。電子の二重スリット実験において、光を電子にぶつけて反射を測定して、スリット通過を判別するとする。その光は、検出対象の電子の運動量を変化させる。運動量と波長の関係式から、運動量が変化すれば波長も変化する。その変化量は不可逆かつランダムであるので、検出対象の電子の波長が一定ではなくなる。

通過スリットを判別可能にするには、スリット間隔よりも位置検出精度を高くする必要がある。そして、実験のスリット間隔が非常に狭いので、求められる位置検出精度は非常に高くなる。位置検出精度を上げれば上げるほど、不確定性原理により、電子の波長の標準偏差も大きくなる。通過スリットを特定可能な高い位置検出精度を求めると、検出対象の電子の波長の標準偏差が干渉縞を維持できないほど大きくなる。結果、通過スリットの特定と干渉縞は両立できない。

電子線バイプリズムを用いた実験では…

しかし、電子線バイプリズムを用いた実験であれば、不確定性(相補性)原理の影響を受けずに、通過スリットを特定できるのではないか。電子線バイプリズムを用いた実験では、金属ワイヤーで区切られた領域のいずれを通過したかを特定すれば十分であり、個々の領域の何処を通過したかまでは特定する必要はない。であれば、位置を曖昧にしたままの通過領域特定が可能であり、運動量に致命的な影響を与えることがないのではないか。

例えば、次の様な方法ではどうか。金属ワイヤーを１μｍ厚かつ数ｃｍ幅の金属板に置き換え、電子の飛行方向と平行となるよう設置する。そして、経路の片方に運動量に致命的な影響を与えない波長の長い光源を用意し、反対の経路からは金属板に遮られて光源からの光が到達しない様に光源の指向性を調整する。ここで、電子に反射した光をセンサーで検出すれば、電子の場所を正確に特定することはできないが、少なくとも、光源のある側を通過したことは特定できるはずである。同様に反対側にも光源とセンサーを設置すれば、双方の経路通過を特定できる様になるはずである。これらのセンサーでの検出と一致する結果のみを抽出すれば、経路を特定しながら干渉縞を得ることが可能ではないだろうか。

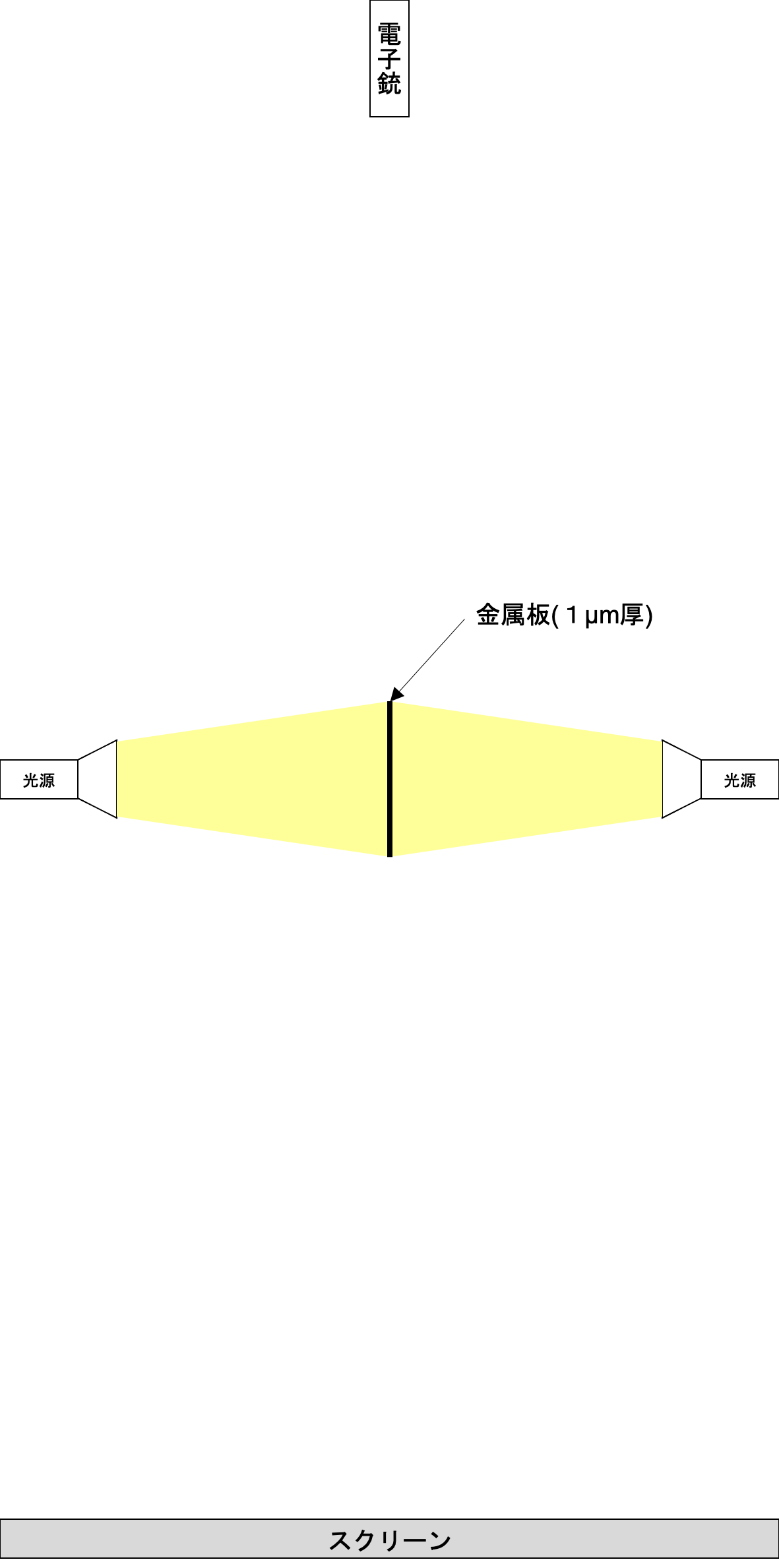
もしも、こうした実験により経路情報と干渉縞が両立できることが証明できれば、過程における可観測量が必ずしも不定ではないことを示すことができる。つまり、過程においては、正確な位置が確定しているとまでは断言できないが、少なくとも、二者択一の経路情報が確定しているかどうかは検証可能となる。隠れた変数理論が正しくないならば、位置は波が広がっている範囲全ての自由度を持つはずである。しかし、もしも、経路情報と干渉縞が両立できるならば、位置の自由度は波が広がっている範囲の半分に制限されてしまう。だから、経路情報と干渉縞が両立できれば、隠れた変数理論に極めて有利な証拠となろう。

反跳運動量

二重スリット実験を巡るアインシュタイン／ボーア論争を分かりやすく要約すると、アインシュタインは着弾点と反跳運動量（通過した粒子から受ける作用によるスリットの運動量変化）が分かれば粒子の通過した経路が分かると主張し、ボーアは次のように反論した。

反跳運動量を測定するためには、スリットの運動量の不確定性を小さくしないといけない
干渉縞の発生位置はスリットの位置によって決まるから、干渉縞を作るにはスリットの位置の不確定性を小さくしないといけない
不確定性原理により、スリットの運動量の不確定性を小さくすると位置の不確定性が大きくなる

これは、反跳運動量を測定しようとすると、スリットの位置が不確定になり、その結果、波の位相関係も不確定となるから干渉縞がぼやけるという話である。言い替えると、反跳運動量も不確定性原理の壁に阻まれるということである。

片側検出器

片方の経路にだけ検出器を置けば粒子の通った経路が分かるし、干渉縞も半分残るはずだ、とする主張がある。しかし、検出器を置いていない側の経路に影響しないことをもってして、干渉縞が半分残ると考えるのは明らかな間違いである。干渉縞は、２つの経路を通過した波の干渉によって生じるのである。だから、片方経路の波長等の波の性質に致命的な影響を与えれば、もう片方に影響しなくても、干渉縞は生じない。

ここで考えるべきことは、検出器を置くことが検出器を置いた側の経路に与える影響の程度である。検出器を置いていない側の経路に影響を与えないことは、干渉縞が半分残る根拠にはならない。検出器を置いた側の経路に致命的影響を与えてしまえば、干渉縞が半分残ることはあり得ない。また、いずれの経路にも影響を与えないなら、干渉縞が半分消えることはあり得ない。

このような与太話は、量子力学を根本的に誤解している疑似科学特有のものである。干渉縞を作り出すのは、量子の波的性質であって粒子的性質ではない。その干渉縞が点描状になることが粒子的性質がもたらす結果であり、干渉縞の全体像は粒子的性質とは関係がない。以上のことを正しく理解していれば、片側検出器が意味を持たないことは容易に理解できるはずである。

運動量に「影響しない」監視装置

測定による擾乱の影響を受けないで通過スリットを検出する方法をScully,Walther,Englertが提唱している。しかし、その論文は明らかに波の通過スリットを検出している。

1989年にScully,Walther⁷⁾とEnglert⁸⁾の3人は,粒子と運動量のやり取りをしない装置でも,経路の識別ができるというモデルを提唱した.

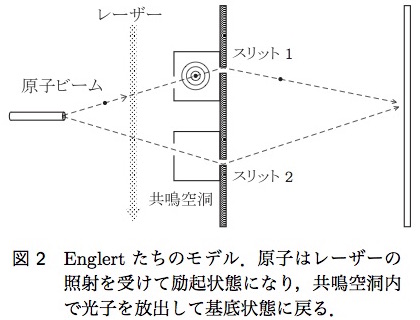
彼らの案では2つのスリットの直前に共鳴空洞(中空の金属箱)を置く(図2). 飛んでいる原子が空洞に入る前に,原子にレーザーを当てて励起状態にしてやる. 原子は2つの共鳴空洞のうち一方の内部で光子を放出して基底状態に戻る. したがって,空洞内の光子を調べれば原子がどちらのスリットを通ったかが分かる.
式で書くと,監視装置を備えていないときの原子の波動関数が
ψ(x)=ψ₁(x)+ψ₂(x)
であり,このうちψ₁(x)がスリット1を通過した波動関数,ψ₂(x)がスリット2を通過した波動関数である.スクリーン上の位置xに原子を見出す確率は
|ψ(x)|²=|ψ₁(x)|²+|ψ₂(x)|²+2Reψ₁^*(x)ψ₂(x)
で与えられる.ここでReψ₁∗ψ₂の項が干渉効果を表す.しかし,共鳴空洞を備え付けると,終状態は
ψ=ψ₁(x)⊗ξ1+ψ₂(x)⊗ξ2
となる. ここでξ₁は空洞1に光子が1個あるという状態であり，ξ₂は空洞2に光子が1個ある状態である. そうすると⟨ξ₁|ξ₂⟩=0であるから，原子が位置xに見つかる確率は
P(x)=|ψ₁(x)|²⟨ξ₁|ξ₁⟩+|ψ₂(x)|²⟨ξ₂|ξ₂⟩+2Reψ₁^∗(x)ψ₂(x)⟨ξ₁|ξ₂⟩=|ψ₁(x)|²+|ψ₂(x)|²
となり，干渉項は消える. 式(7)のような，原子と他の装置の状態が絡まった状態はエンタングル状態と呼ばれる. 原子の経路は空洞内の光子と相関を持ち，経路の違いは，光子の異なる状態，すなわち直交状態に記録されるため，原子の干渉項が消されるというのがScullyたちの説明である.
干渉と識別の相補性(谷村省吾) - 名古屋大学多自由度システム情報論講座

確かに、これなら測定による擾乱の影響は無視できる程度に小さいだろう。しかし、この思考実験では、量子もつれにより次の関係性が成り立つ仮定に基づいて式が立てられている。

「空洞1に光子が1個あるという状態」で波はスリット1のみを通過する
「空洞2に光子が1個あるという状態」で波はスリット2のみを通過する

この仮定が正しいかどうかは、ここでは問題としない。しかし、この仮定を置けば、実質的に単一スリット実験になるのだから、干渉項が失われるのは当然であろう。つまり、単一スリット実験では干渉縞が生じないという当たり前の結論を導いただけである。

いずれにせよ、波動関数から計算した確率の式から干渉項が消えるとしている。だから、これは波動性が失われないことを前提に計算されている。実質的に波の経路数が限定されるために干渉縞が生じなくなっているだけであって、波動性が失われているわけではない。

まとめると、この方法は、測定の擾乱以外の要素でも、干渉縞が生じない様に波の性質を変える場合があることを示しているだけである。波の性質に致命的な影響を与えずに粒子の通過スリットを特定しているわけではない。

尚、この思考実験を現実に行うことは極めて困難と考えられる。何故ならば、共鳴空洞(中空の金属箱)の横幅はμmサイズでなければならないからである。図を見れば分かる通り、粒子が共鳴空洞の中心を通過すると仮定すると、金属箱の横幅はスリット間隔より小さくする必要がある。二重スリット実験におけるスリット間隔は1μm以下〜50μmくらいであるため、金属箱の横幅はこれより小さくなければならない。マクロの観測装置をそのサイズで作るのは至難の技であろう。

片側経路屈折方式

だが、こうした解釈をせずに、あくまで、単一の粒子がどちらかのスリットを通過したという考えに固執すると、どのような結果が導かれるだろうか？具体的には、スクリーンに到達したときの粒子の位置情報をもとに、この粒子がスリットの一方を通った確率を計算するとどうなるか－という問いである。図7-10では、光子をスリットに平行方向（図のy軸方向）上向きにずらすようにガラスを設置してある。この二重スリットを用いると、スクリーンに到達した光子のy軸方向の分布をもとに、スリットＡとＢのどちらを通過してきたか、推定確率を計算することが可能となる。

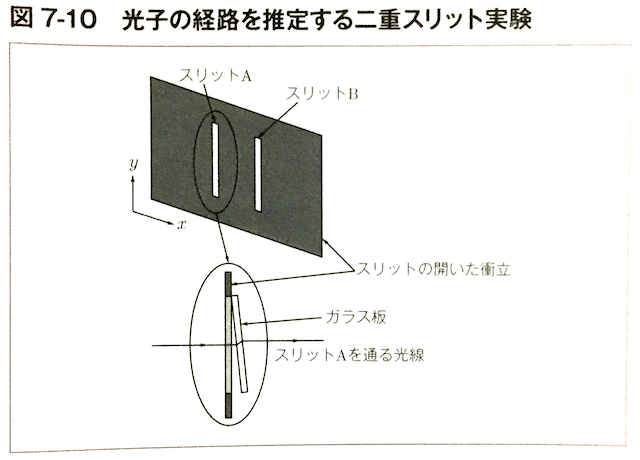
「量子論はなぜわかりにくいか」(ISBN-10:4774188182,ISBN-13:978-4774188188,著:吉田伸夫)P.181

二重スリット実験の結果と整合しないような理論に対しては、改めて検証するまでもなく二重スリット実験の結果によって否定されるから、こうした検証をする必要はない。こうした検証をする必要がある理論は、二重スリット実験の結果と整合する理論に限られる。そして、どのような理論であろうとも二重スリット実験の干渉縞と整合する理論である限り、この検証セットにおいて「スクリーンに到達した光子のy軸方向の分布」から「スリットＡとＢのどちらを通過してきたか、推定確率を計算する」ことは不可能である。

この検証セットにおいて「スクリーンに到達した光子のy軸方向の分布」から「スリットＡとＢのどちらを通過してきたか、推定確率を計算する」ことは、可観測量の１つである粒子の位置が片方のスリットのみを通過した何かによって決定される場合にのみ成り立つ。しかし、粒子の位置が片方のスリットのみを通過した何かによって決定されると仮定すると、二重スリット実験の干渉縞は説明できない。よって、二重スリット実験の干渉縞を説明するためには、例え、粒子が１つのスリットのみを通過すると仮定したとしても、粒子の位置は両方のスリットを通過する何かによって決定されなければならない。もちろん、両方のスリットを通過する何かとは波動性を示すもの＝波である。粒子の位置が一方のスリットのみを通過した何かによって決定されるとする理論は、二重スリット実験の結果によって否定されるから、こうした検証をする必要はない。

両方のスリットを通過する何かによって粒子の位置が決定されるなら、「ガラスを設置して」「上向きにずら」されたスリットＡの影響は、スリットＡを通った粒子も、スリットＢを通った粒子も、どちらも、ほぼ等しく受ける。よって、「スクリーンに到達した光子のy軸方向の分布」から「スリットＡとＢのどちらを通過してきたか、推定確率を計算する」ことは不可能である。例えば、二重解の理論とその派生理論では、「スクリーンに到達した光子の」x軸方向の分布から「スリットＡとＢのどちらを通過してきたか、推定確率を計算する」ことは可能である。しかし、どのような理論であろうとも、二重スリット実験と整合する理論である以上は、「スクリーンに到達した光子のy軸方向の分布」から「スリットＡとＢのどちらを通過してきたか、推定確率を計算する」ことは不可能である。

ところが、このようにして一方のスリットを通過した確率を計算すると、しばしば負の値が現れる（具体的な説明は、例えば、細谷暁夫著「『光子の裁判』再び」（日経サイエンス2014年01月号、p.34）などを参照されたい。ただし、この記事で示された解釈は、本書のものとは異なる）。このように、量子論では、古典論では当たり前のこととされる確率の正値性が、見かけ上で破れることがある。
「見かけ上で」と書いたが、確率が負になるのは、実際には起きていない過程に確率を割り当てようとしたからだと考えられる。
「量子論はなぜわかりにくいか」(ISBN-10:4774188182,ISBN-13:978-4774188188,著:吉田伸夫)P.181,182

この検証において「実際には起きていない過程に確率を割り当てようとした」こととは、明らかに、「スクリーンに到達した光子のy軸方向の分布」から「スリットＡとＢのどちらを通過してきたか、推定確率を計算する」根拠となる推定の内容である。すなわち、スリットＡを通過した粒子は高確率で上に到達し、スリットＢを通過した粒子は高確率で下に到達するという推定が、「実際には起きていない過程」なのである。このように「実際には起きていない過程に確率を割り当てようとした」のであれば、その結果として「確率が負になる」ということには何の驚きもない。

確率値で検証するならば、理論的に明らかに「実際には起きていない過程に確率を割り当てようとした」場合ではなく、理論に沿って「スクリーンに到達した光子の」x軸方向の分布から「スリットＡとＢのどちらを通過してきたか、推定確率を計算」した場合の確率値で検証すべきだろう。

後測定方式

ここまで説明した方式は、いずれも、スリットの直前、直後、または通過中に監視装置を置くやり方である。一方で、スリット通過からしばらく経過してから通過スリットを測定するやり方も提唱されている。後測定方式では、意図的に、スリット通過時に“which path marker”を付与する。そして、スリット通過からしばらく経過してから、その“which path marker”を利用して“which path information”を読み取ることで、通過スリットを特定できるという理屈である。尚、“which path marker”は“which path information”を測定するための準備であって、それ自体は“which path information”ではない。だから、“which path marker”を付与しただけでは、通過スリットを特定することはできない。

偏光操作方式

例えば、二重スリット量子消しゴム実験では、左右の波に逆回転の円偏光となる“which path marker”を付与する。この“which path marker”を付与すると、目視可能な干渉縞が生じなくなる。この場合、可逆的変化によって“which path marker”を付与しているため、“which path marker”のない元の状態に戻すことも可能である。当然ながら、“which path marker”のない元の状態に戻せば、目視可能な干渉縞が復活する。そして、一見すると、偏光の回転方法(スピン)を測定することで“which path information”が得られるかのように見える。しかし、この方法で“which path information”を得るには、可観測量は粒子の通過した側の波のみによって決定されなければならない。だが、二重スリット実験で干渉縞が観測される以上、可観測量は粒子の通過した側には関係なく両方のスリットを通過した波の複合的な影響によって決定されることは言うまでもない。よって、可観測量が粒子の通過した側の波のみによって決定されるのであれば、二重スリット実験では干渉縞が生じ得ないはずである。そして、“which path marker”をつけた時だけ粒子の通過した側の波のみによって可観測量が決定されると考える正当な理由もない。 “which path marker”を付与したことで干渉縞が消えることは、偏光等が干渉縞の必須条件を満たさないことによって容易に説明できるため、“which path marker”をつけた時だけ粒子の通過した側の波のみによって可観測量が決定されると考える正当な理由にはなり得ない。 “which path information”が得られていなかったとしても、全く同じ測定結果が得られることは明らかである。よって、次のように考えたほうが矛盾がない。

“which path information”は、実はランダムな測定結果(同じ強さの逆回転の円偏光の合成結果は常に直線偏光となるが、その場合のスピンの検出確率は半々となる)
“which path marker”付加時は、目視できる干渉縞(強度の変化)は生じていないが、目視できない干渉縞(偏光方向の変化)が生じている

干渉分離方式

遅延選択量子消しゴム実験では、“which path marker”を付与する段階で位相関係が致命的に乱されて、干渉縞が生じなくなる。この場合、“which path marker”からは、“which path information”を得ることも可能だが、乱された位相を補正する情報を得ることも可能である。ただし、その両方を得ることはできず、どちらか一方だけしか得られない。乱された位相を補正する情報を得るためには、“which path information”を諦めなければならない。この実験を簡単に説明すると次のようになる。

“which path marker”が位相を乱すため、干渉縞が見えなくなる
乱された位相を補正する情報を用いると、互いに相殺する逆方向の干渉パターンを抽出できる

このことは、通過スリットを特定する場合も波動性は維持されており、干渉縞が生じない場合にも目視できない干渉が生じていることを示唆している。この実験では、“which path information”と乱された位相を補正する情報のための情報は、どちらか一方しか得られないという相補性原理が成立している。しかし、この実験だけでは、相補性が必然的なのか偶然なのかまではわからない。よって、通過スリットの特定と干渉縞の関係性にも言及できない。

後測定方式まとめ

いずれの方法にしろ、“which path information”を測定してしまうと、目視可能な干渉縞を得ることはできない。 “which path information”を測定しない場合にだけ、目視可能な干渉縞を得ることが可能となる。 ネット上では「測定した経路情報を後から消すと干渉縞が復活する」と説明されることがあるが、これは明らかな間違いである。

その他

1993年にEichmannたちは興味深い実験結果を報告した. 彼らは2つの水銀イオンを空中に浮かべて静止させ，これらに偏光レーザー光を照射して，散乱光を観測した. つまり，2つの水銀イオンをダブルスリットに見立てた光干渉実験を行った. 光子は水銀イオンに当たったときに，イオンに角運動量を渡して，偏光状態が変化することがある.あるいは，角運動量のやりとりは起こらず，散乱光の偏光状態は入射光の偏光状態のままということもあり得る. そうすると，偏りが変化した光子は，どちらのイオンに当たったかという痕跡をイオンに残しており，干渉を起こさないだろうと考えられる. 一方で，偏りの変化のない光子は，どちらのイオンに当たったかという痕跡を残しておらず，したがって監視なしのダブルスリットと同じ状況になり，干渉を起こすと考えられる. 彼らはこういう実験をやって，予想どおりの結果を得た. つまり，カメラの直前に偏光フィルターを置いて，入射光と比べて同じ偏光状態を持つ光と，異なる偏光状態を持つ光とを選り分けて観測した.偏光変化のなかった光は干渉縞を示し，偏光変化を起こした光は干渉縞を示さなかった. この実験の場合，明らかに光子はイオンにぶつかって運動量のやりとりを行い，進路を変更している. それでも偏光状態さえ変わらなければ，きれいな干渉縞を作ったのである. したがって干渉縞が損なわれる理由を，運動量の誤差や位置のゆらぎのせいにすることには無理がある.
干渉と識別の相補性(谷村省吾) - 名古屋大学多自由度システム情報論講座

ここでは、ファインマンの思考実験や反跳運動量の測定等において干渉縞が生じない直接的理由が「運動量の誤差や位置のゆらぎ」であることを否定しているわけではない。この2つの水銀イオンを用いた実験では、粒子の経路を特定すると、「運動量の誤差や位置のゆらぎ」ではなく、偏光の不揃いにより干渉縞が消える。干渉縞が消える直接的理由が「運動量の誤差や位置のゆらぎ」ではない事例があるのならば、「不確定性関係が必ずしも干渉・識別の相補性の理由ではない」ことを示していると言えよう。

1998年にはDürr,Nonn,Rempeがルビジウム原子ビームの干渉実験を行った. 原子の超微細構造状態(原子核のスピンと電子の軌道運動の相互作用による微細なエネルギー差)の違いで原子の経路を識別すると干渉縞が消失することを彼らは示した. 彼らが用いた原子のビームは太くて，2方向に散乱されたビームは散乱領域では重なりっぱなしである. つまり原子ビームが，細く絞られた2本のビームに分離されてはいない. また彼らの実験では経路を識別するために，運動量の差ではなく，原子の内部状態の違いを用いている. したがって，位置と運動量の不確定性関係を当てはめるべき状況ではない. それにも関わらず，経路識別を行ったときには干渉縞は消え，識別をやめれば干渉縞は現れた. また，相補性不等式(8)も実験的に確かめられた. こうしてEnglertグループ対Storeyグループの論争は，Englertたちの勝利で決着がついた(と言ってよいと思われる). つまり，相補性は必ずしも不確定性関係の結果ではなく，相補性の方がより普遍的な概念である，という言い分の方が妥当である.
干渉と識別の相補性(谷村省吾) - 名古屋大学多自由度システム情報論講座

「超微細構造状態の違いで原子の経路を識別する」と、どのような過程で「干渉縞が消失する」のか定かではない。「原子核のスピンと電子の軌道運動の相互作用による微細なエネルギー差」＝「原子の内部状態の違い」を調べることが波のどの性質に影響を与えるのか不明である。いずれにしても、干渉縞が生じる条件の１つが崩れることによって干渉縞が消えるものと考えられる。

誤った説明の例

トンデモ解説等は以下に移動した。

Dr.Quantumによる二重スリット実験トンデモ解説
ネット上の二重スリット実験トンデモ解説
- 論理破綻例(「哲学的な何か、あと科学とか」 )
- 何と言うかアレ(南●さん)
- 「二重スリット実験を批判」？
- 「波長がずれるだけで二本線にはならない」？

このページの参照元
科学疑似科学を批判する疑似科学意識解釈コペンハーゲン解釈コペンハーゲン解釈トンデモ解説遅延選択量子消しゴム実験トンデモ解説二重スリット実験(疑似科学からの脱洗脳) Dr.Quantumによる二重スリット実験トンデモ解説ネット上の二重スリット実験トンデモ解説二重スリット量子消しゴム実験二重スリット量子消しゴム実験(旧) 二重スリット量子消しゴム実験トンデモ解説二重スリット量子消しゴム検証実験の提唱隠れた変数理論 Hotta解釈多世界解釈多世界解釈トンデモ解説光子の裁判射影仮説デコヒーレンス量子力学量子ポテンシャル理論シュレーディンガーの猫確率力学波動関数波動関数トンデモ解説波動性と粒子性の二重性波動性と粒子性の二重性トンデモ解説