相対性理論
よくある誤解
さて、一般の人は、相対性理論についてどのように理解しているだろうか。 おそらく、多くの人の理解は次のようなものではないか。
天才アインシュタインが、当時、誰も思いつかなかった高度な理論を唐突に発表した。
当時は、誰もが彼の理論を疑ったが、その後、彼が正しいことが証明された。
このような誤解が多いせいか、相対性理論は疑似科学による詐欺行為に悪用されやすい。
しかし、実際の相対性理論は一人の天才によって生み出されたものでも、唐突に発表されたものでもない。 過去の理論の蓄積を元に、それらを順当な思考で辻褄の合うように解釈したら、あら不思議、こんな理論が出来ました。 ・・・が相対性理論の真実である。
歴史的経緯
以下に、相対性理論が生まれる歴史的経緯を説明する
折り合いの悪い物理法則
当時の物理学者は次の物理法則の折り合いの悪さに頭を悩ませていた。 何れも法則も実験結果と良く一致し、正しい法則であると信じられていたのに、これらの間には致命的矛盾が生じていた。 ただし、ガリレイ変換とニュートン力学の間には何の矛盾もない。これらに矛盾するのは、マクスウェルの方程式である。
ガリレイ変換
異なる非加速度運動系の物体の物理的性質は、ガリレイ変換(相対速度を使った直線的変換)を行うだけで同じ式で表すことが出来る。
ニュートン力学
ニュートンが発見した力学法則で次の三つの法則から成り立つ。
- 第一法則=慣性の法則
- 第二法則=運動方程式
- 第三法則=作用反作用の法則
これらの法則は、ガリレイ変換が成り立っている。 これを別の言い方をすると、ガリレイ不変(ガリレイ変換に対して不変)とも言う。
マクスウェルの方程式
マクスウェルの方程式は、それまでの電気理論と磁気理論を一つに統合した電磁理論の性質を示す連立微積分方程式である。 しかし、マクスウェルの方程式はガリレイ変換と折り合いが悪かった。
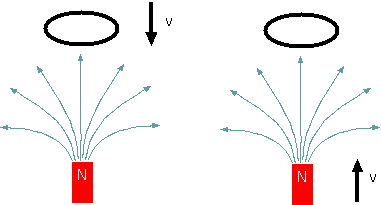
もう一つ、アインシュタインが疑問としたのはおなじみの電磁誘導をどのように解釈するかである。 アインシュタインの考察した現象とは少し違うが、以下のような現象を考えよう。 磁石にコイルを近づける(左図)、あるいはコイルに磁石を近づける(右図)、このどちらを行ってもコイルには電流が流れる。 この二つの現象は、「相対的に」考えるならば、全く同じものである。 というのは、左図の状態を、コイルと同じ速さで同じ方向に動いている人がみれば、まさに右図の状態が見えるはずだからである。 しかし電流の発生する原因の解釈は同じではない。
右図の場合、コイルに電流が流れる理由は、「磁束密度の変化によって渦を巻くような誘導電場が発生したから」(rot→E=-[(∂→B)/(∂t)])である。 一方、左図の場合、電流が流れる理由は「磁場中を電子が下向きに動いたので、ローレンツ力によって電子が動かされたから」である。
くわしい計算は後でもう一度実行するが、どちらの立場で計算しても流れる電流は同じになる。 このように、同じ現象のように見えるのに、違う物理法則によって起っているかのごとく、説明が2種類ある。 これはアインシュタインにとっては受け入れがたいことであった。 アインシュタインによる特殊相対性理論の最初の論文のタイトルは「運動する物体の電気力学について」(ZurElektrodynaikbewegterKörper)という、どちらかというと地味なものであるが、それはこのような電磁気に関する疑問から話が始まっているからである。
以上のように、相対論の目指すことは、「どんな立場で見ても物理法則は同じである」ということである。 動いている場合と止まっている場合は区別できず、「動いている時のための物理法則」を別に用意する必要はない。 前節でみたように、力学の法則はそうなっているが、電磁気の法則はそうなっていない(ように見える)。
もっと分かりやすい事例を挙げる。 マクスウェルの方程式を解くと、光速は、透磁率と誘電率(何れも物質固有の値)から導かれる定数となる。 では、何に対して定数なのか、光速が定数となる座標系を特定する必要がある。
エーテル仮説
当時の物理学者は、絶対静止系を考えた。 そして、光速は絶対静止系に対して定数となるのであって、相対速度が定数になるわけではないとして、物理法則の辻褄合わせを行った。 そして、当時有力だった光の波動説と併せて、宇宙はエーテルという未発見の媒質で満たされていて、光はエーテルを伝わる波であり、エーテルが絶対静止系を作っていると考えた。
アルバート・マイケルソンとエドワード・モーリーは、絶対静止系と地球の速度差「エーテルの風」を検出しようとして光速度の等方性干渉実験を行った。 当時、地球が太陽の周りを公転していることが知られており、その公転速度も分かっていた。 そこで、地球の公転方向(東西)と公転の影響のない方向(南北)の光の伝達時間の差を計れば「エーテルの風」を検出できると考えられた。 大凡の光の速度から、必要な精度も計算され、その精度を満足する実験方法が使われた。 もし、仮に、ある瞬間、速度差が0となっても、地球は公転しているのだから、別の季節で試せば「エーテルの風」が観測されるはずであった。 ところが、現実に観測された速度差は常に測定限界以下であった。 実験時刻や季節を変えて何度実験をしても結果は変わらなかった。 つまり、絶対静止系と矛盾する結果が出たのである。
特殊相対性理論
当時の物理学者は、マイケルソン=モーレーの実験結果に驚いた。 そして、エーテル仮説を維持しようと辻褄合わせを行った。 その辻褄合わせに、ローレンツ、フィッツジラルド、ポアンカレ等が挑戦した。
そんなある日、アインシュタインは、エーテル仮説に頼らないもっと自然な辻褄合わせを発表した。 それが特殊相対性理論である。 そこに用いられたローレンツ変換式は、ローレンツが発表した式と全く同じ(数学的には同じ辻褄合わせをしているのだから同じ式になるのは当然)であるが、エーテル仮説を維持するかどうかの基本的な考え方に違いがあった。
実は、特殊相対性理論の主要部分であるローレンツ変換、加速による質量の増加(定性的には加速によって古典的質量が増加すると見なせなくもないが、その質量を普遍的値として再定義することはできない)、光速度不変、光速度=加速限界等は、既に、ローレンツやポアンカレによって発表済みであった。 それ故に、特殊相対性理論におけるアインシュタイン独自の功績は少ないと言われる。
一般相対性理論
当時の物理学者は特殊相対性理論以上のものを求めなかったが、アインシュタインは満足しなかった。 なぜなら、特殊相対性理論では定式化可能な範囲に限界があったからである。 例えば、双子のパラドックスを考える。 同じような運動をしているように見える場合として、双方が重力の影響を受けずにロケットが加速度運動をしている場合と、双方が重力の影響を受けてロケットが静止している(地球が加速度運動をしている)場合があるが、現実問題として両者の区別はつかない。 何故なら、重力に対して自由落下している系からは、その受けた重力を計測することはできないからである。 特殊相対性理論では、前者を定式化できるが、後者は定式化できない。 よって、この事例について、特殊相対性理論では、双方が外部から重力を受けていないという仮定においてのみ定式化可能であり、両者が区別できないという現実に即した定式化はできない。
アインシュタインは、あらゆる運動を定式化しようとして、電気力と重力(万有引力および慣性力)の統合理論である一般相対性理論を完成した。 ちなみに、アインシュタインを天才と呼ぶには、少々、数学力に欠けていた。 友人グロスマンから数学的手法としてリーマン幾何学を学び、四苦八苦して、アインシュタイン方程式としての定式化に成功したと言う。 一般相対性理論の功績の半分はグロスマンにあるとも噂される。
水星の近日点の移動、太陽近傍での恒星の光の屈曲率が一致する等の数々の証拠により、一般相対性理論はほぼ正しいと認められているが、若干の修正の余地があるのではないかとも考えられている。
相対性理論関係年表
ネットのあちらこちらから拾ってきたのでかなり怪しい年表であるが、歴史的経緯を知るには十分であろう。
| 年 | 月 | 日 | 人物 | 研究内容 |
|---|---|---|---|---|
| 1609 | ケプラー | ケプラーの第一第二法則を発表 | ||
| 1619 | ケプラー | ケプラーの第三法則を発表 | ||
| 1632 | ガリレオ | 等速運動系における相対性原理(ガリレイ変換)を発表 | ||
| 1664頃 | ニュートン | 力学の3法則を見出す | ||
| 1865 | マクスウェル | マクスウェルの方程式を発表し電磁波の存在を預言 | ||
| 1887 | マイケルソンとモーレー | 光速度の等方性干渉実験でエーテル観測されず | ||
| 1888 | ヘルツ | 電磁波の実証実験 | ||
| 1891 | エートヴェーシュ | 重力質量と慣性質量の同一性の実験 | ||
| 1892 | ローレンツ | ローレンツ短縮仮説の論文を発表 | ||
| 1892 | フィッツジェラルド | ローレンツ-フィッツジェラルド短縮を発表 | ||
| 1895 | ローレンツ | ローレンツ短縮仮説の追加論文を発表 | ||
| 1896 | マルコーニ | 無線電信の実用化 | ||
| 1899 | ポアンカレ | ポアンカレの相対性原理を発表 | ||
| 1901 | カウフマン | 高速電子の比電荷(質量)の増加を粗測定(相対性理論とは一致しない) | ||
| 1902 | アブラハム | … | ||
| 1904 | ローレンツ | ローレンツ短縮仮説をローレンツ変換にまとめる | ||
| 1905 | 6 | 30 | アインシュタイン | 特殊相対性理論の論文を発表 |
| 1905 | 9 | 27 | アインシュタイン | 特殊相対性理論の追加論文(E=mc^2)を発表 |
| 1907 | 12 | アインシュタイン | 一般相対性理論の前段階論文(重力による光の屈曲)を発表 | |
| 1909 | ブーヘラー | 高速電子の比電荷(質量)の測定結果が相対性理論と一致 | ||
| 1911 | アインシュタイン | 一般相対性理論の前段階論文を発表 | ||
| 1912 | アルゼンチン隊 | 皆既日食の観測を計画するが雨で流れる | ||
| 1914 | アインシュタイン | 一般相対性理論の前段階論文を発表 | ||
| 1915 | アインシュタイン | 一般相対性理論の前段階論文(水星の近日点の移動)を発表 | ||
| 1915 | 11 | 20 | ヒルベルト | アインシュタインの論文を元に重力場の方程式を発表 |
| 1916 | アインシュタイン | 一般相対性理論の完成論文を発表 | ||
| 1916 | アインシュタイン | 一般相対性理論の追加論文(重力波)を発表 | ||
| 1917 | アインシュタイン | 一般相対性理論の追加論文(宇宙項)を発表 | ||
| 1918 | アインシュタイン | 一般相対性理論の追加論文を発表 | ||
| 1918 | アインシュタイン | 一般相対性理論の追加論文(重力波)を発表 | ||
| 1919 | 5 | 29 | イギリス観測隊 | 皆既日食時に太陽近傍の恒星の光の屈曲を観測 |
| 1919 | 11 | 6 | イギリス観測隊 | 観測結果が一般相対性理論と一致したと発表 |
トンデモ事例
トンデモ事例の解説は相対性理論トンデモ解説に移動した。
- このページの参照元
科学 当サイトの科学項目の目的 ベルの不等式 納得論法 コペンハーゲン解釈トンデモ解説 決定論と自由意志 ネット上の二重スリット実験トンデモ解説 地震爆発論(笑) 石田昭氏の主流学説に対する無理解 「○○学界は閉鎖的」論法 地球温暖化懐疑論者たち 槌田敦氏が似非科学者の証拠 隠れた変数理論 Hotta解釈 量子力学 相対性理論トンデモ解説
このページへのご意見は節操のないBBSにどうぞ。
総合案内
科学一般
疑似科学等
- 疑似科学
- 数学や科学への無理解
- 疑似科学を批判する疑似科学
- STAP細胞論文捏造事件
- CCS地震原因説
- 地球温暖化懐疑論
- 疑似科学者列伝