ベルの不等式

• 局所性
• アインシュタインが指摘した量子もつれの相関性
  • 非局所的相関
  • 局所的かつ充足理由の法則を満足する場合
  • 充足理由の法則を満たさない理論
• ベルの不等式(ベルの限界)
  • 問題整理
  • 検証は十分か?

局所性 

非局所的な理論では、力は、時間経過なしに遠隔地に伝搬する。 一方で、局所的な理論では、ある地点の現象は、まず、その地点の周囲に影響を与え、さらに、その周囲に影響を与え、ということを繰り返して、最終的に遠隔地に影響を及ぼす。 結果、局所的な理論では、力は、光速を超えない有限の速度で遠隔地に伝搬する。

ニュートン力学における万有引力は非局所的な遠隔相互作用として扱われていた。 一方、マクスウェルの方程式は電磁気の局所的理論であり、一般相対性理論は重力の局所的理論である。 それ以降、物理学で扱うあらゆる力は局所的な力であると解釈されている。

以上のような経緯から、今日では、物理法則の局所性を否定することは、確立した理論をひっくり返す大ごととなる。 一方で、ブラックボックスの外からのaccessibleとならない非局所性は相対性理論に反しないとする指摘もある。 例えば、井元信之氏は、以前は、「相対論を満たさない」という理由で量子ポテンシャル理論を認めていなかった。

しかし、ボームの解釈は、あまりに信じることができないというのが正直なところです。 相対論を満たさないという点が受け入れられない。

「SF小説がリアルになる　量子の新時代」(ISBN-10:4022732873,ISBN−13:978-4022732873,著:佐藤文隆/井元信之/尾関章)kindle版p.173-174

尚、その後、井元信之氏は次のように態度を改めている。

その後、私は「Bohmの理論」すなわち「非局所隠れた変数の理論」を「問答無用」とまで拒絶することはなくなった。

決定論的量子力学? ボーム理論はどこまで行くか?(大阪大学基礎工学研究科 井元信之) - 高知工科大学

その理由について次のように説明されている。

この意味で、ブラックボックスの中では実在としての変数RやSが非局所的に動き回るモデルである。

もちろんブラックボックスの外にいる我々は、その応答を利用して超光速通信をすることはできない。

「非局所性」の意味：

Bohmの量子ポテンシャルの非局所性とは、「ブラックボックスの中で超高速で伝わる」ことを意味。

「影響が空間を連続的に伝わる」意の局所性は、ブラックボックスの外からのaccessibleなものの性質。

決定論的量子力学? ボーム理論はどこまで行くか?(大阪大学基礎工学研究科 井元信之) - 高知工科大学

常識で考えて、真っ当な科学者であれば「相対論を満たさないという点」を受け入れるようになった、すなわち、相対性理論を否定するようになったとは考えにくい。 よって、これは、局所性の制限はブラックボックスの外からのaccessible(アクセス可能)な現象のみに適用されるのであって、ブラックボックスの外からのaccessible(アクセス可能)でない所で非局所性が現れても相対性理論には反しないという意味である。 これは、事象の水平面内のような現実的に問題にならない所で物理法則が破綻する特異点があっても問題ないのと同じであろう。

アインシュタインが指摘した量子もつれの相関性 

EPR論文では、２つの粒子１と２の相対位置(位置座標の差)および全運動量(運動量の和)が同時に確定できることが波動関数を使って示され、その上で、相対的位置と全運動量がわかっている２つの粒子が十分に離れたときに、一方の粒子に対して観測を行うケースが検討された。 粒子１の位置を測定すると、相対位置の値から粒子２の位置が直ちに判明する。 同じように、粒子１の運動量を測定すると、粒子２の運動量がわかる。

---

粒子２から十分に離れた時点で粒子１の観測を行う場合、測定するのが位置であっても運動量であっても、粒子２の状態は（充分に離れているので）擾乱されず、それ以前の状態からは変化してないはずである。 とすると、粒子２は、粒子１の観測が行われる以前から位置と運動量が確定した状態にあり、位置と運動量は同時に確定できないとする量子論の基礎に抵触するのではないか？ －これが、EPR論文で提起された問いである(科学史的に正確なことを言うと、これはアインシュタインが提起した問いで、３人で議論した内容をまとめる形でポドルスキーが単独執筆したEPR論文では、論点が少しずれている)

粒子１で位置と運動量のどちらかを観測するかに応じて、粒子２の状態が瞬時に変化すると仮定すれば、粒子１の観測後に粒子２で確定しているのは位置か運動量のどちらかだけなので、量子論の基礎とは矛盾しない。 しかし、２つの粒子が十分に離れているにもかかわらず、粒子１の観測で粒子２の状態が変化するのは、一種の遠隔相互作用が起きたことになり、光速を越える相互作用を禁じた相対論の原理に矛盾する。 この遠隔相互作用が、アインシュタインが「spooky」と呼んだものである。

「量子論はなぜわかりにくいか」(ISBN−10:4774188182,ISBN−13:978-4774188188,著:吉田伸夫)P.159,160

「波動関数を使って示され」と言われても一般人向けではないので、もう少しわかりやすく噛み砕いて説明する。

特定の原子から同じ方向に直線偏光した２つの光子が放出されることがある。 この現象を利用して、偏光の相関を調べる実験を考えよう。

「量子論はなぜわかりにくいか」(ISBN−10:4774188182,ISBN−13:978-4774188188,著:吉田伸夫))P.167

ベルの不等式の検証はスピンを用いることが多いが、一般向けには難易度を下げるために偏光で説明されることが多い。 尚、この本の説明では何が言いたいのか、素人が読んでもさっぱり意味がわからないと思われるので、もう少しわかりやすく説明しょう。

そこで、２つの偏光板（光子１と光子２を照射する偏光板１と偏光板２）の軸を角度θだけずらしたセットアップで何度も実験を繰り返し、Ｒの統計的な平均値を求めることを考えよう。

「量子論はなぜわかりにくいか」(ISBN−10:4774188182,ISBN−13:978-4774188188,著:吉田伸夫)P.169

ようするに、光子１の照射方向に偏光板１を置き、光子２の照射方向に偏光板２を置くということである。

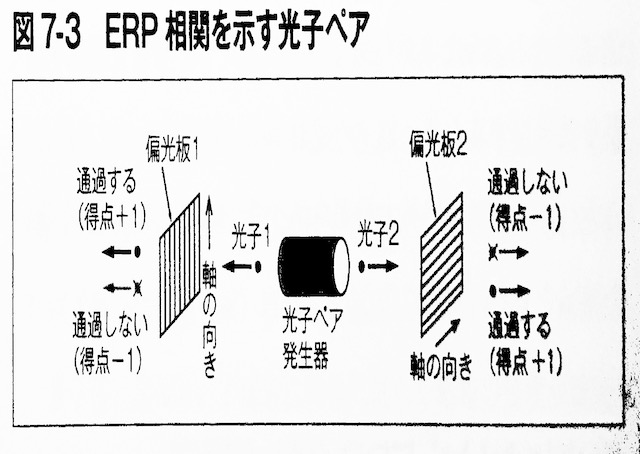
「量子論はなぜわかりにくいか」(ISBN−10:4774188182,ISBN−13:978-4774188188,著:吉田伸夫)P.168

偏光板の性質は偏波・偏光を読んでもらいたい。 尚、ここで言うＲは次のとおりである。

相関を数値で表すために、光子が偏光板を通過したときには＋１、通過しなかったときには−１という得点を与え、２つの光子の得点の積Ｒを見ることにする。

「量子論はなぜわかりにくいか」(ISBN−10:4774188182,ISBN−13:978-4774188188,著:吉田伸夫)P.169

この結果を光学的な波動性と確率規則だけで計算してみよう。

偏光の向きと偏光板の性質は偏波・偏光で説明する。 偏光の向きと偏光板の向きの角度差がφの場合、通過できる確率Pと通過できない確率Qはエネルギーベース透過率に依存するため次のとおりとなる。

• P=cos²⁡φ
• Q=sin²⁡⁡φ
• P-Q=cos⁡2φ

ここで、ペア間の偏光の向きが同一であると仮定する。 偏光板の向きの角度差がθの場合で、かつ、ペアの一方における偏光の向きと偏光板の向きの角度差がφの場合の確率は次のとおりとなる。

• P_a=cos²⁡φ
• Q_a=sin²⁡⁡φ
• P_a-Q_a=cos⁡2φ
• P_b=cos²⁡(φ+θ)
• Q_b=sin²⁡⁡⁡(φ+θ)
• P_b-Q_b=cos⁡2⁡(φ+θ)

この時の得点の積R(a,b)は次のとおりとなる。

R⁡(a,b)=P_a∙P_b+Q_a∙Q_b-(P_a∙Q_b+Q_a∙P_b )=(P_a-Q_a )∙(P_b-Q_b )=cos⁡2φ∙cos⁡2(φ+θ)={cos⁡2θ+cos⁡(4φ+2θ)}÷2

φを０°から360°まで平均化した〈R⁡(a,b)〉は積分で計算できる。 cos⁡2θの項は定数であるから、平均化しても変わらない。 cos(4φ+2θ)の項はcosをちょうど４周分平均化するので０となる。 結果、〈R⁡(a,b) 〉=(cos⁡2θ)／２となる

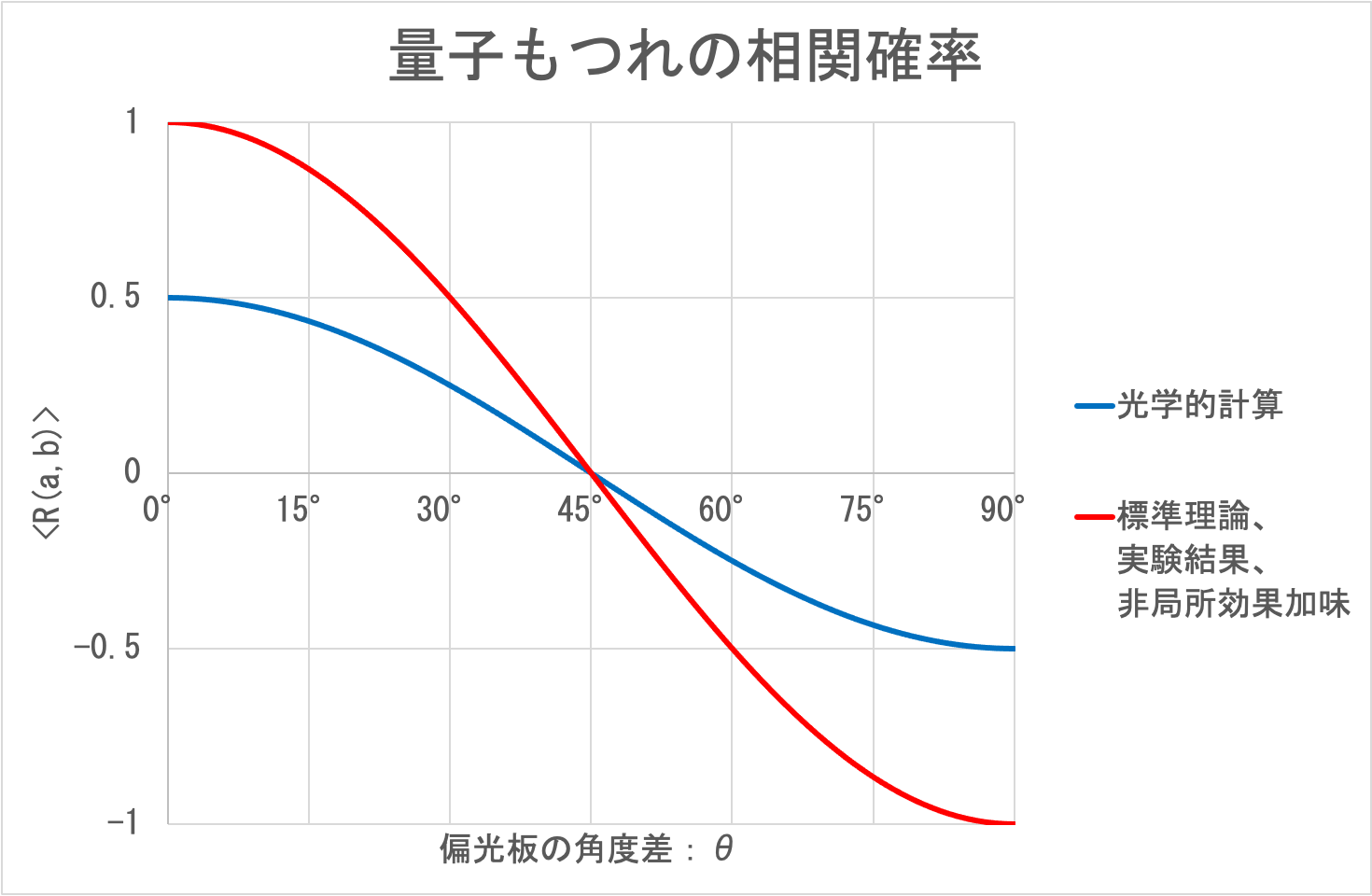
しかし、実験結果は計算の倍の値となっている。 ペア間の偏光の向きが同一ではなく、その差が定数値となる場合は、このグラフを横方向にシフトした値となる。 その場合も、実験結果とは一致しない。 また、ペア間の偏光に全く相関性がなければ〈R⁡(a,b) 〉=０となるから、これも実験結果とは一致しない。 よって、光学的な波動性と確率規則だけで説明するためには、ペア間の偏光の向きが定数値ではない特殊な相関性となる必要となる。

非局所的相関 

例えば、先に偏光板に到達した方が偏光板を通過した場合に他方の偏光の向きを通過した偏光板と同じ向きに変え、かつ、先に偏光板に到達した方が偏光板を通過しなかった場合に他方の偏光の向きを通過した偏光板と垂直な向きに変えると仮定すると、この実験結果と辻褄が合う。 a側が先に偏光板に到達し、かつ、a側が偏光板を通過した場合に、b側の偏光がa側の偏光板と同じ向きに変えられてしまうと仮定すると、a側が偏光板を通過した場合のb側の確率は次のとおりとなる。

• P_bp=cos²⁡⁡⁡θ
• Q_bp=sin²⁡⁡θ

a側が先に偏光板に到達し、かつ、a側が偏光板を通過しなかった場合に、b側の偏光がa側の偏光板と垂直向きに変えられてしまうと仮定すると、a側が偏光板を通過しなかった場合のb側の確率は次のとおりとなる。

• P_bq=sin²⁡⁡⁡θ
• Q_bq=cos²⁡⁡⁡θ

よって、この時の得点の積R(a,b)は次のとおりとなる。

R⁡(a,b)=P_a∙P_bp+Q_a∙Q_bq-(P_a∙Q_bp+Q_a∙P_bq )=(P_a+Q_a )(cos²⁡⁡⁡⁡θ-sin²⁡⁡⁡⁡θ )=cos⁡2θ

同様に、b側が先に偏光板に到達した場合を計算しても、同じ計算結果となる。 R⁡(a,b)が常にcos⁡2θとなるならば、φを０°から360°まで平均化した<R⁡(a,b)>もcos⁡2θとなる。 これは実験結果と一致する。

ここで、２つの偏光板間の距離をＬ、２つのペアの偏光板への到達時間差をΔtと定義する。 Ｌを十分に長く、かつ、Δtを十分に短くし、Ｌ÷Δtが光速を遥かに超えるようにしても、実験結果は変わらない。 偏光板の向きに応じた何かが局所的に伝播する可能性も考慮して、偏光板を常時ランダムで動かしても、実験結果は変わらない。 だから、ペアの一方が他方に作用するような理論でこの実験結果を説明しようとすると、ペアの一方から他方への光速を遥かに超える情報伝達が必要となり、局所性が崩れる。 言い換えると、このような作用では、局所的な理論を構築できない。

局所的かつ充足理由の法則を満足する場合 

既に説明した通り、隠れた変数が偏光板の向きに依存すると局所性が崩れる。 言い換えると、局所性を満足するためには、隠れた変数が偏光板の向きに依存してはならない。 しかし、隠れた変数が偏光板の向きに依存しないという条件をつけると、実験結果の相関性を説明できる理論の構築は極めて困難となる。

実験結果では、θ＝0°のときに<R⁡(a,b)>＝１となっているが、これはペアの測定結果が全て一致することを意味する。 １≦R⁡(a,b)≦１であるから、<R⁡(a,b)>＝１となるためには、R(a,b)は常に１でなければならない。 偏光の向きがθに依存しないと仮定すれば、φ＝0°またはφ＝90°の場合は、ペアの偏光の向きが等しい限り、R(a,b)が１になる。 しかし、φ＝45°となる場合は、R(a,b)=０となってしまう。 というのも、光学的には通過確率は50%であり、偏光の向き以外に通過の有無を決める変数がない場合は、完全にランダムとなるからである。 ランダムな結果なら、ペアの通過の間に相関性がなくなるため、R(a,b)=０となる。 φ＝45°でもR⁡(a,b)＝１とするためには、偏光の向き以外に偏光板の通過の有無を決める隠れた変数が必要となる。 そして、それは光学的な通過確率と矛盾しないことが必要である。 では、あらゆるφ値およびθ値に対してこのような相関性が働く理論を構築することは可能だろうか。

ここで、全ての光子が隠れた変数値０＜Ｎ＜１を持ち、かつ、量子もつれのペアの光子が全く同じＮ値を持つと仮定しよう。 Ｎは、θ値やφ値に依存せず、かつ、光子が誕生したときに持つ変数値であれば、疑う余地のない完全な局所的隠れた変数理論である。 そして、Ｎ値の発生確率が全ての値で一様であり、かつ、Ｎ＜cos²φで偏光版を通過すると仮定すれば、光学的な通過確率cos²φとも全く矛盾しない。 そして、２つの偏光の向きが等しく、かつ、Ｎ値が等しい限り、φ値がいくらであろうともθ＝0°のときには100％相関するので、R(a,b)は常に１となる。 つまり、θ＝0°のときは、ペアの測定結果が全て一致するから<R⁡(a,b)>＝１となり、実験結果と一致する。 言い換えると、R(a,b)はＮ値にもφ値にも依存することなく常に１となるから<R⁡(a,b)>＝１となるのである。

では、θ＝90°のときはどうなるか。 ２つの偏光板の閾値cos²⁡⁡⁡φとcos²⁡⁡⁡(φ+θ)のいずれか小さい方をＴ_min、大きい方をＴ_maxとすると、任意のφおよびθにおいて、Ｎ＜Ｔ_minおよびＴ_max≦Ｎのときにペアの測定結果が一致する。 同様に、Ｔ_min≦Ｎ＜Ｔ_maxのときにペアの測定結果が不一致となる。 θ＝90°のときの閾値をグラフに描くと、相関の様子がよく分かる。

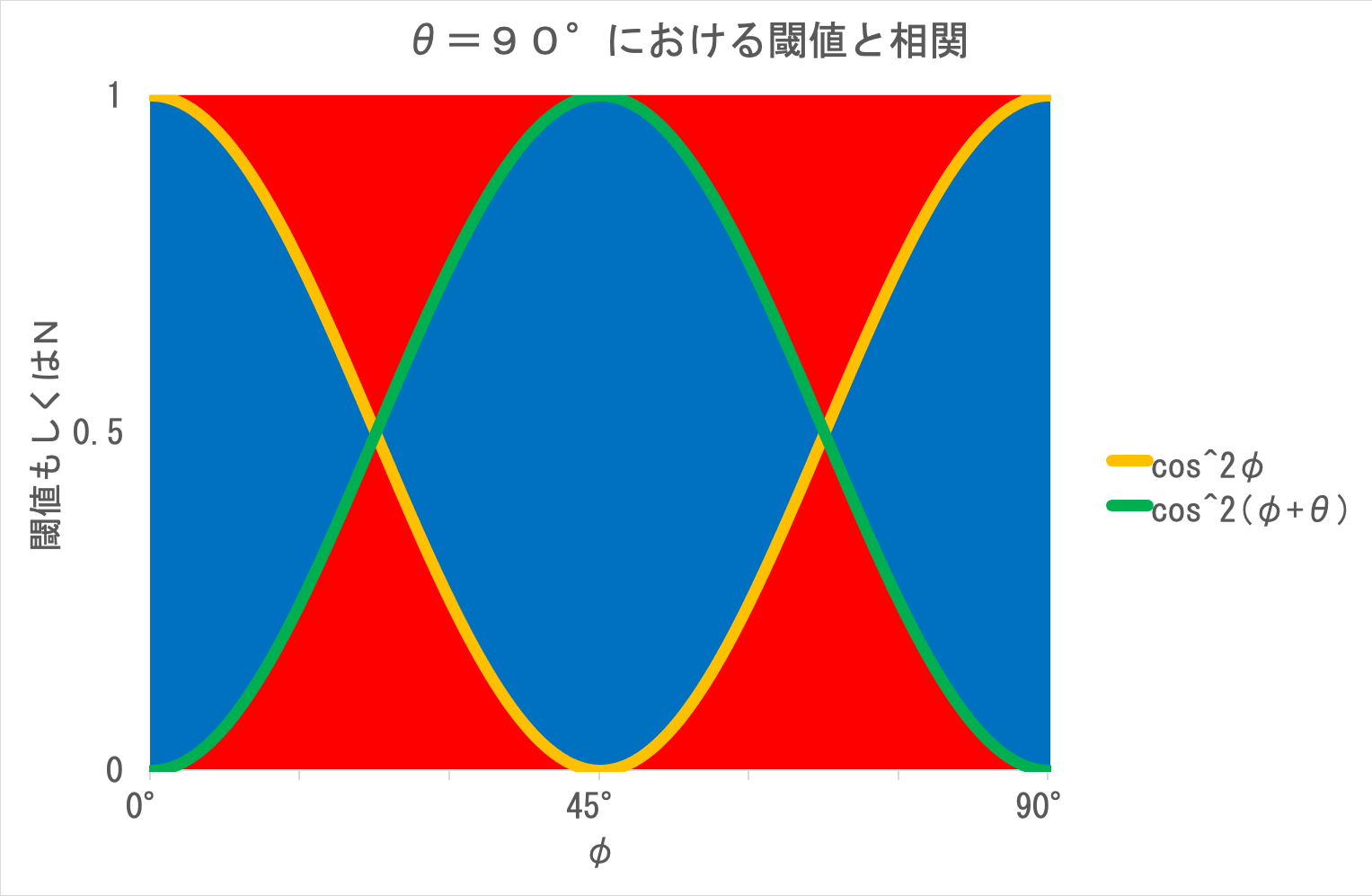
グラフの赤の領域はペアの通過結果が一致し(R⁡(a,b)＝１)、青の領域は一致しない(R⁡(a,b)＝−１)。 <R⁡(a,b)>はR⁡(a,b)の平均値であるから次の数式で求まる。

• <R⁡(a,b)>＝（赤の面積×１＋青の面積×−１）÷全面積

よって、赤の面積が０の場合にのみ<R⁡(a,b)>＝−１となる。 グラフを見れば明らかなとおり、一致する場合と一致しない場合のそれぞれが一定確率で存在するので、<R⁡(a,b)>＝−１にならないことがわかる。 これは実験結果と一致しない。

以上のように考えると、θ＝0°とθ＝90°に限定しても、実験結果と一致する理論を構築することの困難さが良くわかろう。 ここでは、そうした理論が構築できないそうもないことを示唆できても、構築できないことを証明することは困難である。 その証明こそが、ベルの不等式であり、それは後で説明する。

充足理由の法則を満たさない理論 

アインシュタインは、充足理由の法則(一般に因果律と呼ばれているもの)を否定すると、局所的な理論ではこのような作用の説明がつかないと指摘した。 そして、局所的ではない作用を「薄気味悪い長距離相関」と呼び、充足理由の法則を否定する標準理論を批判した。 そもそも、充足理由の法則を否定すれば、この実験のような量子もつれのペアの相関関係を説明することはできない。 両者の測定結果が完全に独立して無作為に決まっていると仮定すると、この実験結果のような相関確率は生じ得ない。 何らかの因果関係で相関確率に影響を与えるなら、それは正しく充足理由の法則である。

ベルの不等式(ベルの限界) 

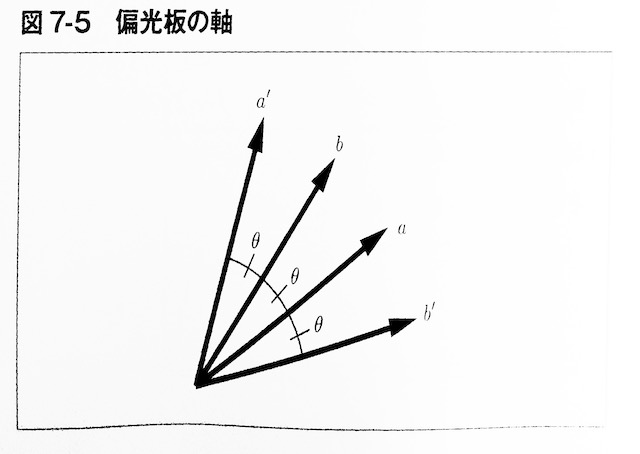
図7−5のように、偏光板１と２の軸が、それぞれaとa’、bとb’という２段階に切り替えられるものとする。

「量子論はなぜわかりにくいか」(ISBN−10:4774188182,ISBN−13:978-4774188188,著:吉田伸夫)P.169

充足理由の法則と局所性が両立する古典力学では常に次の不等式が成立するとされる。

−２≦〈R⁡(a,b)〉＋〈R⁡(a',b)〉＋〈R⁡(a,b')〉－〈R⁡(a',b')〉≦２

この限界値をベルの限界と呼ぶが、その証明は長くなるので省略する。

この実験結果も光学的な波動性と確率規則だけで計算してみよう。 図より、a,b間、a’,b間、a,b’間の角度差は全て等しく、a’,b’間の角度差はその３倍である。 そのことから、次の通り計算できる。

〈R⁡(a,b)〉＋〈R⁡(a',b)〉＋〈R⁡(a,b')〉－〈R⁡(a',b')〉＝(3cos⁡2θ-cos6θ)／２

この値はベルの限界を超えない。

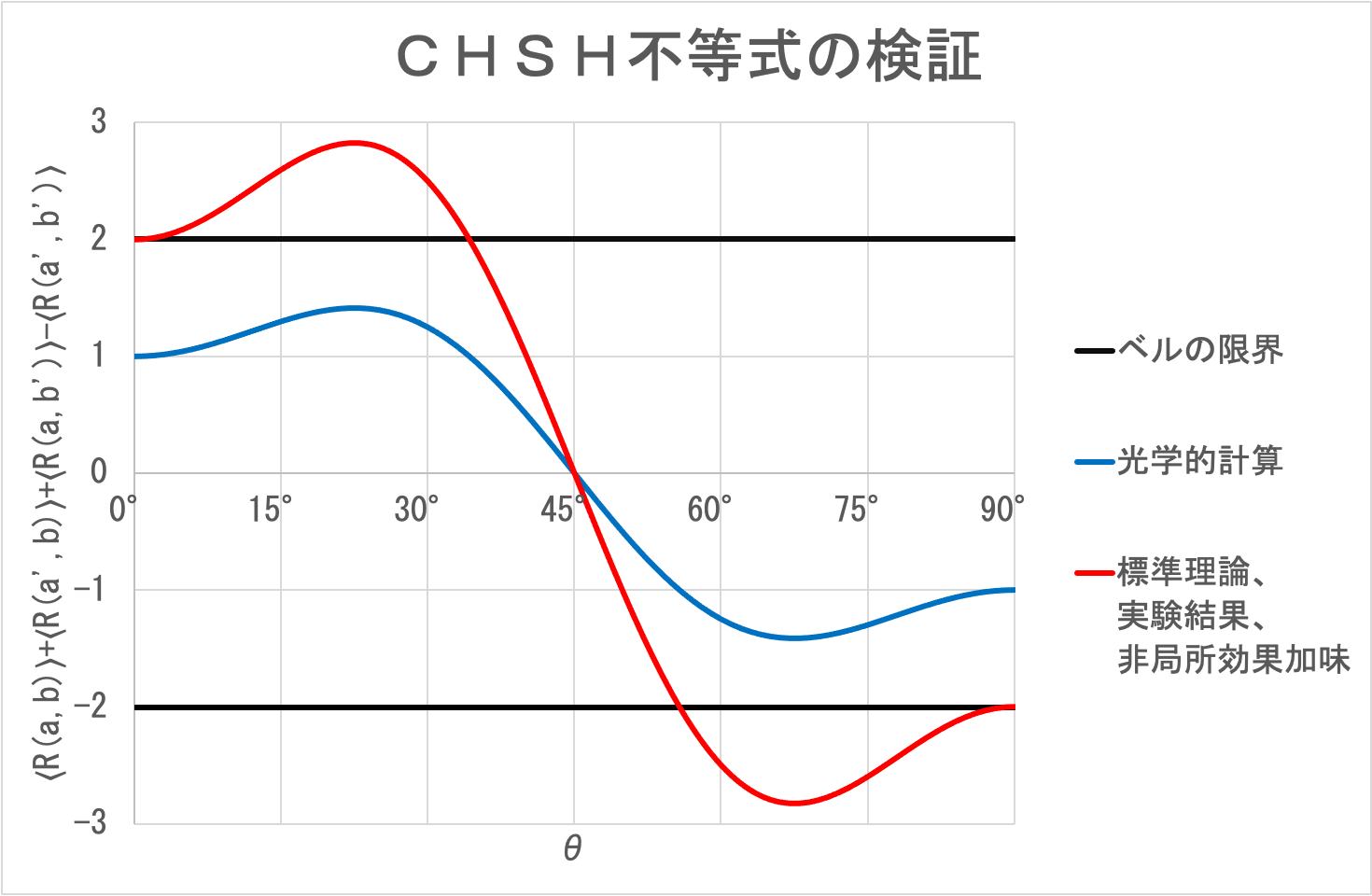
しかし、実際の実験結果はベルの限界を超えてしまう。 先ほど仮定したような、一方の通過結果が他方の偏光の向きを変えるような相関を仮定すると、この実験結果と一致する。

〈R⁡(a,b)〉＋〈R⁡(a',b)〉＋〈R⁡(a,b')〉－〈R⁡(a',b')〉＝3cos⁡2θ-cos6θ

いずれにせよ、結果はベルの限界を超えてしまう。 充足理由の法則が成立すると仮定すると、このような作用は局所的理論では説明できず、非局所的な長距離相関が必要になることを意味する。 つまり、隠れた変数理論は局所的ではないこととなる。 「薄気味悪い長距離相関」が否定理由となるなら、それは隠れた変数理論にもブーメランとして帰ってきてしまう。

問題整理 

ベルの不等式とその検証実験は次のことを示している。

• 充足理由の法則と局所性は両立しない
• 局所性を捨てれば、充足理由の法則を取り戻せる
• 充足理由の法則を捨てても、局所的な作用では説明できない

ベルの不等式の検証実験により、局所的隠れた変数理論が成立しないことがわかった。 しかし、充足理由の法則を捨てても局所的な作用では説明できないのだから、この問題は標準理論にも降りかかる問題である。 つまり、アインシュタインが指摘した「薄気味悪い長距離相関」の問題は何も解決していない。 非局所性を理由に隠れた変数理論を批判するなら、同じ批判は標準理論にもブーメランとして帰ってくる。

そして、先ほども説明した通り、充足理由の法則を否定すれば、この実験のような量子もつれのペアの相関関係を説明することはできない。 両者の測定結果が完全に独立して無作為に決まっていると仮定すると、この実験結果のような相関確率は生じ得ない。 何らかの因果関係で相関確率に影響を与えるなら、それは正しく充足理由の法則である。 それは局所性の有無とは全く関係がない。

百歩譲って、量子もつれのペアの相関確率を充足理由の法則なしで説明できると仮定しよう。 もしも、そうだとすれば、ベルの不等式は証明として何の役にも立たないことになる。 量子もつれのペアの相関確率が充足理由の法則の結果であると考えられるからこそ、その相関確率が局所性との両立と矛盾することを示すことで、充足理由の法則と局所性が両立しない作用の存在を認めざるを得なくなる。 しかし、量子もつれのペアの相関確率が充足理由の法則の結果ではないなら、たとえ、その相関確率が局所性との両立と矛盾するとしても、充足理由の法則と局所性が両立しない作用の存在は認められない。 何故なら、充足理由の法則の結果ではないなら、その結果は充足理由の法則とは無関係となるからである。

以上まとめると次のとおりとなる。

• 相関確率を充足理由の法則なしに説明できないなら、標準理論も次の両方を認めざるを得ない
  • 少なくとも、量子もつれの相関性は充足理由の法則に従った現象である
  • 少なくとも、量子もつれの相関性については非局所性がある
• 相関確率を充足理由の法則なしに説明できるなら、ベルの不等式の証明能力を否定することになる

つまり、ベルの不等式の検証実験では、隠れた変数理論より標準理論が優れていることを示せない。

検証は十分か? 

実は、検証実験は完全な証明ではないようだ。

ただし，抜け道を完全に防ぐのは難しい． たとえば，測定装置の設定の変更は完全にランダムに行われるわけではない，あるいは粒子源から放出されるすべての粒子対が測定されるわけではない，などの事実をよりどころに，「局所的な」理論を構成すること（例えば文献[１8]）は可能かもしれない． こういった可能性を完全に排除するのは困難である．

「量子という謎」(ISBN−１0:4326700750,ISBN−１3:978-4326700752,著:白井仁人・東克明・森田邦久・渡部鉄兵)P.45

ただ、こうした証明の不完全さを突いて局所的理論を構築したとしても、かなり歪な理論になるであろうから、その現実的な意味があるかどうかは疑わしい。 素直な理論を構築できると見込めるからこその隠れた変数理論なのであって、そこまでして歪な隠れた変数理論に拘る理由はあるまい。 以上の意味で、ベルの不等式の検証実験は、隠れた変数理論を否定するわけではないが、隠れた変数理論に拘る理由を否定する。