量子ポテンシャル理論
はじめに
ここでは量子力学の隠れた変数理論の一種である二重解の理論の派生形について紹介する。
デビッド・ボームの量子ポテンシャル理論
1952年、デビッド・ボームは、隠れた変数理論と題した論文で、ド・ブロイの理論を改良した量子ポテンシャル理論を示した。
ド・ブロイはさらに,先導方程式から(4.3)からただちに,2階の微分方程式(4.4)が得られることも示している. 形式的に言えば,この方程式はちょうどニュートンの運動方程式に,量子ポテンシャルといわれる項U(q,t)を付加したものである. ボームはのちにシュレーディンガー方程式から方程式(4.4)にいたるまでのド・ブロイの導出を再発見して,先導方程式(4.3)よりもむしろ方程式(4.4)を,粒子の運動に関する基本方程式とするアプローチを採用している. ボームのアプローチでは,先導方程式にしたがった粒子の運動を,さらにポテンシャルの影響,すなわち「力」の作用によって説明できるという利点がある. また、量子ポテンシャル項U(q,t)が無視できる場合には,まさにニュートンの運動方程式と一致するため,量子ポテンシャルの影響が量子現象に特有の奇妙さを生み出しているという理解が可能になる。
「量子という謎」(ISBN-10:4326700750,ISBN-13:978-4326700752,著:白井仁人・東克明・森田邦久・渡部鉄兵)P.113,114
(7)式のエネルギー表示に対応して,(11)式は,古典的なニュートンの運動方程式に,新たなポテンシャルQを追加した形になっている。 このように,エネルギー保存則においても運動方程式においても,ポテンシャルQの追加が,古典力学と「ボーム流の量子力学」を区別している。 このQを量子ポテンシャルと言う。
さて,ここまでの作業は,シュレーディンガー方程式の「近似」,あるいは「変形」というより,むしろ「拡張」である。 (8)式で与えられる量子ポテンシャルがどれほど奇妙に見えようとも,シュレーディンガー方程式から直接導きだされている以上,この理論の予想する実験結果は,標準的な量子力学と等価である。 この「拡張」が面白いのは,その解釈論であり,次のような主張が可能なところにある:従来の量子力学は,波動関数の振幅―実数部しか利用していないから,確率密度のような統計的物理量しか得られなかった。位相―虚数部も利用することで,古典力学のような運動学的な情報も得られるようになる。 これは意味深長と思う。 筆者自身,「波動関数の虚数部に注目せよ」というボームの考えには,はっとした。
ボームの理論の最大の特徴は,「粒子」である電子の軌跡が追跡できる点にある。
教育ノート1.波動関数のわかりやすい説明 - 日本女子大学紀要 理学部 第24号(2016)P.10,11
つまり、標準の量子力学では、Schrödinger方程式の虚数部しか用いておらず確率密度のような統計的物理量しか得ていない。 一方、量子ポテンシャル理論では実数部も積極的に利用しており、運動学的な情報も得ることが可能である。 ここで注意して欲しいのは、量子ポテンシャル理論はSchrödinger方程式から導き出されているので、この理論の予想する結果は標準の量子力学と同一ということである。
デビッド・ボームは、フォン・ノイマンのNO-GO定理は量子ポテンシャル理論には適用できないとした。
Bohmの測定の理論では問題の隠れた変数は観測される系の状態に依存するばかりでなく,また測定装置の状態にも依存するものと仮定された. そうした類の隠れた変数はVon Neumannによって考察されたことのないものである以上,Bohmとしては隠れた変数は量子力学と両立しないというVon Neumannの証明は使えないと主張することができた.
「量子力学の哲学 下」(ISBN-10:4314004274,ISBN-13:978-4314004275,著:マックスヤンマー,訳:井上健)P.340
ようするに、ノイマンのNO-GO定理では測定される系だけに依存する隠れた変数理論のみが否定されるので、測定装置にも依存する量子ポテンシャル理論は否定できないということである。 また、コッペン=シュペッカーのNO-GO定理も適用できないという。
関数関係B=f(A)にある物理量A,Bについて,測定値と所有値の平均が一致するというときには,次のことに注意しなければらならない。
<f(A)>S=<f(A)(q)>B≠<f(A(q))>B
一般に軌跡解釈では,Bの所有値はAの所有値に関数を適用した値とは異なりうる. すなわち,
B(q)=f(A)(q)≠f(A(q))
といことが起こりうる(付録B.2参照). したがって,コッペン=シュペッカーのNO-GO定理は適用されない。
「量子という謎」(ISBN-10:4326700750,ISBN-13:978-4326700752,著:白井仁人・東克明・森田邦久・渡部鉄兵)P.119,120
量子ポテンシャル理論には次のような批判もあったが、その批判に対応できるように修正されている。
量子ポテンシャル理論では、初期状態が不確定性原理に従う分布である場合には、終状態も不確定性原理に従う分布となることが分かっている。 逆に初期状態が不確定性原理に従わない分布の場合は、終状態でも従わないことになる。 この点についてはPauliらにより批判がなされた。 また最初の分布は、どのようにして不確定性原理に則った分布になったのだろうかという疑問も生じる。 この問題に対処すべく、Bohmらは揺らぎを持った流体の存在を仮定した修正版を提出した。 そして、量子と流体とのランダムな衝突に起因するBrown運動により、任意の量子の分布が不確定性原理に従う分布へと時間と共に移行することを示している。
後に Bohm が独自に提唱した量子ポテンシャル理論で、その批判は解決された。 そして、この理論 もPauliらにより批判され、更にBohmが回答したのは既に述べた通りである。 L. de Broglie はその後、“2 重解の理論”の研究を再開している。
量子ポテンシャル理論と確率力学 - 核データニュース,No.76(2003)P.42,47
二重スリット実験の真相で説明した通り、二重スリット実験における粒子の軌跡は次のようになる。
二重スリット実験に対する,電子の軌跡の計算結果を模式的に図2に示す。
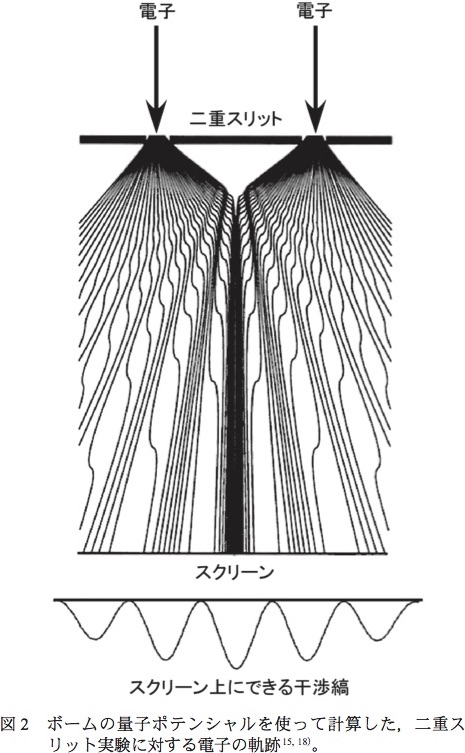
図2に示したように,スクリーンに到達した(多数の)電子の分布は,干渉縞を再現できる。注目すべきは,標準的な量子力学と違い,個々の電子は,古典的な粒子のように,明確に定められた軌道を通っていることである。 そして,どちらか一方のスリットだけを通過している。 ただし,電子の軌道は多数あるので,ある電子が「どの経路にのるか」は予言できない(←不確定性原理に対応している)。 ここには何の不明確さもない:すなわち,電子は粒子で,どちらか一方のスリットを通る。 干渉縞は量子ポテンシャルによる。
教育ノート1.波動関数のわかりやすい説明 - 日本女子大学紀要 理学部 第24号(2016)P.11,12
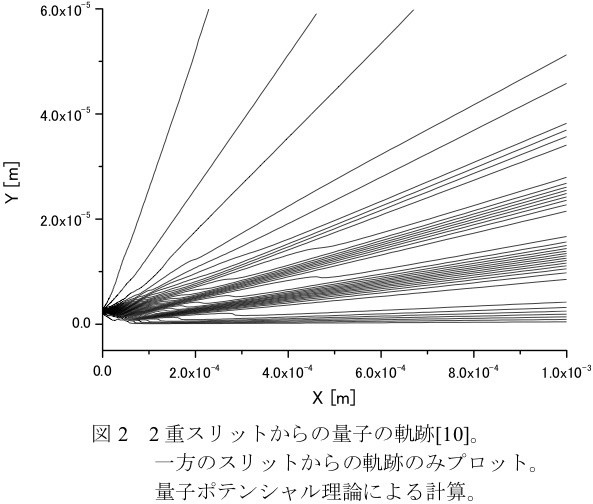
この量子ポテンシャルにより形成される量子の軌跡を図2に示す。 図2は、線源から見て左側のスリット一方のみからの軌跡である。 この図を折り返して2つ重ねると全干渉パターンが再現できる。 これから分かる最も驚くべきことは、左側のスリットを通過した量子はスクリーンの左側にしか到達しないことである。 これは2つのスリットの中央にある量子ポテンシャルの比較的大きなピークによる斥力のためと解釈され、標準の量子力学からは知り得ない事柄である。 量子ポテンシャル理論では標準の量子力学と異なり、量子は2重スリットのいずれか一方を必ず通過する。 この解釈上の違いは非常に大きい。 非局所的な量子ポテンシャルが2つのスリットの情報を量子に伝え、その結果として干渉が起こるのである。 ただ、量子ポテンシャル理論においても、通過したスリットを特定するために一方のスリット直後で量子を観測しようとすると干渉パターンは消失する。 なぜなら、検出器の設置と観測により量子ポテンシャルが大きく変化するためである。 それ故、量子ポテンシャル理論は標準の量子力学と矛盾をきたさないことになる。
量子ポテンシャル理論と確率力学 - 核データニュース,No.76(2003)P.39-40
量子トンネル効果については、次のように説明される。
1次元矩形ポテンシャルでのトンネル効果における量子の軌跡を、量子ポテンシャル理論で計算した例[11]について述べる。同一の条件で計算された標準の量子力学による結果は[12]にある。参考にされたい。
図4にはGauss波束上の各位置からの量子の軌跡を示している。図中、横軸が相対的な時間、縦軸が相対的な空間位置を示し0.5の位置が初期のGauss波束の中心位置となっている。 矩形ポテンシャルは0.72から0.78の範囲にある。 量子の初期位置が0.67より大きい場合、いわゆるトンネル効果を起こしていることが分かる。 これは2.2d)で説明したGauss波束自身による量子ポテンシャルによる量子の加速効果と、量子ポテンシャルと矩形ポテンシャルの相互作用により矩形ポテンシャルが低くなったことの2つの効果により理解される。 すなわち量子ポテンシャル理論では、量子は矩形ポテンシャルをトンネル効果によりしみ出て来るのではなく、量子ポテンシャルの効果により矩形ポテンシャルを乗り越えるのである。
量子ポテンシャル理論と確率力学 - 核データニュース,No.76(2003)P.40-41
量子ポテンシャル理論の課題が次のように指摘されている。
読者は,これほど面白いボームの理論が,どうして,標準的な量子力学で教えられないのかと疑問に思うかもしれない。 それには,いくつかの理由がある。
まず,第一に,キーアイテムである「量子ポテンシャル」の奇妙さが挙げられる。 通常のポテンシャルは,物体間の何らかの物理的な相互作用の結果として生ずる。 しかし,量子ポテンシャルには,それを生み出す相互作用がない。 量子ポテンシャルは,シュレーディンガー方程式を数学的に扱う中から出てきた量であり,電子(粒子)がそこにあるだけで発生する。 しかも,量子ポテンシャルを実験で観測することもできない。
第二に,束縛状態の電子状態に実験とあわない点がある。先に挙げた水素原子がよい例である。 ボームの理論では,1つの水素原子の電子は,どこかわからない場所で止まっている。 それならば,必ず,双極子モーメントが発生し,実験で観測できるはずである。 しかし,実際には,水素原子の双極子モーメントはゼロであり,水素原子中の電子は静止していないと結論される。
第三に,ボームの理論が与える最終的な計算結果(=実験と比較可能な結果)は,結局は通常の量子力学と同じものである。 電子の軌跡も,実際には,不確定性原理の制限を超えては,観測できない。 よって,電子の状態計算においては,ボームの理論は煩雑さを増やすだけのものである。
第四の,そしておそらく最大の理由が,ボームの理論が「非局所的な理論」だからである。
つまり,どんなに距離が離れていても,1つの電子に対する量子ポテンシャルは,もう1つの電子の変化に対し,いかなる媒体も経由しないで,瞬間的に(場合によっては光速を越えて!)反応することになる。 こうした「遠隔作用」は,多くの物理学者に忌避されるし,「光速を超える事は出来ない」という相対性理論とも衝突する。
以上のようにボームの理論を概観してみると,この理論は,「電子を粒子とみなす」という「わかりやすい」イメージを得る代償を(つまりは,電子の波動性を),量子ポテンシャルにおしつけたものと解釈できる。
ただし、「非局所的な理論」であることは、実験事実に整合させるために必要なことであり、同じ現象を扱う標準理論より劣っている理由にはなるまい。 それは、標準理論のように充足理由の法則を捨てるか、隠れた変数理論のように局所性の捨てるかの選択の違いでしかない。 むしろ、量子もつれの相関性を考慮すれば、充足理由の法則を捨てる方が遥かに不自然であろう。
また、計算上は「煩雑さを増やす」ことは、理論の真偽とは無関係であるし、正しい理論を否定する理由にもならない。 実用的な計算手段として簡単な計算式を採用することはあっても、計算が簡単な方を正しい理論とすることなどあり得ないのである。
さらに言えば、理論の背景部分についての「奇妙さ」、「実験で観測することもできない」性質も標準理論と何ら変わりがない。 標準理論も、奇妙な射影仮説を仮定しており、「それを生み出す相互作用」は説明されない。 これは「数学的に扱う中から出てきた」仮定であり、可観測量を測定するだけで発生する。 射影仮説適用後の可観測量は観測可能だが、射影仮説そのものを「実験で観測することもできない」。 以上を踏まえれば、標準理論と比べて唯一劣っている点は「束縛状態の電子状態に実験とあわない点がある」ことだけとなる。 この点は確率力学で解決される。
井元信之氏によれば、デビッド・ボームは可能性を提示しただけであって隠れた変数理論を強硬に主張したわけではない。
-後半生は、英国住まいでしたね。 本当に残念なことに、私がロンドンへの赴任で渡英する直前に亡くなりました。 井元さんは、ボームにあったことがおありでしたね。
ええ、そうなのです。 ボームに会ったとき、私は「『ボーム解釈』をご自身はどう考えているのか」と聞いたことがあります。
-ボームは何と答えたのですか。
「この解釈は一つの仮説であって、私は正しいと言っているわけではない。 科学というものは仮説を立てないと進歩しないだろう」と言っていました。
「SF小説がリアルになる 量子の新時代」(ISBN-10:4022732873,ISBN−13:978-4022732873,著:佐藤文隆/井元信之/尾関章)kindle版p.173-174
尚、かつて、井元信之氏は「相対論を満たさない」という理由で量子ポテンシャル理論を否定していた。
私自身は、他にもノーベル賞級の功績のあるボームのことをすごく尊敬しています。 しかし、ボームの解釈は、あまりに信じることができないというのが正直なところです。 相対論を満たさないという点が受け入れられない。
「SF小説がリアルになる 量子の新時代」(ISBN-10:4022732873,ISBN−13:978-4022732873,著:佐藤文隆/井元信之/尾関章)kindle版p.174
尚、その後、井元信之氏は次のように態度を改めている。
その後、私は「Bohmの理論」すなわち「非局所隠れた変数の理論」を「問答無用」とまで拒絶することはなくなった。
その理由について次のように説明されている。
この意味で、ブラックボックスの中では実在としての変数RやSが非局所的に動き回るモデルである。
もちろんブラックボックスの外にいる我々は、その応答を利用して超光速通信をすることはできない。
「非局所性」の意味:
Bohmの量子ポテンシャルの非局所性とは、「ブラックボックスの中で超高速で伝わる」ことを意味。
「影響が空間を連続的に伝わる」意の局所性は、ブラックボックスの外からのaccessibleなものの性質。
常識で考えて、真っ当な科学者であれば「相対論を満たさないという点」を受け入れるようになった、すなわち、相対性理論を否定するようになったとは考えにくい。 よって、これは、局所性の制限はブラックボックスの外からのaccessible(アクセス可能)な現象のみに適用されるのであって、ブラックボックスの外からのaccessible(アクセス可能)でない所で非局所性が現れても相対性理論には反しないという意味である。 これは、事象の水平面内のような現実的に問題にならない所で物理法則が破綻する特異点があっても問題ないのと同じであろう。
総合案内
科学一般
疑似科学等
- 疑似科学
- 数学や科学への無理解
- 疑似科学を批判する疑似科学
- STAP細胞論文捏造事件
- CCS地震原因説
- 地球温暖化懐疑論
- 疑似科学者列伝