波動性と粒子性の二重性

• 物質波
• 問題点整理
• 解決策
  • 隠れた変数理論の可能性
  • 測定の物理的定義
• よくある誤解

物質波 

量子力学では、波動性と粒子性の二重性が議論される。 ルイ・ド・ブロイは、アインシュタインの光量子仮説を元に、粒子にも波動性があるのではないかと考えた。 その後、電子が波動性を示すことは電子線の回折実験で実証された。 アインシュタインの論文を通じてルイ・ド・ブロイの物質波の概念を知ったシュレーディンガーは、その波の振る舞いをシュレーディンガー方程式として定式化し、波動力学を提唱した。 波動力学では、ボーアやゾンマーフェルトの量子条件は、原子核の周りに定在波ができるケースとして説明できる。 シュレーディンガーは、論文「ハイゼンベルグ-ボルン-ヨルダン-の量子力学と私の力学との関係について」において、行列力学と波動力学が数学的に等価であることを証明した。

問題点整理 

粒子と波の二重性とは何か？

	身近な例	どう数える?	どこにいる?	入口がいくつもあったら?
粒子	小石,ボール	1個、2個・・・	空間の1点に局在している	どれかひとつだけ通る
波	水の波,音,電磁波	個数は数えられない。強さはある	空間に拡がっている	全部通り、合流すると重なり合う

初めて学ぶ物理学 量子論 by 筑波大学物理学系素粒子理論研究室金谷和至教授

なお、授業中は述べなかったが、シュレーディンガーがシュレーディンガー方程式を世に出した時、すでに水素原子の回りにある電子について計算しているのだが、この電子の存在確率も古典的には行くことができない場所まで広がっている（確率は小さいが）。 もっともシュレーディンガー本人は「確率が広がっている」とは考えていなかった。

量子力学講義録2005年第８回 - 琉球大学理学部物質地球科学科准教授前野昌弘の講義録

重要な２つの性質を抜き出す。

	量	大きさ
粒子	分割可能な最小単位を持つ（量子性）	ある一定以下の大きさを持つ（局在性）
波	いくらでも細かく分けられる（連続性）	任意に大きさを変えられる

粒子には、波と違って、量的な制限と大きさの制限がある。 このうち、量的な制限の違いはあまり問題視されなかった。 光子の量子性は、量子力学の標準理論に反発したアインシュタインが発表した理論である。 多くの物理学者が問題としたのは大きさの制限の違いである。

１点に集約される性質と、空間的な広がりを持つ性質が両立する…とは、何とも奇妙な話である。 クリントン・デイヴィソンらは、電子線の回折実験で電子に波とての性質があることを証明した。 しかし、その波としての性質が最小単位の量子でも生じることまでは証明されていなかった。 であれば、複数の粒子であれば、１つ１つは１点に集約されていても、その集合体でなら空間的な広がりを構成できるのではないか。 とはいえ、波動力学で原子モデルを説明するためには、最小単位の量子でも波としての性質が必要になる。 また、光については最小単位の量子でも波の性質を示すと考えられていた。

問題は、波のような性質をもたらすほど光子の数は多くないことである。

---

つまり、ある一瞬には、室内の光子数は10の12乗個程度しかない。 これは、１立方ミリメートル当たり10個程度ということであり、空気分子が10の16乗個程度であるのと大きな違いである。

「量子力学の解釈問題―実験が示唆する『多世界』の実在」(ISBN-10:4062576007,ISBN-13:978-4062576000,著:ColinBruce,訳＆注:和田純夫)P.35

空気分子の数と比べて論じるのは乱暴なので、もう少し補足説明する。 「１立方ミリメートル当たり10個程度」を単純計算すると、光子と光子の平均間隔は0.46mmくらいであろうか。 それに対して、可視光線で最も長い波長は約800nmである。 以上により、この場合の光子と光子の平均間隔は波長の５７５倍となる。 常識で考えれば、複数の粒子が波を形作るなら、粒子と粒子の平均間隔は波長よりかなり短くなければならないはずである。 しかし、実際の光子と光子の平均間隔は波長の５００倍以上も開いている。 これでは、複数の粒子が波を形作るとは考えにくい。

このように、かなり以前から、複数の粒子で波が形作られるとする考えは否定されていたようだ。 そして、それは、二重スリット実験の真相で説明した通り、単一電子による二重スリット実験（1974年）で実証された。

たった１個分で、１点に集約される性質と、空間的な広がりを持つ性質を併せ持つのは不思議な現象である。 シュレーディンガーは、波が物質の実態であるという波動一元論の立場をとり、粒子として観測されるものは一点に凝集した波であって、凝集した状態を持続的に維持可能であるとした。 波動関数でも、ある瞬間のみ一点に凝縮した波を記述することは可能だ。 しかし、ハイゼンベルクの論文「量子論的運動学および力学の直観的内容について」において、凝集した波は時間とともに広がってしまうことが明らかにされている。 一点に凝縮した波もその時刻の前後では広がりを持つ。 結果、測定のタイミングに合わせて一点に凝縮する波を作ろうとしても、辻褄を合わせることができない。 そんな都合の良い変化が測定の瞬間にだけ起きる原因を説明できない。 ボルンは解決策として確率解釈を提唱した。 それは、今日の標準理論では、極めて乱暴な確率的手法である射影仮説として導入されている。 標準理論に対して、次のように主張する者もいる。

• 波動関数は確率の波であって存在しない
• 多数の粒子の可能性が重なり合って存在している

しかし、それは標準理論ではない。 標準理論での扱いは次のとおりである。

• 波動関数は確率を表すが、その正体については問わない
• 可観測量は測定時に決定するが、過程の粒子性については問わない

標準理論においては、過程について言及しない行列力学の作法が維持されており、結果を確率的に求めることしかできない。 意外に思われるかもしれないが、量子力学の標準理論は過程の現象である波動性も粒子性も考慮していないのである。 波動性に見える数式は、計算方法として用意しているだけであって、それが現象としての波動性を示しているかどうかについて標準理論は一切言及しない。 また、粒子性に見える結果についても、計算結果として示しているだけであって、それが粒子性によってもたらされた性質であるかどうかについて標準理論は一切言及しない。 ただ、現実には、波動性や粒子性と解釈できる現象が推測され、それは標準理論の数学的枠組みとも矛盾しないため、量子力学では波動性や粒子性について言及される。 しかし、波動性や粒子性は標準理論の概念には含まれていないので、波動性や粒子性に言及した時点で標準理論とは呼べなくなる。 もちろん、標準理論は量子の波動性や粒子性を否定しているわけでもない。 しかし、波動性や粒子性に言及すると、それは標準理論の外側に一歩踏み出した話となる。 ようするに標準理論の言っていることは「数学的にはこうなりますが現実の現象がどうなっているかは知ったこっちゃありません」である。 そして、過程の現象について実証された理論も現存せず、また、過程の現象を実証することも原理的に不可能である。 標準理論に関して可能性のある解釈として過程の現象に言及することが関の山であるため、過程の現象に言及したものは量子力学の解釈と呼ばれる。

では、標準理論から一歩進んで、個々の解釈としてそれぞれの実在を論じるとどうか。 まず、波動性については、ハイゼンベルクの示した考えのように、「波動関数を粒子の誘導場(Führungsfeld)と解釈」することは波の実在性を否定することにはならない。 二重スリット実験(正確かつ素人向け説明)で説明した通り、二重スリット実験では、単一の粒子の持つ波どうしが干渉を起こしている。 このことは、波が単なる存在確率を示す概念に留まらないことを示している。 言い換えると、存在確率という概念が波を作り出しているのではなく、確率規則が波を存在確率と見なす概念なのである。 ようするに、波そのものは存在確率以外の何かなのである。 ただ、波と粒子との関係を論じるときには存在確率にだけ着目しようと言ってるだけなのだ。

粒子については、数式上では、多数の粒子の可能性が重なり合った状態を記述している。 しかし、標準理論は、その正体については問わない立場である。 そして、それが正体を正確に記述しているのかどうかは諸説あろう。 標準理論と数学的に等価な理論において単一の粒子の実在を想定する理論もある。

解決策 

隠れた変数理論の可能性 

隠れた変数理論の具体例として、ド・ブロイが1927年のソルベー会議で提案した二重解の理論がある。 それならば二重スリット実験の結果も問題なく説明できる。 しかし、困ったことに隠れた変数理論には解決すべき課題が多い。 課題を解決しようと理論を修正すると、あまりに非常識すぎる珍説になってしまう。 今日でも、隠れた変数理論は完全には否定されていないが、かなり実現が困難な理論となっている。

測定の物理的定義 

ようは、射影仮説の核となる測定を物理的に定義できれば良い。 そうすれば、マクロ世界の法則と量子力学の間に矛盾は生じない。 それでも量子力学の不可思議さは残るが、ミクロの世界が我々の常識と違っていても主観的に気持ち悪いこと以外には何ら不都合はない。

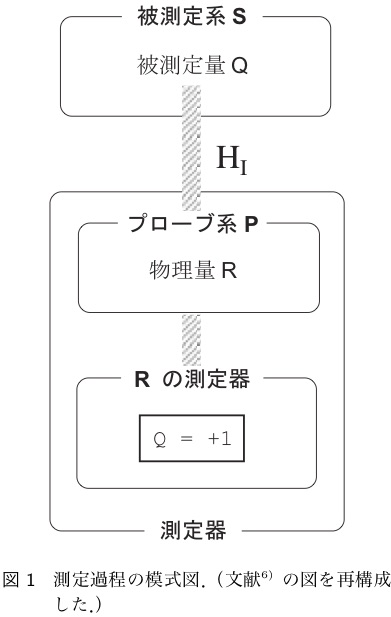
図1のように，被測定系Sのある物理量Qを測る場合，Sを測定器の一部(プローブ系Pと呼ぶことにする)と相互作用させ，Qの情報を，Pのある物理量Rに「コピー」してくる. ここで，「コピー」と言ったのは，Qの値とRの値が相関するようにする，という意味であり，そっくり写し取るなら理想的だが，そうでなくても，何か関連付けば良い. そして，測定器の中には，このRの値を測る部分が付いている.Rの値は，Qの値と相関しているので，このRの値からQの値を推定することができる. その推定の仕方は，測定器の構造により決まるが，Rの測定値から，その推定のルールにのっとって求めたQの推定値を，ディスプレイとか目盛りとかに表示するのが測定器の動作原理である.

このように分解して考えると，Rを測る過程は理想測定と見なせるので，射影仮説が使える.(逆に言えば，公理より，理想測定と見なせる過程が存在するので，Rの測定が理想測定になるようにPを選ぶ!) つまり,理想測定と見なせる境目までは,量子論に従う系の一部として扱い,そこから先を考えることは,射影仮説により遮断する. それが,一般の測定過程の分析の仕方の処方箋である. この境目(「Heisenberg cut」と呼ばれる)の位置には任意性があるが,先の方にずらす分には,まったく同じ結果を与えるので,要するに,充分に大きな系を量子論に従う系として扱っておけば,結果には任意性は出ないのである.

量子測定の原理とその問題点 by 東京大学大学院総合文化研究科広域科学専攻相関基礎科学系＆東京大学大学院理学系研究科物理学専攻：清水明教授

ミクロとマクロの間に明確な境界を設けようとすると、例外を定義できない。 しかし、ミクロからマクロへ性質が連続的に変化すると考えれば、ミクロとマクロの干渉で例外を難なく定義できる。 ある程度、マクロ的な性質が強く現れる所よりも観測者側に近い所にはHeisenberg cutを設けることができる。

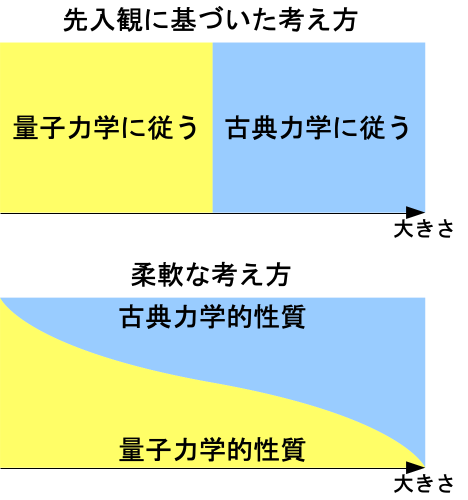
Heisenberg cutより観測者側は、観測対象に一定の影響を与えるものの、その影響は非常に小さいのでほとんど無視できる。 シュレーディンガーの猫の思考実験についても、量子測定理論では次のように解釈される。

以上のことから，射影公準によれば，波束の収束は放射性物質とガイガーカウンター（の一部）の相互作用が終了する時刻にはすでに起こっており，この時刻で猫の運命は決まる． この観点からは，巨視的な猫の状態がどのように変化するのかは，測定終了後にどのような増幅過程が進行するのかという技術的な事柄にすぎない．

「量子という謎」(ISBN-10:4326700750,ISBN-13:978-4326700752,著:白井仁人・東克明・森田邦久・渡部鉄兵)P.15

量子デコヒーレンス等でも同様の説明は可能である。 ミクロからマクロへの連続的変化が否定されない限り、例外の定義に「知性ある存在の意識」が必要ない事実だけは揺るがない。

よくある誤解 

トンデモ事例の解説は波動性と粒子性の二重性トンデモ解説に移動した。