遅延選択量子消しゴム実験トンデモ解説
最初に
このページは遅延選択量子消しゴム実験に対して、科学的に明らかに誤ったトンデモ解説を紹介するものである。 当サイトの科学項目の目的も参照のこと。
科学で扱える現象の範囲
科学で扱うためには、同じ条件では同じ現象になる(同じ数式で記述できる)ことが必須の前提となる。 その前提が崩れれば、科学法則が成立しないし、実験の再現性も失われる。 よって、科学法則を見出したり、実験で結果を確かめるためには、この前提が崩れてはならない。 言い換えると、同じ現象にならない(同じ数式で記述できない)ケースを科学で扱うためには両者には違う条件が必要となる。 尚、量子力学は確率的に結果を推定する理論であるので、ここで言う「現象」には確率も含む。
オッカムの剃刀
実験結果を説明するために不要な仮定は置かない。 必要のない仮定を置いても、理論的考察の役にたたない。 無駄に話を難しくすれば、間違いを生みやすくなる。 メリットが全くなく、かつ、デメリットしかない不要な仮定は可能な限り排除すべきだろう。
誤った説明の例
以下に紹介するサイト、標準理論に関する説明はともかく、こと解釈系に関しては根拠のない唐突な仮定を何の説明もなく置いて、あたかも、それが当然の暗黙の了解であるかのように偽装している。 この手の解釈系トンデモは珍しくなく、標準理論と独自解釈をゴッチャにして語る傾向があるが、このサイトはまだマシな方かもしれない。
二重スリットを使った干渉実験では、粒子がどちらのスリットを通ったかを特定するような観測を行うとその時点で波の性質が消えてしまい、干渉が起こらなくなってしまう。
二重スリット実験の真相で説明したとおり、「二重スリット実験を使った干渉実験」において、「粒子がどちらのスリットを通ったかを特定するような観測を行う」ことによって「波の性質が消えてしま」うとする証拠は何もない。 確かに、干渉縞は生じなくなるが、それは、「干渉が起こらなくなってしま」ったことを意味しない。 むしろ、干渉縞が生じないような干渉が起きていると考えないと理論と整合しない。
ところが、観測そのものが問題なのではないのではないかという可能性が出て来た。 観測を行った後でその結果が分からないように消してしまうような仕組みを導入すると、なんと、干渉縞が復活させられることがあるというのである。 一度記録したはずの観測結果を、あたかも消しゴムで消すように、「分からないようにする」「なかったことにする」というような意味である。
既に説明した通り、「A Delayed Choice Quantum Eraser」では、「観測を行った後でその結果が分からないように消してしまうような仕組みを導入」していない。 そして、「干渉縞が復活させられる」のは「粒子がどちらのスリットを通ったかを特定するような観測を行」っていないケースに限られる。 「粒子がどちらのスリットを通ったかを特定するような観測を行う」ための下準備を行なっているが、それだけでは「粒子がどちらのスリットを通ったかを特定するような観測を行」うことはできない。 そして、「粒子がどちらのスリットを通ったかを特定するような観測を行う」機会を放棄した場合に限って、それとは別の情報に基づいて「干渉縞が復活させられる」だけである。 つまり、「干渉縞が復活させられる」場合は、「一度記録」などしていないのだから、存在しない「観測結果」を「あたかも消しゴムで消す」ことは不可能である。 既に手に入れたものを失うのではなく、手に入れる準備だけして手に入れる前に入手機会を放棄するのだから、量子消しゴム(quantum eraser)という表現は実態から遠くかけ離れている。 量子断念(quantum abandoner)や量子機会損失(Quantum opportunity loser)とでも表現すれば実態に沿った極めて正確な表現となろう。
また、後で説明するが、この実験では、「粒子がどちらのスリットを通ったかを特定するような観測」を断念する「仕組みを導入」しただけでは「干渉縞が復活」しない。 この実験で「干渉縞が復活させられる」のは、相殺された複数の干渉縞のうちの1つを取り出すことによって実現している。 そして、それは、干渉縞の相殺によって隠れされてはいたものの、その影で干渉が起きていたことを示している。 ただし、この実験では、相殺された複数の干渉縞のうちの1つを取り出すために、観測を断念する「仕組みを導入」が必要となる。
繰り返すが、「観測を行った後でその結果が分からないように消してしま」っては、干渉縞のうちの1つを取り出すための情報を得ることができない。 「観測を行っ」ってしまっては、必要な情報が消失してしまい、その後で「その結果が分からないように消して」も完全に手遅れである。
この実験では実に巧妙に、精密にセッティングがされており、D₁やD₂には光は二つのスリットの両方のコースで同時に届いたのだと言えるようになっている。 つまり、こちらへは光は波として到達するのである。 なぜそんなことが言えるかと言うと、これは実に職人技なのだが、波長レベルの精度での微調整が行われており、D₁には二つの波が強め合うように、D₂には二つの波が弱め合うように配置されているのである。 つまり、D₁には必ず光は来るが、D₂には光が来ないようになっている。 これは波の性質がないと出来ない芸当だ。
D₁やD₂に「こちらへは光は波として到達する」という説明では、あたかもD₃やD₄には「光は波として到達」しないかのように聞こえる。 しかし、D₃やD₄には「光は波として到達」しないと考える理由が何もない。
その結果として何が分かったか。 例えば、D₃で検出されたときのデータだけを集めてスクリーン上での光子の検出がどのように分布したかをグラフにしてやると、まるでそこに最初から一つの粒子しか飛んでこなかったような、中心付近にピークを持つ分布になる。 D₄の場合も同じ。
ところが、D₁の場合を調べてやるとちゃんと干渉が起きていたかのような分布になっているのである。 D₂の場合にも同様に干渉は起きているようだが分布が逆になる。 D₂で検出される確率が上がるのは片方の位相が逆転しているときなのだからそれ自体は不思議ではない。
こんな無茶な実験をしたにもかかわらず、干渉は起きていたのだ。 スリットのどちらを通ったかを特定できるような観測結果を得たときには単独の粒子のように振る舞っており、それを分からないように消してしまうような観測をしたときには干渉縞が作られるように振る舞っていたのである。 全体を集めれば実際に干渉が起きていたわけではないような振る舞いをしていたのだが、後から集計したデータと突き合わせればそうなっていたことが分かるわけだ。
光子のペアの一方は他方の光子の観測結果がどうなるかをどうやって知ったというのだろう。 知った上で行動を変えたのだろうか? だめだ、不思議すぎてこの先の説明ができない。
「中心付近にピークを持つ分布」は論文のFIG. 5を指している。
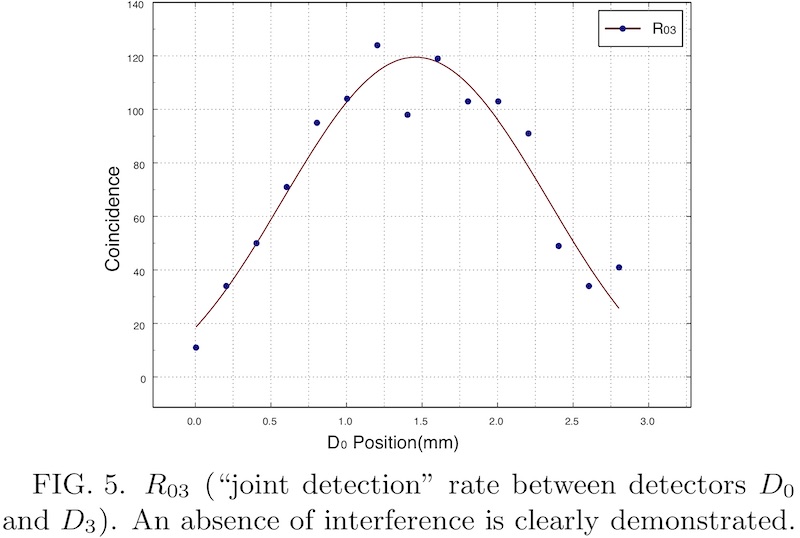
一箇所に集中した分布であれば、「最初から一つの粒子しか飛んでこなかったような」という推測は成立し得るかもしれない。 しかし、この図のような広がりを持つ分布からは「最初から一つの粒子しか飛んでこなかったような」という推測は全く成立しない' よって、「単独の粒子のように振る舞って」いるとする証拠は何もない。 むしろ、この横に広がった結果は、回折による空間的広がりにより、「単独の粒子のように振る舞って」いないことを示唆するものである。 百歩譲って、このようなパターンが「単独の粒子のように振る舞って」いることを示すなら、同様のパターンとなるR₀₁+R₀₂においても「単独の粒子のように振る舞って」いることになる。 しかし、そうすると、R₀₁とR₀₂に分離したときに干渉縞が復活することが説明できない。 よって、実験結果と整合するように考察するならば、このようなパターンが「単独の粒子のように振る舞って」いることを示さないと考える必要がある。
科学で扱うためには、【同じ条件では同じ現象になる(同じ数式で記述できる)こと】が必須の前提となる。 何故なら、同じ条件で同じ現象にならない(同じ数式で記述できない)のでは、法則を立てることができないので、科学で扱うことはできないからである。 この実験においては、下側経路(D₁〜D₄に到達する経路)における測定や操作が、上側経路(D₀に到達する経路)の結果に影響を与えると考える理由が全くない。 というのも、下側経路における測定や操作が、上側経路の結果に影響を与えていないと考えても、何の問題もなく実験結果が説明できるからである。 むしろ、下側経路における測定や操作が、上側経路の結果に影響を与えていると考えると、直近の段落で説明したような致命的な矛盾が生じる。 よって、科学に必須の前提である【同じ条件では同じ現象になる(同じ数式で記述できる)こと】を疑う必要が全くない。 それなのに、何故、一方は「単独の粒子のように振る舞って」いると考え、他方は「干渉縞が作られるように振る舞って」いると考えるように、同じ条件で違う現象になると考えるのか、その理由が何一つ示されていない。 科学に必須の前提を何の理由もなく崩すのでは、科学とは到底呼べない非科学的な考察であろう。
原論文でも次のように任意の計数率R₀ⱼが波動関数で計算できることを明記している(R₀ᵢは誤記であると思われる)。
To explain the experimental results, a standard quan- tum mechanical calculation is presented in the following. The “joint detection” counting rate, R₀ᵢ, of detector D₀ and detector Dⱼ, on the time interval T, is given by the Glauber formula [8]:
実験結果を説明するために、標準的な量子力学計算を以下に示す。 時間間隔Tにおける検出器D₀と検出器Dⱼの「相関検出」計数率R₀ᵢは、以下のGlauberの式[8]で与えられる。
R₀ⱼ∝1/T∫₀ᵀ∫₀ᵀdT₀dTⱼ<Ψ|E₀⁽⁻⁾Eⱼ⁽⁻⁾Eⱼ⁽⁺⁾E₀⁽⁺⁾|Ψ> =1/T∫₀ᵀ∫₀ᵀdT₀dTⱼ|<0|Eⱼ⁽⁺⁾E₀⁽⁺⁾|Ψ>|² ,(1)
波動関数で計算するということは、波動性があることを想定しているということである。
干渉縞の有無と干渉の有無が全て完全に一致するのであれば、この結果が「不思議すぎ」ることは言うまでもない。 であれば、この結果が示すことは、干渉縞の有無と干渉の有無が一致しないことを示していることは明らかである。 干渉縞の有無と干渉の有無が一致しないことを前提にしないと「D₂で検出される確率が上がるのは片方の位相が逆転しているときなのだからそれ自体は不思議ではない」という考察が生まれてくる余地もない。 「スリットのどちらを通ったかを特定できるような観測結果を得たとき」は、「分布が逆」の2種類の干渉縞を分離できないために、双方が相殺された結果として干渉縞が見えなくなっているだけなのである。 逆に、「それを分からないように消してしまうような観測をしたとき」(表現の不正確さは既に説明済み)は「分布が逆」の2種類の干渉縞を分離できるために、「分布が逆」の2種類の干渉縞の両方を見ることができるようになる。 だから、この結果を説明するうえで「光子のペアの一方」が「他方の光子の観測結果がどうなるか」を「知った上で行動を変え」る必要は全くない。
尚、先ほども説明した通り、「それを分からないように消してしまうような観測をしたとき」は表現として不正確である。 この実験で「消してしま」っているのは「スリットのどちらを通ったかを特定できるような観測結果」ではない。 干渉縞が得られるときは、「スリットのどちらを通ったかを特定できるような観測結果」を最初から入手していないのであり、存在しない情報を「それを分からないように消してしまう」ことはできない。
そもそも、「光子のペアの一方」が「他方の光子の観測結果がどうなる」を「知った上で行動を変え」たとしても、干渉縞の有無と干渉の有無が完全に一致するのであれば、R₀₁(D₀の検出結果のうちD₁と相関する結果のみを抽出したもの)+R₀₂(D₀の検出結果のうちD₂と相関する結果のみを抽出したもの)では干渉縞が生じないにも関わらず、R₀₁とR₀₂を分離すると「干渉縞が作られる」ことを説明できなくなる。
遅延選択量子消しゴム実験で解説している通り、奇妙な仮定を置かずとも、この実験結果は何ら矛盾なく説明できる。
レーザー光源から放たれた瞬間から、電磁波のような何かが確率の波として伝わってきている。 スリットの間の壁に当たって通り抜けられなかった可能性、一方の穴から通過した可能性、他方の穴から通過した可能性。 それら全てが、粒子としてどこかで観測される瞬間まで広がり続ける。 粒子が観測されればその全てが消える。
スリットのそれぞれの隙間を通り抜けた可能性の波はそれぞれのコースを進み、それぞれが二つの光子を発生させる可能性へと引き継がれる。 この段階ではまだスリットの一方を通った波と他方を通った波との干渉は起きていない。 お互いに離れたコースを通過しているから干渉を起こしようがないのである。
既に説明した通り、この実験結果を説明するために「確率の波」だとか「可能性の波」などというわけのわからないものを想定する必要は全くない。
このように量子力学の標準的な考え方を使えば説明に困るところがない。 いつもの量子力学であり、あっけないくらいだ。 少しばかり不思議なのはペアで生成された光子の状態である。 それらについての確率の波は不可分で一体であり、互いにどんなに距離が離れていても、一方を観測して何らかの結果を得るということは他方を観測したことと全く同じだと言えるのである。 先ほど注意書きとして、今回のペアの光子はエンタングル光としてよく利用される重要な性質を失っていると書いたが、それでも広い意味での量子もつれ状態(エンタングル状態)にあるとは言えるだろう。
どれか一つの可能性を観測した瞬間に他の全ての可能性の波が消えてしまうというのが不自然すぎると感じるのなら、多世界解釈的なイメージが助けになるだろう。 自分は観測によって一つの可能性と結びついてしまって他の可能性を認識できなくなっただけであり、他の可能性を引き当てた別の自分との重ね合わせ状態に移行したのである。 そういう解釈も可能だと言うだけで、実際にそうなっているかどうかを確認することはまだできていない。
この実験結果を説明するために必要なことは、量子もつれのペアの初期位相が同期していることだけである。 ペア間の初期位相差が常に定数(必ずしも0である必要はない)でありさえすれば、この実験の結果は何ら矛盾なく説明できる。 「量子力学の標準的な考え方」(後述するが、これは量子力学の標準理論ではない)を使わなくても、「説明に困るところがない」ことは言うまでもない。 「多世界解釈的なイメージ」も全く不要である。
言い換えると、説明が必要なことは、唯一、量子もつれのペアの初期位相が同期していることだけである。 ペア間の初期位相差が常に定数(必ずしも0である必要はない)であるという関係性が示せれば、この実験結果は何ら矛盾なく説明できる。 しかし、この関係性が崩れるなら、この実験結果はどうやっても説明できない。
尚、ここで「量子力学の標準的な考え方」とされているものは量子力学の標準理論ではない。 何故なら、量子力学の標準理論は過程を数式で記述していても、その数式がどのような物理的過程を示しているかについては言及しないからである。 だから、物理的過程に言及してしまえば、量子力学の標準理論から逸脱することになる。 標準理論において「確率の波」や「可能性の波」は数式上の扱いであって、それを物理的過程とする考えを「量子力学の標準的な考え方」として紹介すると疑似科学の類になろう。 「確率の波」や「可能性の波」を物理的過程と考える物理学者がいないわけではないが、その考えに大多数の物理学者が合意しているわけではない。
従来の量子力学の解釈の範囲で説明できてしまうのならば、この実験の意義はどこにあるだろうか? 二重スリット実験で粒子の経路を確認するような観測を行うと干渉が起こらなくなるのは、観測という行為によって状態が乱されてしまうからだと、我々は古くからそういう説明をしてきた。 ところが本質はそこではなかったのである。 今回の実験では、観測を行うことで干渉が消えてしまったように見える。 しかし後に得られる情報次第で、干渉が起こっていた事実を掘り起こすことができるというのである。
既に説明した通り、「二重スリット実験で粒子の経路を確認するような観測を行う」場合に、「干渉が消えてしまったように見える」が、それは「干渉が起こらなくなる」のではなく、「干渉が起こっていた事実」があるにも関わらず干渉が見えなくなるだけである。 そうでなければ、理論とも整合しないし、この実験の結果も説明できない。
そして、この実験においても、干渉縞が消えることは「観測という行為によって状態が乱されてしまう」せいであることには変わりがない。 この実験では「観測という行為」によって位相が乱されるのである。 しかし、この実験では、移相差別の結果を選別できるため、「干渉が起こっていた事実を掘り起こすことができる」のである。 この実験では、経路情報と移相差選別のための情報は、どちらか一方しか得られないという相補性が成立している。 しかし、この実験だけでは、相補性が必然的なのか偶然なのかまではわからない。 もしも、位相を乱すことなく量子もつれのペアを作ることが可能なら、通過スリットを特定しながら干渉縞を作ることも可能になる。 逆に、相補性が量子力学の根源的原理であるなら、当然、位相を乱すことなく量子もつれのペアを作ることは不可能となる。
この実験と同様に、「観測という行為」によって運動量が乱される場合も、「干渉が起こっていた事実」があるにも関わらず干渉縞が見えなくなるだけと推測できる。 そして、運動量選別が可能なら、「干渉が起こっていた事実を掘り起こすことができる」はずである。 今日において「干渉が起こっていた事実を掘り起こすこと」に成功していないのは、運動量選別の具体的方法が発見されていないだけなのである。 よって、この実験から「本質」は「観測という行為によって状態が乱されてしまう」こと「ではなかった」とは到底言えない。 もちろん、運動量選別が可能であったとしても、そのために経路情報を断念しなければならない可能性は否定できない。
一般論化すれば、経路測定を可能にする「観測という行為」によって、必ず、測定対象の何かが擾乱される。 何が擾乱されるかは、測定方法によって様々であるが、経路を特定する限り、干渉縞が成立するための必須条件が必ず擾乱される。 その結果、経路測定と干渉縞が両立しなくなる。 それが、相補性原理の本質である。 不確定性原理は、相補性原理が位置や運動量に影響するケースのみを考慮した原理に過ぎないのである。 不確定性原理よりも相補性原理がより根源的な原理であるという意味で【「粒子の経路を確認するような観測を行うと干渉が起こらなくなる」のは「観測という行為によって」位置や運動量が乱されてしまうからではない】と説明されることがある。 しかし、それは乱される対象が位置や運動量に限らないことを示しているだけであって、「状態が乱されてしまうから」ではないとの意味ではない。
この実験は、「観測という行為によって状態が乱されてしまう」事例において、その擾乱を後から補正できる場合は、干渉縞が取り出せることを示している。 干渉縞が取り出せるということは、干渉が起こっていることを示していており、それは波動性が失われていないことを意味する。 ようするに、「観測という行為によって状態が乱されてしまう」事例においても、量子の波動性は失われず、干渉自体は発生している(相殺されるので干渉縞は見えない)ことを示唆している。 つまり、この実験が示すことは「粒子がどちらのスリットを通ったかを特定するような観測を行うとその時点で波の性質が消えてしまい、干渉が起こらなくなってしまう」という考察の誤りである。 「本質はそこではなかった」の「そこ」は、干渉縞が生じないことをもって、干渉がないと考え、波動性が失われたと考えることである。 この実験が示す真実は「粒子がどちらのスリットを通ったかを特定するような観測を行」っても「その時点で波の性質が消えてしま」うことはなく、「干渉が起こらなくなってしまう」こともないが、相殺されて干渉縞は見えなくなることである。
総合案内
科学一般
疑似科学等
- 疑似科学
- 数学や科学への無理解
- 疑似科学を批判する疑似科学
- STAP細胞論文捏造事件
- CCS地震原因説
- 地球温暖化懐疑論
- 疑似科学者列伝