二重スリット量子消しゴム実験

別の実験
前置き
- 科学で扱える現象の範囲
- オッカムの剃刀
基本原理
Double-slit quantum eraser（量子消しゴム実験）
- 実験セットの説明
誤った説明の例

別の実験

別の方法による量子消しゴム実験を遅延選択量子消しゴム実験で紹介する。

前置き

手っ取り早く結果を知りたい方は以下にどうぞ。

科学で扱える現象の範囲

科学で扱うためには、同じ条件では同じ現象になる(同じ数式で記述できる)ことが必須の前提となる。 その前提が崩れれば、科学法則が成立しないし、実験の再現性も失われる。よって、科学法則を見出したり、実験で結果を確かめるためには、この前提が崩れてはならない。言い換えると、同じ現象にならない(同じ数式で記述できない)ケースを科学で扱うためには両者には違う条件が必要となる。尚、量子力学は確率的に結果を推定する理論であるので、ここで言う「現象」には確率も含む。

オッカムの剃刀

実験結果を説明するために不要な仮定は置かない。必要のない仮定を置いても、理論的考察の役にたたない。無駄に話を難しくすれば、間違いを生みやすくなる。メリットが全くなく、かつ、デメリットしかない不要な仮定は可能な限り排除すべきだろう。

基本原理

二重スリット実験の真相で説明した二重スリット実験において、スリット通過時は経路印(which path marker)のみを付加してスクリーン直前で経路情報(which path information)を検出する方式、および、経路印を消去して通常の二重スリット実験に戻す原理について説明する。

尚、量子消しゴム(quantum eraser)とは、非常に誤解を招く言い回しである。事実、ネット上には「経路情報(which path information)を後から消せば、干渉縞が復活する」という実験事実に反した言説が多く見られる。この実験で消しているものは、どちらのスリットを通過したかの情報＝経路情報(which path information)ではなく、それを測定するための目印となる情報＝経路印(which path marker)に過ぎない。 この実験では、可逆性の経路印(which path marker)を付加しているため、経路印(which path marker)のない元の状態に戻すことが可能である。 経路印(which path marker)消去で通常の二重スリット実験に戻るから干渉縞が復活するのであって、経路情報(which path information)を消したことによって干渉縞が復活するわけではない。経路情報(which path information)を測定してしまうと、後からどうやろうとも、経路情報(which path information)を消去しようとも、干渉縞を復活させることはできない。

干渉縞が消失する場合について「波動性が消失する」と説明されることがあるが、これも間違っている。この実験で確認されたことは干渉縞の消失であって波動性の消失ではない。そして、この実験結果は、波動性を維持したままで説明可能な現象である。というか、波動性がある場合と条件が同じなのに波動性がなくなると考える理由がない。 波動性の有無についての検証は一切行われておらず、波動性が消失した証拠は一切ない。

実験方法

経路情報の付加

次の図のように、何らかのフィルター類を用いて、２つの経路を通過した後に経路印をつける。

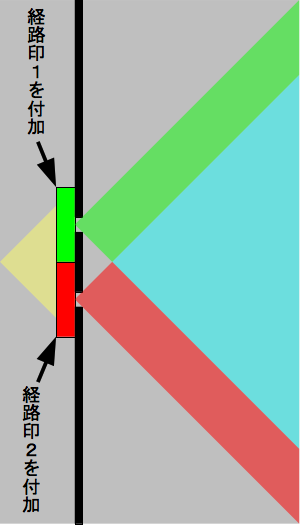
この経路印をスクリーン直前で検出すれば経路情報が得られる…というのが、スクリーン直前で経路情報を検出すると主張する理屈である。経路印を付加した場合は、実際に経路情報を測定しなくても干渉縞が消えるとされる。ただし、干渉縞が消えるだけであって、波の干渉がなくなるわけではない。

経路情報の消去

次の図のように、何らかのフィルター類を用いて、それまでに付加されていた経路印の内容に関わらず、いずれも同じ印が付加されるようにする。

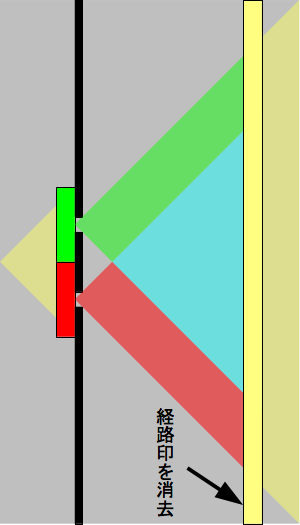
いずれも同じ印が付加されるということは、その印から経路を特定できなくなるので、経路情報を消去したに等しいと主張されている。この場合には、干渉縞が復活するとされる。

考察

経路印から経路情報を抽出可能か？

経路印から経路情報を抽出するためには、経路印の測定結果が片方のスリットのみの波動関数で決定されなければならない。

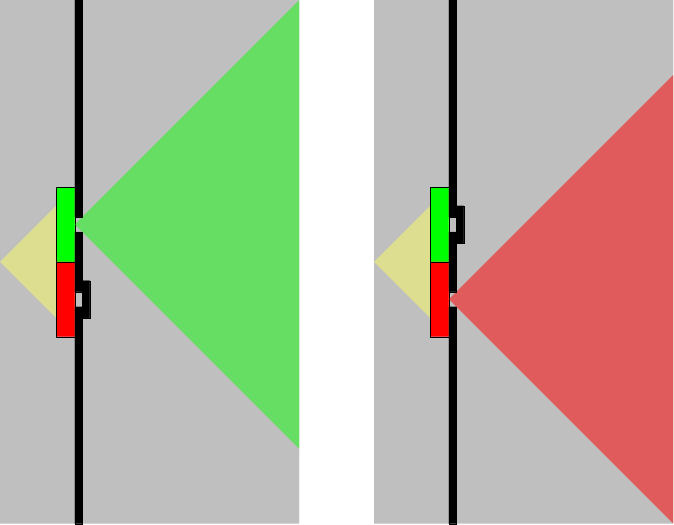
しかし、経路印を付加しただけでは、波動関数の経路を一方に制限する仕組みがないため、経路印から経路情報を抽出することは不可能である。

そして、可観測量は測定時点での波動関数によって決定される。 よって、可観測量の一種である経路印の測定結果は、両経路の波動関数の合成、すなわち、Ψ₁(x)+Ψ₂(x)によって決定される。 一方で、この経路印から経路を特定するためには、可観測量がΨ₁(x)かΨ₂(x)のいずれかによって決定されなければならない。 可観測量がΨ₁(x)かΨ₂(x)のいずれかによって決定されるならば、それは二重スリット実験としての条件が成立していないことを意味する。 二重スリット実験における経路を特定することを目的としているのだから、当然、この場合の可観測量はΨ₁(x)+Ψ₂(x)によって決定されなければならない。 だから、この実験では、経路印から経路情報を抽出することはできない。

干渉縞との関連性

一見すると、次のようにも見える。

経路印を付加すると干渉縞が消える
経路印を消去すると干渉縞が復活する

しかし、経路印なるものを付加しようとすれば、波のパラメータが変わるので、干渉結果に影響を与えるのは当然である。しかも、干渉縞が消える場合も、波としての干渉が失われるわけではない。後で説明する実験の「本格版」では直線偏光の偏光の向きとして、「簡易版」では円偏光か直線偏光か、及び、偏光の回転方向として干渉が生じる。そして、その干渉は綺麗に揃った模様となっているはずである。ただし、波の強度は干渉結果に関わらず一定となる。 通常の方法では、その干渉結果が視覚的に得られないから、干渉縞が観測できないだけに過ぎない。 二重スリット量子消しゴム検証実験の提唱に書いたようなやり方であれば、その干渉結果を視覚的に得ることが可能であろう。

もちろん、いくつかの仮定を置けば、経路印を付加した場合には、観測できない隠れた干渉縞はないという理論も構築可能である。しかし、そのような奇妙な仮定を置かなければならない合理的理由はないし、そのような奇妙な仮定の正しさを証明する根拠もない。であれば、オッカムの剃刀を適用して、そのような奇妙な仮定は棄却されるべきだろう。

つまり、経路印なるものを付加しようとしたことで、波のパラメータが変化し、その結果、干渉が波の強度変化以外に現れるようになっただけに過ぎない。 また、経路印なるものを消去しようとすると、さらに波のパラメータが変化し、その結果、また、干渉が波の強度変化に現れるようになる。 これは、経路印なるものが本当に経路印として機能しているかどうかとは関係がない。

そもそも、何の経路情報を知りたいのか？

二重スリット実験では、両方のスリットを通過した波がスクリーンに到達するので、スクリーン直前には両方の波の合成波が到達する。干渉縞が生じている以上、波が両方のスリットを通過したことは疑う余地がない。だから、波の通過経路を調べることには全く意味がない。両方のスリットを通過したに決まっているのだから、どちらのスリットを通過したか検出できるわけがないのである。通過スリットを調べることに意味があるのは、波ではなく粒子である。

では、この場合、スリットで経路印を付加する対象は、波なのか？それとも、粒子なのか？ 一般に、経路印として用いられるのは偏光であるので、経路印を付加する対象は粒子ではなく波となっている。それでは、このような経路印を付加する意味は全くない。

いずれにせよ、経路印を検出すれば経路情報を得られるという話は極めて疑わしい。 経路情報を得ることのできない見掛け倒しの経路印モドキを付加しているだけである。

原理まとめ

この方法は、隠れた変数理論の検証としては、役に立たない。というのも、隠れた変数理論の検証に用いるには、波が両経路を通過し、かつ、その波に影響を与えないよう、粒子の経路を特定する必要があるからである。

また、経路印を付加することと干渉縞の消失に因果関係があるのか、それとも、偶然そう見えるだけの現象なのかは、慎重に検討する必要があるだろう。

Double-slit quantum eraser（量子消しゴム実験）

一部で Double-slit quantum eraser (PHYSICAL REVIEW A, VOLUME 65, 033818) が話題になっているようだ。何も知らない素人が見ると「経路特定によって干渉が消失する」と誤読しかねない。 しかし、この実験結果では干渉消失の証拠は一つも示されていない。 むしろ、干渉があっても干渉縞が観測できない可能性、すなわち、干渉縞が観測できないことが干渉消失を意味しないことを示唆している。

実験セットの説明

基本実験装置

図（論文中のFIG.1）にも示されているように、D_Sを少しずつ(x)ずらした状態で何度もデータを取っているため、横軸をx、縦軸を検出数としたグラフを描くことが出来る。そして、このグラフが干渉パターンを描くかどうかが検証される。

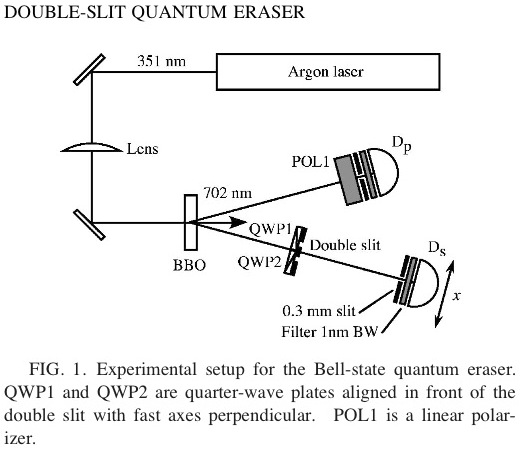
Double-slit quantum eraser (PHYSICAL REVIEW A, VOLUME 65, 033818)P.3

まず、POL1,QWP1,QWP2の全てがない状態では通常の二重スリット実験と同じとなる。よって、グラフは典型的な干渉縞パターンとなる（論文中のFIG.2）。

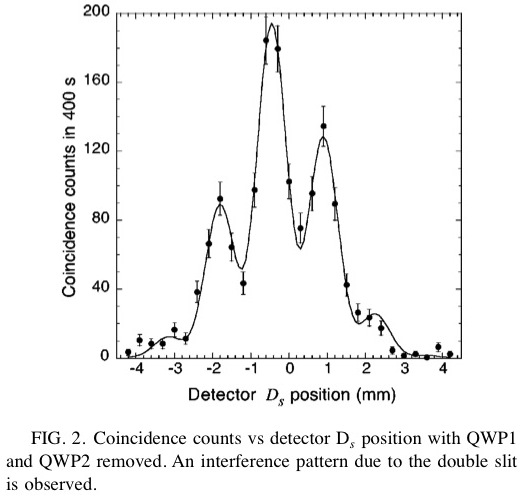
Double-slit quantum eraser (PHYSICAL REVIEW A, VOLUME 65, 033818)P.3

経路印(which path marker)を付加する実験セット

次の部分に実験セットの概要が説明されている。

Suppose that in front of each slit we place a quarter-wave plate, with the fast axis at an angle of 45° (􏰒or -􏰘45°)􏰀 with respect to the photon polarization direction.
各スリットの前に、光子の偏光方向に対して速軸(fast axis)が45°（または-45°）􏰀の角度で4分の1波長板を配置するものとする。
Double-slit quantum eraser (PHYSICAL REVIEW A, VOLUME 65, 033818)P.5

波長板 - 光学技研、wave plateによれば、wave platは垂直偏光と水平偏光で速度が変わる光学装置であって、quarter-wave plateは両偏光の位相シフトが1/4波長分(度数法では90°弧度法ではπ/2)となるwave plateを指す。偏波・偏光で説明した通り。直線偏光は2つのお互いに垂直な直線偏光に分解できる。この場合、速軸に並行な成分と垂直な成分に分けて考える。そして、quarter-wave plateを通過すると、速軸に垂直な成分が速軸に並行な成分より90°遅れる。 quarter-wave plateを通過した後は、位相シフト後の両成分を合成すれば良い。では、合成結果はどのようになるか。表計算ソフトを持っている人は散布図を書いてみると良い。

斜め線分の軌跡
- 横軸をcos
- 縦軸をcos
円の軌跡
- 横軸をcos
- 縦軸をsin
斜め線分の軌跡(先ほどと90°ずれ)
- 横軸をcos
- 縦軸を-cos
円の軌跡(先ほどと逆回転)
- 横軸をcos
- 縦軸を-sin

横軸を偏光の水平成分と縦軸を垂直成分と考えると、その位相関係を操作することで円偏光にしたり、直線偏光にしたりできることがわかろう。中間的な状況ならば楕円偏光にもなる。 quarter-wave plateの位相シフトは90°固定であるので、入ってくる偏光の向きにより、出力される偏光は次のように変わる。

0°入力なら出力は水平偏光
- 速軸がcos→cos
- 遅軸が0→0
45°入力なら出力は円偏光
- 速軸がcos/√2→cos/√2
- 遅軸がcos/√2→sin/√2
90°入力なら出力は垂直偏光(90°遅れ)
- 速軸が0→0
- 遅軸がcos→sin
-45°入力なら出力は円線偏光(先ほどと逆回転)
- 速軸がcos/√2→cos/√2
- 遅軸が-cos/√2→-sin/√2

ようするに、入ってくる偏光の向き次第で、出力される偏光がコロコロ変わる。以上で分からなくても、ネットで調べれば簡単に情報が見つかるだろう。例えば、Wikipedia:偏光の「波長板」の所では結論だけ書いてある。だから、ここではこれ以上は説明しない。

経路情報(which-path information)が得られるか？

この実験セットでどのようにして経路情報(which-path information)を得るかは次のように書いてある。

By looking at Eqs. (4),(8), and (9), it is clear that detection of photon s after the double slit with polarization R is compatible only with the passage of s through slit 1 and polarization L is compatible only with the passage of s through slit 2.
式(4),(8)および(９)を見れば、二重スリット後のｓにおける光子の検出において、偏光Ｒはスリット１の通過とのみ適合し、偏光Ｌはスリット２の通過とのみ適合することが明らかである。
Double-slit quantum eraser (PHYSICAL REVIEW A, VOLUME 65, 033818)P.4

D_Sの偏光の回転方向を検出すれば、経路情報(which-path information)が得られると書いてある。しかし、恐らく、この方法で経路情報(which-path information)を得ることは不可能であろう。何故なら、この実験では片方のスリットを通過した波のいずれか、すなわち、Ψ₁(x)かΨ₂(x)によって可観測量が決定されることを前提として経路情報(which-path information)が得られるものと扱っているが、それは量子力学の各種実験と整合しないからである。量子の可観測量は両方のスリットを通過した波の合成波、すなわち、Ψ₁(x)+Ψ₂(x)で決定されなければ、二重スリット実験の真相で説明した二重スリット実験やJ.Wheelerの遅延選択実験が説明できないからである。

D_Sに到達する直前の波は、Ψ₁(x)+Ψ₂(x)である。仮に、ここで、Ψ₁(x)とΨ₂(x)がそれぞれ逆回転の円偏光であるとしよう。ここで、両者の位相差をφとし、両者の中間の位相を基準にとると、次のように記述できる。

Ψ₁(x)
- 水平成分はcos(x+φ/2)
- 垂直成分はsin(x+φ/2)
Ψ₂(x)
- 水平成分はcos(x-φ/2)
- 垂直成分は-sin(x-φ/2)

これらを合成したΨ₁(x)とΨ₂(x)は次のとおりとなる。

水平成分は2cos(φ/2)cos(x)
垂直成分は2sin(φ/2)cos(x)

これはφによって偏光の向きが決まる直線偏光である。そして、これは逆回転の円偏光の等量の合成である。仮に、Ψ₁(x)+Ψ₂(x)を何らかの方法で2つの逆回転の円偏光に分解したとしても、それらがそれぞれΨ₁(x)とΨ₂(x)と一対一で対応しているとは限らない。 というか、両者を区別なく合成されたΨ₁(x)+Ψ₂(x)からΨ₁(x)とΨ₂(x)を分離抽出することは不可能である。

たしかに、可観測量がΨ₁(x)かΨ₂(x)のいずれかによって決定されているならば、検出結果は経路情報(which-path information)となろう。 しかし、Ψ₁(x)+Ψ₂(x)で可観測量が決定されていれば、偏光の向きを測定しても経路情報(which-path information)を得ることはできない。 円偏光の回転方向を測定したなら、測定結果は直線偏光のうちの片方の回転方向の円偏光成分が取り出されたと解釈できるのだか、それぞれの成分がΨ₁(x)かΨ₂(x)で決定されたとする根拠はない。 何故なら、検出された円偏光成分は、どちらも、Ψ₁(x)とΨ₂(x)のそれぞれの一部が合成されたものと考えても辻褄が合うからである。 例えば、測定結果がΨ₁(x)と同じ回転方向だった場合、検出された光は次の2つの合成である可能性がある。

Ψ₁(x)の垂直成分
Ψ₂(x)の水平成分

逆に、測定結果がΨ₂(x)と同じ回転方向だった場合、検出された光は次の2つの合成である可能性がある。

Ψ₁(x)の水平成分
Ψ₂(x)の垂直成分

だから、円偏光を測定しても、Ψ₁(x)かΨ₂(x)のいずれかを検出した、とは保証されない。

可観測量がΨ₁(x)かΨ₂(x)のいずれかのみによって決定されるためには、ランダムにどちらかの経路を塞いだ事実上の単一スリット実験(以下、「ランダム単一スリット実験」)にするしかない。 つまり、検出結果が経路情報(which-path information)となるためには、二重スリットの前提が崩れることを必要とする。 言い換えると、二重スリットの前提が維持される場合は、検出結果が経路情報(which-path information)となる可能性は否定される。 また、もしも、二重スリットの前提がくずれるなら、どのような細工をしようとも干渉縞は復活しないはずである。しかし、この実験では、D_P直前に挿入する偏光板の向き次第で干渉縞は復活する。これは、二重スリットの前提が成立していないと説明がつかない。

繰り返すが、二重スリットの条件を維持しなければ、経路情報(which-path information)を得る意味がない。だから、もしも、検出した偏光の回転方向が経路情報(which-path information)であるとするなら、それを実験で証明する必要がある。でなければ、それは経路情報(which-path information)として意味を持たない、ただのランダムなデータに過ぎない。

干渉について

POL1なしにQWP1とQWP2を置くと、何故、干渉縞が消えるのか。 BBO(β-メタホウ酸バリウム)に入射した光は、タイプⅡの自発的パラメトリック下方変換により、2方向の光に分解される。この時、どちらの方向も直線偏光となるが、出力される偏光の向きはランダムであり、2方向の光の偏光の向きがお互いに垂直の関係になる。 BBOから出力された光は1/4波長板に入力される。 1/4波長板に入力される偏光の向きの影響は、先ほど説明したとおりである。

0°入力なら出力は水平偏光
- 速軸がcos→cos
- 遅軸が0→0
45°入力なら出力は円偏光
- 速軸がcos/√2→cos/√2
- 遅軸がcos/√2→sin/√2
90°入力なら出力は垂直偏光(90°遅れ)
- 速軸が0→0
- 遅軸がcos→sin
-45°入力なら出力は円線偏光(先ほどと逆回転)
- 速軸がcos/√2→cos/√2
- 遅軸が-cos/√2→-sin/√2

そして、1/4波長板は左右で90°ずらして設置している。そのため、1/4波長板の入力光の偏光が速軸と45°ずれている場合は、お互いに逆向きの円偏光となる。お互いの逆向きの円偏光の干渉結果は、偏波(偏光)方向のみに影響し、波の大きさ(光の強さ)には影響しないため、干渉縞は現れない。また、1/4波長板の入力光の偏光が速軸と一致する場合に比べて、速軸と垂直な場合は1/4波長相当(90°)の位相遅れが生じる。そして、位相遅れが生じる方のスリットは、入力光の偏光とQWP1のfast axis(速軸)の角度が0°の場合と90°の場合で逆になる。その結果、入力光の偏光とQWP1のfast axis(速軸)の角度が0°の場合と90°の場合では、干渉縞が逆パターンとなる。それらを図にすると次のようになる。

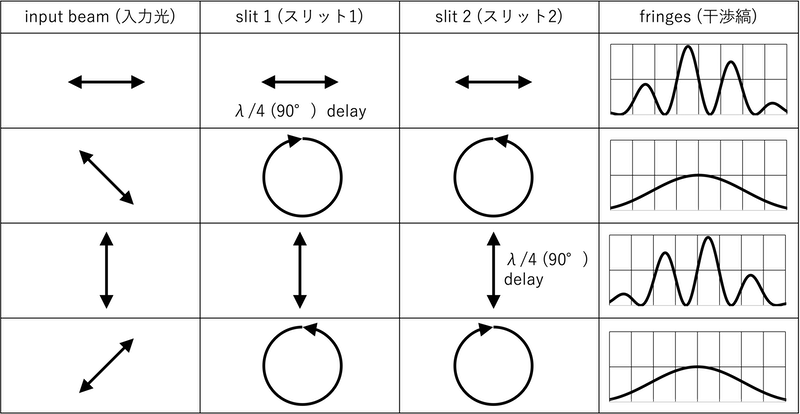
これらを平均化すると、ちょうど干渉縞が打ち消しあって消えてしまう。定量的には一回転分の積分をしないと正確なことは言えないが、何となく逆パターンの干渉縞が等量で混じり合って打ち消し合うことは理解できると思う。つまり、POL1なしにQWP1とQWP2を置くだけなら、干渉そのものが発生しないわけではなく、干渉縞として現れないだけである。

もちろん、いくつかの仮定を置けば、POL1がない場合には干渉そのものが発生しないという理論も構築可能である。しかし、そのような奇妙な仮定を置かなければならない合理的理由はないし、そのような奇妙な仮定の正しさを証明する根拠もない。であれば、オッカムの剃刀を適用して、そのような奇妙な仮定は棄却されるべきだろう。

QWP1とQWP2の他にPOL1を置くことで干渉縞が復活するのは、「Coincidence counts (一致する計数)」故の現象である。図のBBO(β-メタホウ酸バリウム)に入射した光は、タイプⅡの自発的パラメトリック下方変換により、お互いに垂直な向きの2方向の光に分解される。そのために、D_S側とD_P側に向かう偏光の向きは90°ずれた関係となる。だから、偏光の向きが固定された場合のD_P側の測定結果と「Coincidence counts (一致する計数)」すると、それは、D_S側に向かう光のうちの特定の偏光の場合の結果のみを抽出することとなる。先の表を見てわかる通り、D_S側に向かった光の偏光とQWP1のfast axis(速軸)の角度によって、干渉縞が生じたり生じなかったりする。

つまり、POL1の向きによってQWPの入力光のうちの特定の向きの偏光の結果のみが抽出されることで、その向きに応じた干渉パターン(干渉縞なしの場合も含む)が抽出される。厳密に言えば、偏光板では特定の向きの偏光の結果だけを取り出すことはできない。偏波・偏光で説明した通り、偏光の向きと偏光板の角度をθとすると、偏光板通過後の振幅はcosθ倍となる。検出確率は振幅の2乗に比例するから、偏光板通過後の検出確率はcos²θに比例する。 θが０°の時の検出率が100％なら、θが90°の時の検出率は０％となる。ようするに、特定の向きの偏光に近いほど高い確率で結果を抽出するに過ぎない。その結果、抽出される干渉縞は若干ボヤける。

尚、BBOではなくKDPを(リン酸二水素カリウム)を使った場合は、タイプⅠの自発的パラメトリック下方変換となって、お互いに平行な向きの2方向の光に分解される。結果が90°ずれる以外はBBOの場合と同様である。

量子消しゴムの条件

この実験では、経路情報(which-path information)を測定していないから、経路情報(which-path information)を後から消したとは言えない。とはいえ、量子消しゴム(quantum eraser)と名乗るからには、少なくとも何らかの情報等を後から消す必要がある。しかし、この実験では先の表のいずれかの結果を分離抽出したに過ぎない。

すなわち、経路印(which path marker)を付加した場合の結果と付加しなかった場合の結果を分離抽出したに過ぎない。経路印(which path marker)を付加した場合において、経路印(which path marker)を後から消す操作を行なっていないのである。よって、この実験は量子消しゴム(quantum eraser)の条件を満たさない。

まとめ

既に説明した通り、この実験には次の２点の問題点がある。

この実験における経路印(which path marker)は経路情報(which-path information)として機能していない疑いが強い
この実験はあらかじめ付加した経路印(which path marker)を測定前に破棄するという量子消しゴム(quantum eraser)の条件を満たしていない

また、経路印(which path marker)の有無と干渉縞の有無の関係も従来理論に基づいた考察で十分に説明が可能である。あたかも経路印(which path marker)を付加した場合だけ干渉縞が消えるかのようにも見えるが、たまたまそのようになったのか、あるいは、そうなる必然性があったのかは、この実験結果からは知りようがない。よって、この実験結果から、経路印の付加と干渉消失の因果関係を推定することは不可能である。この実験の肝は次の一文に集約される。

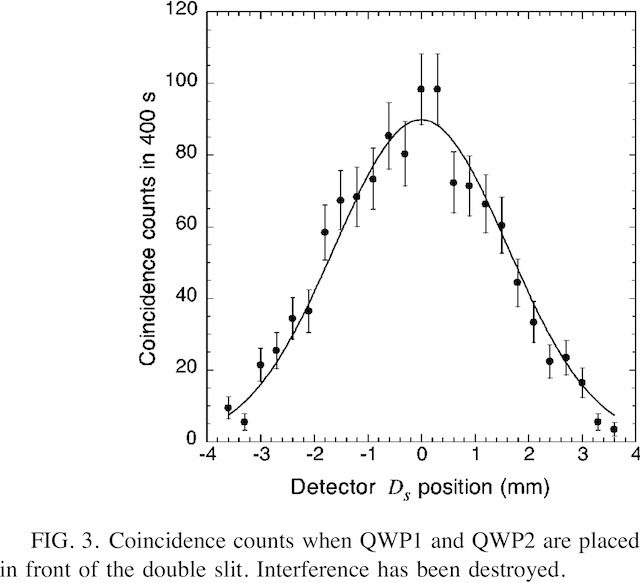
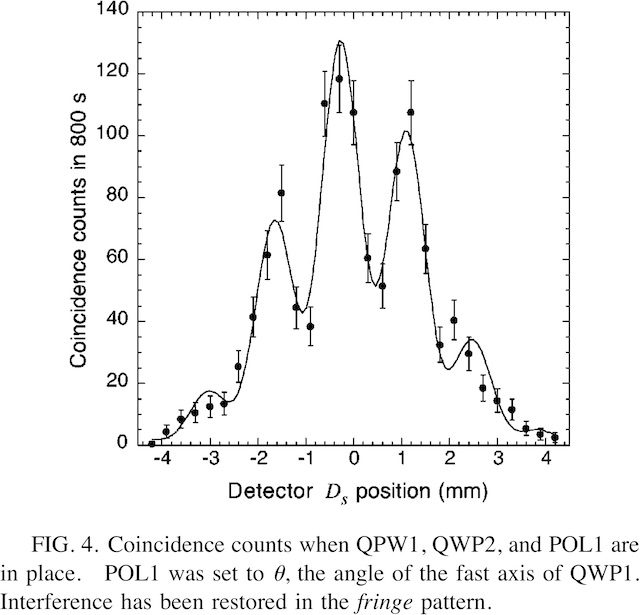
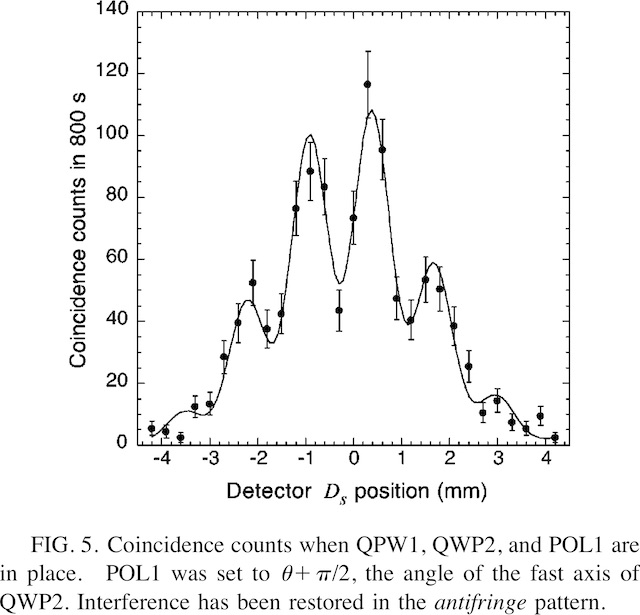
The averaged sum of these two interference patterns gives a pattern roughly equal to that of Fig. 3.
これら２つの干渉縞(Fig .4とFig .5)の平均は、Fig. 3とほぼ等しいパターンを与える。
Double-slit quantum eraser (PHYSICAL REVIEW A, VOLUME 65, 033818)P.3-5

これは、二種類の干渉縞が相殺しあって干渉縞が消失した可能性を示唆している。 すなわち、干渉縞が観測できないことは干渉がない証拠にはならないという至極当然のことを示唆している。

先にも説明した通り、いくつかの仮定を置けば、POL1がない場合には隠れた干渉縞はないという理論も構築可能である。しかし、そのような奇妙な仮定を置かなければならない合理的理由はないし、そのような奇妙な仮定の正しさを証明する根拠もない。であれば、オッカムの剃刀を適用して、そのような奇妙な仮定は棄却されるべきだろう。

尚、二重スリット量子消しゴム検証実験の提唱に経路印(which path marker)が経路情報(which-path information)として機能しているかの検証実験の具体的方法を提唱している。

簡易版？

ちなみに、この実験の「簡易版」とやらでは偏光面が直交することにより、干渉結果が波の大小に影響しなくなる。コメント欄に書かれているように、偏光板が偏光面の直交性を生むことによって、干渉縞が消えている。なお、そこに書かれている科学的誤りは二重スリット量子消しゴム実験トンデモ解説に移動した。

誤った説明の例

誤った説明の事例は二重スリット量子消しゴム実験トンデモ解説に移動した。

「簡易版」とやらの間違い
ニコニコ動画の間違い
河合塾による疑似科学紹介

このページの参照元
科学意識解釈遅延選択量子消しゴム実験二重スリット実験の真相二重スリット量子消しゴム実験(旧) 二重スリット量子消しゴム実験トンデモ解説二重スリット量子消しゴム検証実験の提唱