確率力学

• はじめに
• エドワード・ネルソンの確率力学

はじめに 

ここでは量子力学の隠れた変数理論の一種である二重解の理論の派生形について紹介する。

エドワード・ネルソンの確率力学 

エドワード・ネルソンは粒子がブラウン運動をすると仮定した隠れた変数理論を発表した。

ボームの量子ポテンシャル理論の発展型とみなせる理論の1つに,ボームと同じプリンストン大学のE.ネルソンが1966年に発表した確率力学がある。

---

数式の展開の詳細はやや複雑なので文献17,22)に譲るが,ネルソンは,(18)式で記述される確率過程の式から,見事,シュレーディンガー方程式を導いた。 これは,「ランダムにジグザグ運動する粒子」を想定すれば,個々の粒子の波動性をあらわに考慮せずとも,後述のように,標準的な量子力学と矛盾することなく,観測される粒子と波動の二重性が解釈できるということである。 理論物理学者の並木美喜雄は,ネルソンの仕事を,「量子力学のブラウン運動論的解釈を完成させた見事な理論」と評価し,「説明学的な面白さ」を認め,「量子力学の内容理解を深めたことは間違いない」としている。

ここで,「電子がブラウン運動をしている」ことは,「運動がなめらかではない」ことを意味しているのに気づく読者もいるだろう。 なめらかでない運動=ジグザグ運動は,一般に微分で表すことができない。 シュレーディンガーがシュレーディンガー方程式を導出した時代には,微分不可能な関数を扱える数学(確率解析学)が十分発達していなかった。 ネルソンの成功の裏には,確率解析学の発達があった。 これを量子力学に上手く応用することで,シュレーディンガーが到達しえなかった「電子のブラウン運動的な動き」にネルソンは到達できたのである。

---

我々のような量子力学の入門者が,確率力学を学ぶ時にどうしても気になるのが,上記の「問題点1」に関係する,「真空中の電子がブラウン運動することを支持する証拠はあるのか?また,あるとしたら,電子にブラウン運動を起こさせる実体は一体何なのか?」ということである。 前述の通り,確率力学は,それらの疑問に答えない。 確率力学はただ,「電子がブラウン運動をすると仮定すると,シュレーディンガー方程式が導けること」を示すだけである(これだけでも相当すごいが)。 ネルソン自身は,(おそらく皮肉もこめて)「エーテル」の概念にふれている。 一方,確率力学の研究者,長澤正雄は,「こだわる必要はない」と前置きしながら,「真空では目にとまらない非常に短い時間に粒子が生まれたり死んだりしている。この生まれたり死んだりがノイズ(電子のジグザグ運動)の原因だと考えることもできる」と述べている。

教育ノート１．波動関数のわかりやすい説明 - 日本女子大学紀要 理学部 第24号(2016)P.13,15

---

量子が不確定性原理により支配されているならば、その運動は滑らかではないはずである。 従って、量子の運動は本来、微分不可能と考えられる。Schrödinger方程式が微分方程式で記述されているのは、量子の統計的性質を表す式だからである。 個々の量子を記述するためには、微分不可能な変数を扱える確率解析学が不可欠と考えられる。 余談であるが、確率解析学の応用範囲は実に広い。 有名なものには、ノーベル経済学賞を受賞したブラック‐ショールズ理論がある。 その他にも、生物学、化学、物理学それに原子力工学と多岐にわたる。 そして量子力学に応用されたのが確率力学である。

---

すなわち、確率微分方程式(21)の平均前方速度場b(及び確率微分方程式(25)の平均後方速度場b*)を決定する“古典力学的な”Newton-Nelson方程式(23)は、Schrödinger方程式なのである。 確率力学も標準的な量子力学と矛盾することはない。

量子ポテンシャル理論と確率力学 - 核データニュース，No.76(2003)P.42-46

しかし、ネルソンは、粒子の軌道を前提とした理論を構築しようとしたわけではない。

ヒルベルト空間における作用素の数学を専門としていたネルソンは，1960年代前半に量子力学を電磁場などの場にあてはめた「場の量子論」の公理化の研究をおこなっていた。 そこでは場の量子論が抱えていた様々な問題点を克服するために，確率論の数学的枠組が利用されていた。

---

このような場の量子という概念は，様々な素粒子が衝突反応によって別種の素粒子を生成したり消滅させたりする現象を記述するのに適しているため，主に素粒子論において多用されていた。 つまり素粒子は場の量子に他ならないとするのだ。

しかしながら，空間の各点に与えられるため空間全体では無限個の調和振動子が存在することによる根本的な問題点もあった。 例えば，空間のどこにも何も素粒子が存在しない状況は真空に他ならないが，場の量子論では空間の全ての点の調和振動子がエネルギーの最小値ħ/2を持つため，それが無限個ある全体では ħ/2＋ħ/2＋ħ/2＋……＝∞ となって，何もない真空が無限大のエネルギーを持つことになってしまう！

問題はこれだけではない。

空間の各点にある調和振動子の変位やエネルギーといった物理量は，例えば無限行無限列の行列あるいはヒルベルト空間の作用素として定められるが，場の物理量としては全ての点での物理量をまとめたものとなり，行列や作用素の無限個の組み合わせを考えなければならない。 ところが，そのような無限個の組み合わせを数学的に矛盾なく作り出すことはできないということが見いだされていた。

つまり，行列力学や波動力学を無限個の調和振動子の集まりと見なした場に適用するのは，数学的な問題が多くなることがはっきりとしてきたのだ。 そこで多くの物理学者は残された量子力学の枠組としてのファインマンの経路積分を場にあてはめる研究に向かっていった。

しかし，１個の調和振動子のときでさえ無限重積分を必要とした経路積分の技法は，実は数学的には正当化できないものだった。 それは，ファインマンが用いた無限重積分は存在しないことが容易に示されるからだ。 そのようなものを，さらに場に適用するためには無限個の無限重積分までも持ち出さなくてはならず，問題はより大きくなってしまう。

それでも他に方法がなかったため，理論物理学者たちは「赤信号，皆で渡ればこわくない」の標語どおり，たとえ数学的にはまちがった経路積分の式であろうとも，全員で場の量子論の枠組として使っていたのだ。

しかし，数学者としての良心に忠実だったネルソンは，何とかしてファインマンの経路積分を数学的に正しい形に整備し，その上で場の量子論にあてはめようと考えていた。 同時に，経路積分には結局は用いられなかった最小作用の法則が，うまくいけば復活する可能性もあると期待していた。

「Excelで学ぶ量子力学〜量子の世界を覗き見る確率力学入門〜」(ISBN-10:4062573474,ISBN-13:978-4062573474,著:保江邦夫)P.64〜66

ネルソンは、場の量子論を数学的に厳密なものにしようとした結果、粒子がブラウン運動をすると仮定した隠れた変数理論に到達したのである。 そして、その元になった経路積分も粒子の軌道を前提とした理論を構築しようとしたわけではない。

ジョークで「ビールを飲んでる」と答えてから，ファインマンは自分が抱えている大問題の糸口を求め，逆にこんな質問をあびせたのだ。

「行列力学や波動力学のようにハミルトニアンを含む微分方程式から出発するのではなく，ラグランジアンについての最小作用の法則から出発する量子力学を知りませんか？」

---

「最小作用の法則は出てこないが，しかし少なくともラグランジアンが出てくる量子力学についての論文をディラックが書いている」

---

ディラックの論文には，確かにラグランジアンが登場してきてはいたが，残念ながらファインマンが求めていたような最小作用の法則から出発して量子力学を与えるものではなかった。 ただ，波動力学における波動関数が時間とともに変化していく様子をごく短時間で見ると，そこにはラグランジアンが出てくるという事実を記したものだった。

「Excelで学ぶ量子力学〜量子の世界を覗き見る確率力学入門〜」(ISBN-10:4062573474,ISBN-13:978-4062573474,著:保江邦夫)P.52,55

量子力学以外の物理法則は、悉く、「ラグランジアンについての最小作用の法則から出発する」ことによって導出されている。 だから、ファインマンは、法則の導出過程において古典力学への回帰を目指したと言って差し支えないだろう。 しかし、特定の結論に導こうとしたわけではないので、隠れた変数理論を目指したわけでも、粒子軌道に固執したわけでもない。

以上の理論の構築過程を見れば、ネルソンの確率力学が二重解の理論を元にした理論でないことは明らかである。 だから、ネルソンの確率力学を二重解の理論の派生形として扱うことには異論もあろう。 しかし、結果的に、ネルソンの確率力学でも、二重解の理論と同様、運動方程式に従う粒子とその運動方程式を決める波動関数という枠組みは踏襲されている。 だから、結果だけ見れば、ネルソンの確率力学は二重解の理論の派生形になっていると言っても過言ではない。

二重スリット実験の真相で説明した通り、二重スリット実験における粒子の軌跡は確率力学では次のようになる。

では,確率力学は,二重スリット実験をどう説明するのであろうか? 確率力学から得られる電子の軌跡は,大まかにいって,量子ポテンシャルが与える軌跡をジグザクに揺動しながら進むというものである。 よって,量子ポテンシャルから得られる結果は,およそ保持される。 つまり,確率力学でも,電子はどちらか一方のスリットしか通らない。 そして,線源から見て左側のスリットを通ったものはほぼスクリーンの左側に到達し,右側のスリットを通過したものスクリーンの右に到達する。 ただし,2つの理論間には違いもある。 たとえば,確率力学では,電子のジグザグ運動のため,中央付近に進んだ電子は,左右が入れ替わることもある。 このことが示唆するように,ボームの量子ポテンシャル理論では,電子がたどる軌跡が決まれば,スクリーンのどこに到達するかは一意的に決まるが,確率力学では電子の揺動のため,一意的に決まらない。 このように,確率力学は,量子ポテンシャル理論よりも,不確定性が大きな理論である。

教育ノート１．波動関数のわかりやすい説明 - 日本女子大学紀要 理学部 第24号(2016)P.14

---

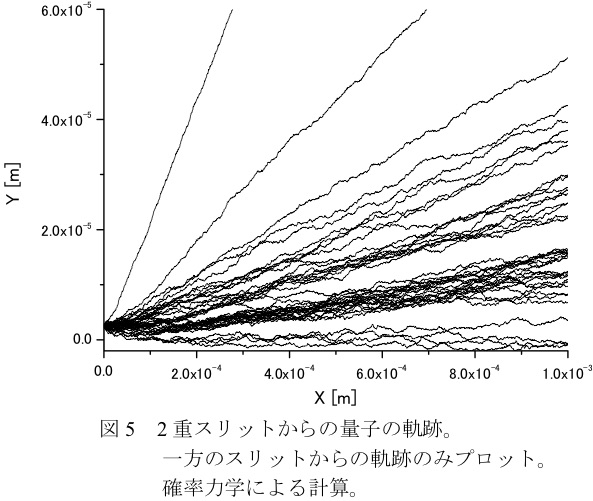
この図でも線源から見て左側のスリットからのみの軌跡を示した。 量子ポテンシャル理論の場合(図2参照)と異なり、軌跡全体が量子揺らぎを示している。 しかしながら量子ポテンシャル理論の場合と同様に、線源から見て左側のスリットを通過した量子はスクリーンのほぼ左側に到達する。 量子ポテンシャル理論では厳密にスクリーンの左側であったが、確率力学では中央の0次干渉ピーク近傍であればスクリーンの右側にも到達する。

---

またスリット内での量子の通過位置が決まれば、量子ポテンシャル理論ではスクリーン上での位置は一意的に決まるが、確率力学では干渉ピークをまたがって分布し一意的には決まらないのも、両理論の差異である。

量子ポテンシャル理論と確率力学 - 核データニュース，No.76(2003)P.46,47

確率力学の課題が次のように指摘されている。

大まかに言って,確率力学は,ボームの量子ポテンシャルを,「ブラウン運動する電子の(空の)軌跡」とおきかえて,量子力学を組み直したものなので,前述のボームの理論の問題点1,3,4は未解決のまま残される。 すなわち,量子ポテンシャルがそうであったように,確率力学それ自身は,「電子のブラウン運動」をもたらす原因を明らかにしない。 しかし,これについては,重要な傍証があるので,6章であらためて議論する。 また,ボームの理論同様,確率力学が最終的に与える計算結果(=実験と比較可能な結果)は,標準的な量子力学と同じものである。 電子のブラウン運動的な軌跡は,実際には観測できない。ボームの理論の最大の難所16)であった「非局所性」もそのままである。

教育ノート１．波動関数のわかりやすい説明 - 日本女子大学紀要 理学部 第24号(2016)P.14

量子ポテンシャル理論が標準理論と比べて唯一劣っている点は「束縛状態の電子状態に実験とあわない点がある」ことだけである。 それを確率力学が解決できているなら、標準理論と比べて劣る点はないことになる。

尚、井元信之氏は、 決定論的量子力学? ボーム理論はどこまで行くか?(大阪大学基礎工学研究科 井元信之) - 高知工科大学 にて、局所性の制限はブラックボックスの外からのaccessible(アクセス可能)な現象のみに適用されるのであって、ブラックボックスの外からのaccessible(アクセス可能)でない所で非局所性が現れても相対性理論には反しないとしている。